49 Билет

Существование первообразной у любой непрерывной функции.

В данном параграфе мы будем рассматривать интеграл вида , где подынтегральная функция определена и интегрируема на некотором сегменте , а - произвольная точка сегмента . Определим на сегмента функцию

теорема 3.1. Пусть функция непрерывна на сегменте , тогда функция , определённая равенством (1), дифференцируема в каждой точке x сегмента , при этом

Доказательство. Пусть x произвольная точка сегмента . Тогда

Согласно формуле среднего значения

где

Учитывая равенство (4) в равенстве (3), получим

Пользуясь непрерывностью функции в точке и тем, что , из равенства (5) получим, . Теорема 1.1 доказана.

Замечание. Из теоремы 3.1 следует, что для непрерывной на сегменте функции функция является одной из первообразных. Тогда, в силу следствия из теоремы 1.1, гл.8, любая первообразная функции будет иметь вид .

§4. Основная формула интегрального исчисления.

1. Формула Ньютона-Лейбница.

Пусть функция непрерывна на сегменте , тогда, в силу теоремы 3.1 для любой точки , функция

является одной из первообразных функции . В частности, взяв в качестве точки точку , получим, что и функция является первообразной функции .

Теорема 4.1. Пусть функция непрерывна на сегменте и - любая первообразная функции на этом сегменте, тогда

Доказательство. Так как является одной из первообразных функции на сегменте , то, в силу теоремы 1.1 главы 8, первообразную функцию можно представить в виде

где - некоторая постоянная. Пользуясь равенством (2), вычислим .

Тем самым справедливость формулы (1) доказана.

Формула (1) называется формулой Ньютона-Лейбница.

Пользуясь обозначением

формулу Ньютона-Лейбница можно записать в виде

2. Замена переменной в определённом интеграле.

Теорема 4.2. Пусть функция непрерывна на сегменте , а функция дифференцируема на сегменте , причём производная непрерывна в каждой точке сегмента . Пусть множеством значений функции является сегмент и при этом

, тогда справедлива формула

Доказательство. Пусть F(x) – какая-нибудь первообразная функции на сегменте ; тогда по формуле Ньютона-Лейбница

Рассмотрим функцию , определённую на сегменте . Согласно правилу дифференцирования сложной функции

Отсюда следует, что функция является первообразной для функции , непрерывной на сегменте , и поэтому, согласно формулк Ньютона-Лейбница, получим

Теорема доказана.

3. Формула интегрирования по частям в определённом интеграле.

Теорема 4.3. Пусть функции и имеют непрерывные производные на отрезке , тогда справедлива формула

Доказательство. Так как функция является первообразной для функции

, то, согласно формуле Ньютона-Лейбница

Из равенства (7) найдём

Теорема 4.3 доказана.

Учитывая справедливость равенств формулу (6) можно записать в более компактной форме:

50 Билет

Несобственный интеграл первого рода.

Пусть функция определена на множестве и интегрируема на любом сегменте . Тогда, если существует конечный предел

то этот предел называется несобственным интегралом первого рода и обозначается символом

Таким образом, по определению

В случае, когда существует конечный предел , интеграл называется сходящимся, в противном случае расходящимся.

Аналогично интегралу (1) вводится несобственный интеграл по промежутку

Наконец, несобственный интеграл с двумя бесконечными пределами

определяется как сумма двух несобственных интегралов и , где – любое действительное число, при условии существования обоих несобственных интегралов, т.е.

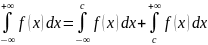
В качестве примера вычислим несобственный интеграл

Рассмотрим два случая.

1) . Пользуясь определением несобственного интеграла I рода,

2) Если , легко убедиться, что расходится. Следовательно, сходится при и расходится при .