ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Ростовский государственный экономический университет

( Р И Н Х )

СИТНИКОВ Р.В. 

 

СИСТЕМНЫЙ АНАЛИЗ В УПРАВЛЕНИИ

ОРГАНИЗАЦИЕЙ

П Р А К Т И К У М

Ростов-на-Дону

2008

УДК 658.351/ 303.732

Ситников Р.В. Системный анализ в управлении: Практикум. – Ростов н/Д: РГЭУ, 2008. - 50 с.

Практикум содержит задания по учебной дисциплине "Исследование систем управления" для индивидуальной и групповой работы студентов, обучающихся по специальности 080507 "Менеджмент организации", и в магистратуре по направлению 080500 "Менеджмент", на практических занятиях и во время самостоятельной подготовки, а также примеры решения типовых задач.

Набор задач и заданий соответствует требованиям рабочей программы учебной дисциплины 2008 года и требованиям государственного образовательного стандарта к навыкам применения методологии системного подхода для решения сложных задач управления. По содержанию, основным понятиям и условным обозначениям задачи практикума ориентированы на материалы по дисциплине [1, 4, 5, 13].

Рецензенты: к.э.н., профессор Рудский А.А. (РГЭУ),

д.т.н., профессор Золотухин В.Ф. (РВИРВ).

Утверждено в качестве практикума редакционно-издательским

советом РГЭУ.

© - Ситников Р.В., 2008

© - Ростовский государственный экономический

университет, 2008

Содержание

1 Общие задачи системного анализа . . . . . . . . . . . . . . . . . . . . . . . .	4
2 Задачи на основе вероятностных моделей . . . . . . . . . . . . . . . . .	24
3 Задачи частично структурированных моделей . . . . . . . . . . . . .	35
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	42
Приложения
Приложение А Основные формулы …………………………….	43
Приложение Б Ответы к задачам ……………………………….	44
Приложение В Примеры вопросов для тестового контроля ….	46
Приложение Г Деловые игры . . . . . . . . . . . . . . . . . . . . . . . . . . . .	48

Общие задачи системного анализа

Задача 1.1. Представить в виде системы РГЭУ(РИНХ), выделив основные подразделения и органы системы управления, вспомогательные подразделения. Дать общую оценку видов структуры управления учебно-воспитательным процессом, перечислить основные задачи организации и проблемы развития на современном этапе.

Задача 1.2. Представить в виде системы факультет, выделив основные подразделения и органы системы управления, вспомогательные подразделения. Дать качественную и количественную оценку структуры управления учебно-воспитательным процессом, перечислить основные задачи организации и проблемы развития на современном этапе.

Задача 1.3. Представить в виде системы выпускающую кафедру, перечислить основные решаемые задачи. Дать качественную и количественную оценку структуры управления учебно-воспитательным процессом.

Задача 1.4. На основе системного подхода провести анализ состояния системы водоснабжения в г. Ростов-на-Дону.

1. Среди множества проблем и целей функционирования системы водоснабжения выделим одну: низкое качество воды.

2. Цель анализа: обеспечить качество воды в соответствии со стандартами.

3. Задачи: обеспечить состав воды с показателями а) количество механических примесей не более 0,1 г на литр, б) концентрация углеводородных примесей не более 0,8 %, остальные показатели по ГОСТ.

4. Ограничения: 1) расход воды не менее 200000 куб. метров в сутки, 2) затраты на достижение цели не более 100000 у.е., 3) расширение территории очистных сооружений невозможно.

5. В 2003 году мэрия города обсуждала программу “Чистая вода”. Предлагалось четыре проекта (варианта доработки системы водоснабжения):

S1 – модернизация отстойников с увеличением их ёмкости,

S2 – врезка дополнительных фильтрующих блоков в водоводы,

S3 – установка систем доочистки воды в учреждениях и жилых домах,

S4 – наладить собственное производство расфасованной воды.

6. Для сравнительной оценки этих проектов специалисты предложили пять критериев:

К1 – количество получаемой воды,

К2 – затраты на реализацию проекта,

К3 – время на реализацию проекта,

К4 – технологический уровень доработок,

К5 – эксплуатационные расходы после реализации проекта.

7. Далее необходимо рассчитать значения критериев (или их приоритет) по каждому проекту, определить значимость каждого критерия (их весовые коэффициенты) и принять решение о наиболее эффективном проекте.

Задача 1.5. Провести анализ загрузки структурных подразделений при выполнении фирмой ряда функций. В фирме есть три структурных подразделения S1, S2, S3, которые выполняют четыре функции (работы) F1, … F4.

Последовательность анализа:

1. составить таблицу распределения подразделений при выполнении соответствующих функций (таблица 1.1);

Таблица 1.1 – Отношения подразделений и функций в системе

Подразделения	Функции				Всего Fj
	F1	F2	F3	F4
S1		1			1
S2	1	1	1		3
S3	1	1	1	1	4
Всего Si	2	3	2	1

2) определить занятость структурных подразделений при выполнении рассматриваемых функций; показать общую трудоёмкость подразделений и выполняемых функций;

3) определить объём выполняемых операций в часах;

4) определить среднюю производительность в структурах и сделать вывод о загруженности подразделений относительно нормативов.

Задача 1.6. На трех участках фирмы обрабатывается два вида деталей. Известна загрузка каждого участка (в процентах) при обработке одной детали и прибыль от реализации одной детали. Требуется определить, сколько деталей каждого вида следует обрабатывать при возможно полной загрузке участков, чтобы получить максимальную прибыль. (Возможны и другие ограничения: по расходу материалов, заработной плате, максимальному времени на изготовление и т.д.).

Задания для анализа процесса управления: определить изменения в плане выпуска деталей, если изменится допустимая загрузка участков общая или по отдельным деталям, цена деталей.

Таблица 1.2 – Данные к задаче 1.6

Деталь	Загрузка участков, %			Прибыль от одной детали, рубли
	№ 1	№ 2	№ 3
Д 1	5	3,3	2	120
Д 2	4	6,4	7	160
Максимальная загрузка участков, %	100	100	100

Задача 1.7. На фирме имеется запас сырья (150 тонн) и рабочей силы (390 чел./час). Планируется производства двух видов продукции: расход сырья 3 и 5 тонн соответственно, трудозатраты 13 и 10 чел./час. Ожидаемая прибыль на единицу продукции 32 и 36 тыс. рублей на единицу продукции 32 и 36 тыс. рублей.

Необходимо рассчитать:

1. План выпуска продукции типа А и Б, обеспечивающий максимальную общую прибыль.

2. Прирост прибыли при увеличении запаса сырья на 10 тонн.

3. Снижение прибыли при уменьшении ресурса трудозатрат на 10%.

4. Изменение плана и прибыли при изменении запаса сырья на 1 тонну.

5. Изменение плана и прибыли при изменении ресурса трудозатрат на 1 час.

Таблица 1.3 - Исходные данные

	Расход ресурса		Запас ресурса
	продукт А	продукт Б
Сырье, т	3	5	150
Трудозатраты, ч	13	10	390
Прибыль на ед. продукта, тыс руб/т	32	36

Задача 1.8. Менеджер должен решить, сколько упаковок краски каждого из двух типов следует изготовить, чтобы получить максимальную прибыль. Ограничения по ресурсам (таблица 1.4):

• общее время работы оборудования 30 часов,

• на складе имеется исходных реагентов вида А – 100 кг, вида В– 180 кг, вида С– 120 кг,

• чистая прибыль от продажи одной упаковки краски типа 1 и 2 составляет соответственно 80 и 65 рублей,

• в таблице 1.4 указан также расход краски каждого типа на одну упаковку.

Таблица 1.4 - Данные к задаче 1.8

Вид реагентов	Тип краски и расход реагентов (кг/ упаковку)		Ограничения ресурсов, кг
	1	2
А	1	1	100
В	0,5	2	180
С	1,5	0,75	120
Время работы оборудования, час/упаковку	0,12	0,4	30 часов
Чистая прибыль, руб./упаковку	80	65

Задача 1.9. В механическом цехе малого производственного предприятия изготавливаются детали шести наименований. Обработка заготовок проводится на пяти станках, имеющих в планируемый период времени известный фонд времени безотказной работы Тi (отражает техническое состояние станка) и стоимость единицы рабочего времени Qi (зависит от сложности детали, косвенно включает зарплату обслуживающего персонала, его квалификацию). В таблице 1.5 кроме этого указано затрачиваемое на обработку деталей время. Критерий эффективности предприятия – прибыль от реализации продукции. Необходимо определить план выпуска деталей, обеспечивающий максимальную прибыль.

Таблица 1.5 – Расчёт плана выпуска деталей на предприятии

1.Станки		Время обработки детали на станке, мин						Стоимость Qi, руб./мин	Фонд Ti, час
		j=1	2	3	4	5	6
		Палец	Вал	Ушко	Ось	Диск	Шкив
i=1	Токарный	5	15	12	15	12	5	0,333	11529
2	Сверлильный	0	5	12	8	12	4	0,233	11340
3	Расточный	0	0	5	0	14	8	0,283	11450
4	Шлифовальный	10	12	10	20	20	12	0,383	11033
5	Фрезерный	0	7	0	25	5	9	0,25	11203
2. Затраты на одну деталь, Sj								Sj =åQi·t
3. Отпускная цена (Cj), руб.		7,85	16,4	16,3	24,6	25,8	15,9
4. Прибыль на одну деталь (Pj ), руб.								Pj= Cj - Sj
5. Программа выпуска (Xj), штук		X1	X2	X3	X4	X5	X6
6. Прибыль по деталям, руб.								(4) · (5)
7. Прибыль общая, руб.

Варианты заданий для анализа системы управления предприятием при изменении внутренних и внешних параметров:

1. Изменилась технология обработки заготовок по отдельным деталям на различных станках (на 10% увеличилось или уменьшилось время обработки детали).

2. Исключена из номенклатуры одна из деталей.

3. Уменьшение на 10% фонда времени одного (двух, всех) типов станков.

4. Увеличение на 20% спроса по одной (двум, всем) деталям.

5. Учесть влияние стоимости заготовок и возможность анализа при различных поставщиках.

Задача 1.10. Фирма, заинтересованная в расширении сбыта продукции, предполагает это сделать посредством систематической рекламы. Финансовые возможности позволяют выделить на эти цели в течение года некоторую сумму Q=40000 рублей. Требуется распределить по кварталам эту сумму на части x_i (i=1, 2, 3, 4) так, чтобы итоговая прибыль была максимальной (исходные данные в таблице 1.6 выделены полужирным шрифтом).

Решение .

1. Построение модели: ограниченность финансов определяет неравенство x₁+x₂+x₃+x₄  Q .

2. C лужба маркетинга фирмы установила, что объем сбыта продукции подвержен сезонным колебаниям и связан с затратами на рекламу формулой V_i =35 K_i (x_i +3000) , где K_i – сезонный фактор.

3. По известным цене C продукции и её себестоимости S можно определить доход D и прибыль P: D=åD_i = åCV_i , P=åP_i =å[(C- S)V_i - x_i].

Задание для анализа: как изменится прибыль от реализации продукции, если на рекламу выделить средств на (10 20)% больше или меньше .

Таблица 1.6 – Анализ затрат на рекламу

Квартал	1	2	3	4	Всего, рубли
Сезонный фактор Ki	0.9	1,1	0,8	1,2
Объем сбыта Vi	2,8	5,1	2,5	5,7	V= 16,1
Доход от реализации Di , руб					Di=С Vi
Себестоимость продукции Si , руб					Si=S Vi
Затраты на рекламу xi , руб	x1	x2	x3	x4	Q= 40000
Прибыль от реализации продукции Pi , руб					P=
Прибыль в % от дохода
Цена продукции C, руб Себестоимость продукции S, руб	40 25

Задача 1.11. Для решения проблем крупного предприятия (например, Ростсельмаш) принято решение создать экспертную группу и подготовить обоснованное решение.

Проблема. Функционирование на грани банкротства.

Цель анализа. Найти пути оптимизации дальнейшего функционирования предприятия, повышения эффективности производства.

Пути решения проблемы:

1. Повысить удельный вес производства средних и небольших сельскохозяйственных машин для использования в фермерских хозяйствах и на ограниченных площадях, в то же время сокращая производство крупных сельскохозяйственных машин.

2. Введение системы покупки сельскохозяйственных машин в кредит на взаимовыгодных условиях (для покупателей и завода - производителя).

3. Создание цехов, работающих параллельно с основным производством и выпускающие, например, бытовые приборы, требующие высоких технологий, для увеличения совокупной прибыли предприятия за счет их продажи.

4. Увеличение затрат, на НИОКР с целью получения государственных субсидий и государственных заказов, повышение конкурентноспособности продукции.

5. Участие в различных выставках сельскохозяйственных машин (включая и международные) с целью демонстрации своей продукции и выхода на новые рынки. Расширение связей с реализаторами.

Решение. Эксперты оценили альтернативные пути путём их ранжирования (таблица 1.7). Степень согласия группы экспертов определяется по величине коэффициента конкордации [1]:

q= 12 S/[э²(k³-k) -12эТ]= 12·150/ [5² ·(5³-5) - (12·5·0)]= 0,6 .

Таблица 1.7 – Пути решения проблем Ростсельмаша

Пути	Эксперты					Итого
	Э1	Э2	Э3	Э4	Э5
П1	1	1	1	1	1	5
П2	2	3	4	3	3	15
П3	5	2	2	2	4	15
П4	4	4	3	4	5	20
П5	3	5	5	5	2	20
Всего	15	15	15	15	15	75

А) оценка согласованности экспертов проводится по формуле Спирмена (э1,э2)=1– 6 d²/(k³-k) :

(э1,э2)=1– 6(0²+1²+3²+0²+2²)/(5³-5) =1- 84/120 = 1- 0,7 = 0,3

(э1,э3)=1– 6(0+4+9+1+4)/120 = 0,1

(э1,э4)=1– 6(0+1+9+0+4)/120 = 0,3

(э1,э5)=1– 6(0+1+1+1+1)/120 = 0,8

(э2,э3)=1– 6(0+1+0+1+0)/120 = 0,9

(э2,э4)=1– 6(0+0+0+0+0)/120 = 1,0 и т.д.

Матрица согласованности мнений экспертов приведена в таблице 1.8.

Таблица 1.8 - Матрица согласованности мнений экспертов

	Эксперты
Эксперты	Э1	Э2	Э3	Э4	Э5
Э1	1	0,3	0,1	0,3	0,8
Э2	0,3	1	0,9	1	0,3
Э3	0,1	0,9	1	0,9	0,1
Э4	0,3	1	0,9	1	0,3
Э5	0,8	0,3	0,1	0,3	1

Б) графы согласованности при критерии важности проблемы =0,7 показывают изолированность экспертов Э1 и Э5, а при =0,3 фиксируют некоторую изолированность эксперта Э3 от экспертов Э1 и Э5 (графы строятся по таблице 1.9).

Таблица 1.9 - Матрица согласованности при разных критериях

Эксперты	к=1 при  0,7 = 						к=1 при  0,3= 
	Э1	Э2	Э3	Э4	Э5		Э1	Э2	Э3	Э4	Э5
Э1	1	0	0	0	1		1	1	0	1	1
Э2	0	1	1	1	0		1	1	1	1	1
Э3	0	1	1	1	0		0	1	1	1	0
Э4	0	1	1	1	0		1	1	1	1	1
Э5	1	0	0	0	1		1	1	0	1	1

В) для оценки рассогласования экспертов формируются матрицы предпочтения (рассогласования) по каждому эксперту (таблица 1.10). Для анализируемого эксперта элемент строки а=1, если соответствующий строке проект имеет лучший ранг по сравнению с рангами проектов столбцов; в противном случае а=-1. При равенстве рангов а=0.

Таблица 1.10 - Матрицы предпочтения мнений экспертов

Пути								Пути
Э1		П1	П2	П3	П4	П5	Э2			П1	П2	П3	П4	П5
	П1	0	1	1	1	1			П1	0	1	1	1	1
	П2	-1	0	1	1	1			П2	-1	0	-1	1	1
	П3	-1	-1	0	-1	-1			П3	-1	1	0	1	-1
	П4	-1	-1	1	0	-1			П4	-1	-1	-1	0	-1
	П5	-1	-1	1	1	0			П5	-1	-1	-1	-1	0

Продолжение таблицы 1.10

Э3						Э4					Э5
	П1	П2	П3	П4	П5	П1	П2	П3	П4	П5	П1	П2	П3	П4	П5
П1	0	1	1	1	1	0	1	1	1	1	0	1	1	1	1
П2	-1	0	-1	-1	1	-1	0	-1	1	1	-1	0	1	1	1
П3	-1	1	0	1	1	-1	1	0	1	1	-1	-1	0	-1	-1
П4	-1	1	-1	0	1	-1	-1	-1	0	1	-1	-1	1	0	-1
П5	-1	-1	1	1	0	-1	-1	-1	-1	0	-1	-1	1	1	0

Сравнивая мнения экспертов по матрицам предпочтения, определяем матрицу рассогласования мнений (таблица 1.11). Элементы матрицы определяются по формуле r(Е,М)=1/2 e_ij–m_ij для каждой пары экспертов.

r(Э1,Э2) = ½ (2+2+2+2+2+2+2+2)=8,

r(Э1,Э3) = ½ (2+2+2+2+2+2+2+2+2)=10,

r(Э1,Э4) = ½ (2+2+2+2+2+2+2+2)=8,

. . . . . . . . . . . . . . . .

r(Э2,Э4) =0,

r(Э3,Э4) = ½ (2+2)=4 и т.д.

Таблица 1.11 - Матрицы рассогласования мнений экспертов

Эксперты						Сумма рассогласований	Доля, %
	Э1	Э2	Э3	Э4	Э5
Э1	0	8	10	8	4	30	25
Э2	8	0	2	0	8	18	15
Э3	10	2	0	2	10	24	20
Э4	8	0	2	0	8	18	15
Э5	4	8	10	8	0	30	25
Всего	30	18	24	18	30	120	100

По таблице 1.11 видно, что всего рассогласований в оценке путей было 120 при доле каждого эксперта от 15 до 25 процентов. Принимая коэффициент согласованности к=1 при числе рассогласований  8, для наглядности можно построить матрицу и граф согласованности мнений. Вывод: эксперты действовали достаточно согласовано, следует принять во внимание мнение каждого эксперта.

Окончательное решение. По мнению привлечённых к решению проблемы экспертов наиболее предпочтительно прежде всего применить первый путь. На втором этапе при наличии средств целесообразно использовать второй и третий пути. Менее эффективными являются четвёртый и пятый пути.

Задача 1.12. Необходимо выбрать наилучший вариант улучшения экономических показателей фирмы, производящей косметику. Предложены три проекта и создана экспертная группа из четырёх специалистов:

Э1 - главный инженер, Э2 - коммерческий директор,

Э3 - директор по экономическим вопросам, Э4 - менеджер по труду.

Результаты экспертизы сведены в таблицу 1.12.

Таблица 1.12 - Оценки проектов

Проекты	Эксперты				Сумма баллов Ri
	Э1	Э2	Э3	Э4
П1	1	2	1	2	6	П1- открыть фирменный магазин
П2	3	3	2	1	9	П2 - усилить рекламу продукции
П3	2	1	3	3	9	П3 - усилить подготовку персонала
Всего	6	6	6	6	24

Необходимо рассчитать степень согласия группы экспертов и оценки согласованности пар экспертов.

Задача 1.13. Определить степень беспорядка в оценках экспертов по таблице из задачи 1.12.

Решение. Степень беспорядка в оценках экспертов рассчитывается по формуле =1-4/к(к-1). Для Э1 и Э2 имеем одну инверсию в оценке проектов П1 и П3, поэтому =1, к=3; следовательно,

(Э1,Э2)= 1- 4/к(к-1)= =1- 41/ 3(3-1)= 0,33.

Аналогично степень беспорядка рассчитывается для других пар экспертов (таблицу 1.13 заполнить самостоятельно).

Таблица 1.13 - Степень беспорядка в оценках экспертов

Эксперты	Э1	Э2	Э3
Э1	0	0,33
Э2		0
Э2			0

Задача 1.14. Рассчитать предельные значения ранговоё кореляции пар экспертов и степени беспорядка в оценках экспертов при различных величинах количества проектов, критериев и числе экспертов.

Задача 1.15. Решить задачи 1.6, 1.7, 1.8, 1.9, 1.10, 1.11 с использованием инструментальных средств (например, Excel) и моделировании системы при изменении исходных данных.

Задача 1.16. Предприятие планирует провести перестройку своего производства. На конкурсной основе были разработаны три проекта, каждый из которых приемлем в отдельности, однако общий объём расходов превышает финансовые возможности предприятия. Для анализа экономической эффективности проектов были выделены пять критериев:

К1 – чистая текущая стоимость (тыс. рублей),

К2 – рентабельность инвестиций,

К3 – внутренняя норма прибыли (проценты),

К4 – период окупаемости инвестиций (лет),

К5 – бухгалтерская рентабельность инвестиций (проценты).

На основании планируемых годовых доходов на пять лет по каждому проекту рассчитаны значения указанных критериев (таблица 1.14). Необходимо провести сравнительный анализ проектов.

Таблица 1.14 – Значения критериев Таблица 1.15 – Ранжирование проектов

Проекты	Критерии						Ранг	Критерии
	К1	К2	К3	К4	К5			К1	К2	К3	К4	К5
А	6,0	1,2	15,0	3,5	7,8		3	С	С	С
В	18,0	1,2	16,0	4,5	5,5		2	В	А,В	В
С	21,0	1,5	17,0	4,0	10,0		1	А		А

Таблица 1.16 – Таблицы предпочтений

А	В	С		В	А	С		С	А	В
К1	-	-		К1	+	-		К1
К2	0	-		К2	0	-		К2
К3	-	-		К3	+	-		К3
К4	+	+		К4	-	-		К4
К5	+	-		К5	-	-		К5

Решение по методу Парето. Согласно правилу Парето [9] лучшим является проект, для которого нет другого проекта по всем показателям не хуже его, а хотя бы по одному показателю лучше. По таблице 1.14 составим таблицу ранжирования проектов (таблица 1.15), а по ней - таблицу предпочтения (таблица 1.16), где сравниваются все проекты попарно; например, для пары (X, Y ) знак “+” означает, что Кi (X) > Кi (Y),

знак “” означает, что Кi (X) < Кi (Y),

знак “0” означает, что Кi (X) = Кi (Y).

По таблице 1.16 наличие в паре (В,С) столбца со знаками “-” означает, что проект В по всем критериям хуже проекта С. Поэтому проект В на первом этапе исключается из дальнейшего рассмотрения.

Для оставшихся проектов А и С проведём аналогичные процедуры (таблица 1.17).

Таблица 1.17 – Результаты второго этапа по правилу Парето

	Ранги			Проекты			Проекты
	2	1		А	С		С
К1	С	А		К1			К1
К2	С	А		К2			К2
К3	С	А		К3			К3
К4	А	С		К4	+		К4
К5	С	А		К5			К5

В этом случае правило Парето не позволяет сделать вывод о явном превосходстве одного из проектов, т.к. имеется ситуация К4 (С) < К4 (А) при превосходстве проекта С по всем остальным критериям.

Вывод. По правилу Парето худшим признаётся проекту В.

Решение по методу Борда также предполагает ранжирование по каждому критерию в порядке убывания с присвоением им соответствующих значений ранга, а затем подсчитывается суммарный ранг по каждому проекту. Победителем процедуры выбора становится проект с максимальным значением суммарного ранга.

Из таблицы 1.14 или 1.15 получаем таблицу рангов проектов (таблица 1.18), из которой видно, что наилучшим по правилу Борда на первом этапе будет проект С (сумма баллов 14).

Таблица 1.18 – Ранги (этап 1) Таблица 1.19 – Ранги (этап 2)

Проекты	Критерии					Сумма рангов		Проекты	Критерии
	К1	К2	К3	К4	К5				К1	К2	К3	К4	К5
А	1	2	1	3	2	9		А	1	2	1	2	2
В	2	2	2	1	1	8		В	2	2	2	1	1
С	3	3	3	2	3	14

На втором этапе после исключения проекта С по таблице рангов (таблица 1.19) лучший проект выбрать нельзя (сумма баллов у обоих равна 8). В таких случаях при необходимости используют дополнительные ограничения, например, на общую сумму финансирования проекта, или учёт относительного веса каждого критерия для данной фирмы.

Решение с использованием весовых коэффициентов. Для определения весовых коэффициентов критериев создадим группу экспертов в составе четырёх человек. Результаты их работы приведены курсивом в таблице 1.20; затем по указанным в таблице формулам проведена обработка порядковых оценок и получены значения весовых коэффициентов w_i .

Таблица 1.20 – Оценка важности критериев

Эксперты (j)	Критерии (i)
	K1 K2 K3 K4 K5
Э1 Э2 Э3 Э4	3 2 4 1 5 3 2 4 1 5 4 2 3 1 5 4 2 3 1 5	t= p=
Ri = åri Vi = R min/Ri	14 8 14 4 ? 0,29 0,5 0,29 1,0 ?	Rmin = 4 åVi = 2,28
wi = Vi / åVi	0,13 0,22 0,13 0,44 ?	åwi = 1

С учётом таблицы 1.18 и полученных весовых коэффициентов получим потенциальную эффективность проектов:

Е (А)= 1 0,13 + 20,22 +10,13 + 30,44 +20,08 =2,18;

Е (В)= 2 0,13 + 20,22 +20,13 + 10,44 +10,08 = ;

Е (С)= 3 0,13 + 30,22 +30,13 + 20,44 +30,08 =2,56.

Вывод. При данных весовых коэффициентах критериев лучшую оценку имеет проект С, затем проект А (85 % от оценки проекта С), низкая оценка у проекта В (58 %).

Задача 1.17. Необходимо оценить три проекта по четырём критериям группой из пяти экспертов. Перечень критериев: К1 – минимум времени на внедрение, К2 – максимальная простота для пользователя, К3 – минимальные затраты на разработку, К4 – максимальная экономическая эффективность. В таблице 1.21 приведены результаты качественной оценки проектов, которая преобразована в количественную оценку по следующей шкале: 5 – проект полностью удовлетворяет критерию,

4 - проект удовлетворяет критерию в значительной степени,

3 – проект соответствует среднему уровню требований критерия,

2 – проект соответствует уровню ниже среднего,

1 – проект очень мало удовлетворяет критерию,

0 - проект не удовлетворяет критерию.

Эксперты оценили также относительную значимость каждого критерия путём их ранжирования (таблица 1.21).

Таблица 1.21 - Оценка альтернативных проектов по критериям

Критерии	Проекты				Эксперты
	П1	П2	П3		Э1	Э2	Э3	Э4	Э5
К1	4	5	4		2	3	1	2	1
К2	2	2	4		3	2	3	4	3
К3	3	3	5		4	4	4	3	4
К4	3	3	2		1	1	2	1	2

Возможные варианты принятия решения:

а) выбор наилучшего проекта по максимуму суммарной оценки,

б) выбор наилучшего проекта с учётом весовых коэффициентов критериев. Для этого после расчёта весовых коэффициентов необходимо рассчитать потенциальную эффективность проектов, например, для П1:

Е (П1)= 4 w₁+ 2 w₂ + 3 w₃+ 3 w₄ ,

в) использовать методику приведения многокритериальных оценок к единой системе [1].

Необходимо оценить также степень согласия экспертов при оценке значимости критериев (коэффициент конкордации).

Задача 1.18. Провести сравнительный анализ квалификации групп экспертов по результатам их работы при решении задач 1.11, 1.12, задачи 1.15 и 1.16 путём определения коэффициента конкордации, выборочной оценки согласованности экспертов и степени беспорядка в их работе.

Задача 1.19. Определить предельные значения коллективных и индивидуальных оценок экспертов, принимавших участие в работе экспертных групп при решении предыдущих задач 1.

Задача 1.20. Эксперты двумя составами оценили ранги двух групп критериев К1К4 и К5К9 (таблица 1.22). Каковы весовые коэффициенты этих критериев по их оценкам? Как можно оценить согласованность мнений этих экспертов?

Таблица 1.22 – Оценки критериев

	Критерии					Критерии
	К1	К2	К3	К4		К5	К6	К7	К8	К9
Э1	1	2	3	4		2	3	4	1	5
Э2	1	2	4	3		3	1	5	2	4
Э3	1	2	3	4		1	4	5	2	3
Э4	2	1	3	4

Задача 1.21. Рассчитать весовые коэффициенты и оценить экспертов, если после экспертизы установлено:

А) полное единодушие (таблица 1.23-А),

Б) явно выраженное противоречие (таблица 1.23-Б),

В) явно выраженный приоритет одного из критериев (таблица 1.23-В),

Г) выставление экспертами количественных оценок вместо ранговых (таблица 1.24).

Таблица 1.23 – Варианты ранжирования

А	Критерии					Б	Критерии					В	Критерии
	К1	К2	К3	К4			К1	К2	К3	К4			К1	К2	К3	К4
Э1	1	2	3	4		Э1	1	2	3	4		Э1	1	2	4	3
Э2	1	2	3	4		Э2	4	1	2	3		Э2	1	2	3	4
Э3	1	2	3	4		Э3	3	4	1	2		Э3	1	3	2	4
Э4	1	2	3	4		Э4	2	3	4	1		Э4	1	3	4	2
Э5	1	2	3	4								Э5	1	4	3	2

Таблица 1.24 – Варианты оценки критериев

А	Критерии					Б	Критерии					В	Критерии
	К1	К2	К3	К4			К1	К2	К3	К4			К1	К2	К3	К4
Э1	1	3	4	6		Э1	1	3	4	6		Э1	1	3	4	6
Э2	1	3	4	6		Э2	6	1	3	4		Э2	1	4	3	6
Э3	1	3	4	6		Э3	4	6	1	3		Э3	1	4	6	3
Э4	1	3	4	6		Э4	3	4	6	1		Э4	1	3	6	4
Э5	1	3	4	6								Э5	1	6	4	3

Задача 1.22. Для фирмы, где Вы работали менеджером, проведите анализ взаимодействия внешней и внутренней среды на основании методики SWOT.

Задача 1.23. Разработать сценарий качественного улучшения подготовки менеджеров в системе высшего образования России. Предусмотреть три альтернативные программы, рассчитанные на пять лет.

Задача 1.24. Провести выбор наилучшего устройства отдельно для профессионального и бытового использования, используя методику «морфологического ящика». В качестве устройств можно выбрать оргтехнику (диктофон, ПЭВМ, монитор, сканер, принтер и т.п.), видеотехнику (проигрыватель, устройство для перезаписи, кинокамера и т.п.), а также холодильник, пылесос, газовую плиту, электронагревательные приборы и другие распространённые устройства. Оценку провести по 5-8 параметрам с учётом их значимости; выбор проводится среди 4-7 устройств одного вида.

Задача 1.25. Решить задачи 1.16, 1.18, 1.23, 1.24, 1.26 с использованием инструментальных средств (например, Excel) и моделировании системы при изменении исходных данных.

Задача 1.26. Решить задачу 1.16 методом нормализации разнонаправленных критериев. Исходные данные задачи 1.16 повторены в таблице 1.26 (из таблиц 1.14 и 1.20).

Метод нормализации разнонаправленных критериев предполагает пересчёт значений максимизируемых критериев К1, К2, К3 и К5 по формуле H_ij = (y_ij - y_i ^min) / (y_i ^max - y_i ^min) - подробно смотри в работе [1] и

минимизируемого критерия К4 по формуле H_ij=(y_i ^max - y_ij) / (y_i ^max- y_i ^min).

Результаты пересчёта приведены в таблице 1.27, где также показаны значения показателя относительного соответствия W(j) = w_iH_ij (свободные клетки заполнить самостоятельно).

Таблица 1.26 – Пересчёт разнонаправленных критериев

	Критерии						Hij	Критерии
	К1	К2	К3	К4	К5			К1	К2	К3	К4	К5
А	6,0	1,2	15,0	3,5	7,8		А	0	0	0
В	18,0	1,2	16,0	4,5	5,5		В	0,8	0
С	21,0	1,5	17,0	4,0	10,0		С	1	1
Y(max)	21,0	1,5					Е (А) = 0,130 + 0,220 + 0,130+…….=
Y(min)	6,0	1,2					Е (В) = 0,130,8+0,220 +…………=
y	15	0,3					Е (С) = 0,131 + 0,221 +…………….=
wi	0,13	0,22	0,13	0,44

Вывод. Максимальное значение показатель относительного соответствия имеет проект …., далее следуют проекты …. и …. .

Задача 1.27. Провести выбор среди трёх проектов системы информации, оцененных экспертами по четырём критериям, имеющим разную значимость (таблица 1.27):

К1 – минимум времени на внедрение, К2 – максимум простая для пользователя,

К3 – минимум затрат на разработку, К4 – максимум экономической эффективности.

Таблица 1.27 – Оценка экспертов

	Проекты			wi	Выбор проектов провести для трёх различных вариантов: 1. В таблице указаны действительные (расчётные) значения критериев в условных единицах. 2. В таблице указаны расчётные значения критериев, которые необходимо перевести в ранговые оценки. В таблице указаны результаты качественной оценки проектов в условных единицах соответствия цели (по шкале аналогично задаче 1.17).
	П1	П2	П3
К1	4	5	4	0,30
К2	2	2	4	0,18
К3	3	3	5	0,14
К4	3	3	2	0,38
E	?	?	?

Задача 1.28. Предприятие решили внедрить новую систему с автоматизацией расчётов и объединением вычислительных средств в локальную сеть. Анализ условий внедрения альтернативных проектов показал, что они должны удовлетворять следующим критериям:

К1 – минимум затрат (тыс. руб.),

К2 – максимальные возможности использования сложных структур данных (шт.),

К3 – минимум времени ответа и поиска данных (сек.),

К4 – максимум возможностей расширения и изменений в базе данных (блоков),

К5 – минимум эксплуатационных расходов (тыс. руб.).

Из трёх имеющихся проектов систем с использованием различных технических средств необходимо выбрать наиболее эффективную систему. Группа экспертов провела количественную оценку проектов по пяти критериям, среди которых проведено ранжирование (таблица 1.28).

Таблица 1.28 – Оценки экспертов

	Проекты					Ранжирование экспертами критериев
	П1	П2	П3			Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8
К1	4	5	5		К1	1	2	1	2	1	1	2	1
К2	3	2	4		К2	3	1	2	1	2	2	1	2
К3	4	3	2		К3	2	2	3	3	3	4	3	3
К4	2	4	3		К4	2	3	4	4	5	3	4	4
К5	3	2	1		К5	4	4	5	5	4	5	5	5

Задача 1.29. Результаты стратегий S1S4 работы фирмы в разных условиях V1V4 среды (с учётом вероятности их проявления) представлены в таблице 1.29. Какая стратегия является наилучшей и почему?

Таблица 1.29 - Результаты стратегий

Стратегии	Среда и её вероятность
	V1 (p1=0,1)	V2 (p2=0,2)	V3 (p3=0,4)	V4 (p4=0,3)
S1	10	8	6	5
S2	12	10	8	8
S3	10	10	10	6
S4	18	14	6	2

Задача 1.30. Провести количественный анализ организационных структур системы управления, представленных на рисунке 1.1. Необходимо дать общую характеристику оргструктуры, определить её параметры. Рассчитать характеристики структуры.

Решение (для структуры на рисунке 1.1а).

1. Структура иерархическая с параметрами р=4 и q=3, двухуровневая (показатель Ур=2).

2. По матрице смежности (таблица 1) определяем величины i, Nск (смотри таблицу 1.1), N_рс=3, _ср = Σ_i / p =(1+3+1+1) /4 =1,5 и коэффициент структурной избыточности по формуле

Rстр =[q/(p-1)] –1=[3/(4 –1)]-1= 0.

Эти показатели отражают простоту и низкую надёжность структуры.

3. Коэффициенты неравномерности связей:

Е=  Σ(_i - _ср)² =  (1-1,5)²+(3-1,5)²+(1-1,5)²+(11,5)² =  3 =1,73.

Для структуры типа “звезда“ имеем ’ср=2(p-1)/p=23/4=1,5 , поэтому

Е_max= (p-1-’_ср)² +(p-1)(1-’_ср)² = (3-1,5)² +3(1-1,5)² = 3 =1,73 и

Е_отн = Е/Е_max =1,73/1,73= 1.

Вывод: структура потенциально ненадёжна, отказ элементов существенно влияет на управление.

4. По дистанционной матрице (таблица 1.30) определяем:

• диаметр структуры d=max d_ij =2 для элементов 1, 3 и 4;

- показатели структурной компактности Q =  d _ij =18,

Qmin =p(p-1) =4(4-1)=12,

Qотн =(Q/Qmin) –1 =(18/12) – 1=0,5

или Qотн =Qmin / Q= 12/18 =0,66.

Вывод: инерционность информационных процессов средняя.

Таблица 1.30 – Матрицы смежности и дистанционная

Матрица смежности											Матрица дистанционная
Sij		Вершины, j				i	Nск	Npc				Dij		Вершины, j				 dij	Max dij	Zi
		1	2	3	4									1	2	3	4
i=	1	0	1	0	0	1	1	-				i =	1	0	1	2	2	5	2	1,8
	2	1	0	1	1	3	2	1					2	1	0	1	1	3	1	3,0
	3	0	1	0	0	1	0	1					3	2	1	0	2	5	2	1,8
	4	0	1	0	0	1	0	1					4	2	1	2	0	5	2	1,8
					=6			=3		Q =   dij=18									 =1

5. В таблице 1.30 приведены показатели центральности для основных руководителей (в узлах верхних уровней), рассчитанные по формуле Zi = Q/ 2d_ij.

6. Индекс центральности системы определяется по формуле  = [(р-1) (2 Z_i^max – р)]/ [Z_i^max (p-2)] = [(4-1)(23 – 4)] / [3(4-2)]=1.

В ывод: центральным является второй элемент, через него проходят все связи (100%).

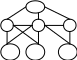
А) 1 б) 1 в) 1 г)

2 2 2 3 4 p=7

q=11

3 4 3

5 6 7

4

Рисунок 1.1 – Организационные структуры СУ

Задача 1.31. Для фирмы, на которой Вы проходили производственную практику, провести декомпозицию системы управления, выделив подсистемы, процессы, процедуры управления; для одной подсистемы – блоки задач и операций, выполняемых людьми и компьютерными средствами. Дать комментарий к системе управления.

Пример решения. Фирма … (ДГАС) предназначена для ……… . Организационная структура системы управления фирмой имеет чётко выраженную древовидную (иерархическую) систему управления (рисунок 1.2) и включает шесть подсистем. Выделить в этой системе административную систему управления по персональной подчинённости и выполнить оценку её структуры:

а) иерархическая двухуровневая, плоская, …

б) параметры структуры - число элементов n =

- число связей m =

в) характеристики структуры - структурная избыточность R = ,

- число решающих связей, - оценка сфер контроля,

- коэффициент неравномерности связей E= и Еотн = ,

- диаметр системы d= ,

- структурная компактность Q = и Qотн = ,

- индекс центральности = , Zi= .

Дирекция (директор, зам. директора, секретариат, канцелярия)

П

О Д

С

И С Т

Е М Ы

Учебная часть

Бухгалтерия

Отдел кадров

Медчасть

Библиотека

Автомобильное хозяйство

Обучение учащихся

Учет и распределение заработной платы

Учет ….

Учет и подготовка работников

Профилактика и лечение учащихся и сотрудников

Обеспечение учебной литературой, информационное обеспечение

Обеспечение задач, связанных с транспортировкой

Исполнители

Рисунок 1.2 - Схема системы управления ДГАС

Отдел кадров работает по двум направлениям и выполняет функции:

1. Учёт работников ДГАС.

1.1…….

1.2……и т.д.

2. Подготовки специалистов для фирмы.

2.1………и т.д. перечисляются процессы и процедуры.

С использованием оргтехники выполняются следующие трудоёмкие блоки задач и операции (перечислить); при этом используются технические и программные средства (перечислить). В системе управления выделяются положительные стороны (перечислить); среди недостатков следует отметить (перечислить). Дополнительно предлагается (перечислить).

Вывод. Система управления ДГАС обеспечивает эффективное управление фирмой.

Задача 1.32. В трех городах Ростовской области (А1 – Каменск-Шахтинский, А2 – Новочеркасск, А3 – Ростов-на-Дону) химические комбинаты производят определенную продукцию. На складах этих городов хранится однородный груз в количестве 200, 205 и 225 тонн. Этот груз требуется перевезти в пять пунктов назначения (В1 – Батайск, В2 – Зерноград, В3 – Миллерово, В4 – Пролетарск, В5 – Шахты), потребности которых составляют 190, 130, 80, 100 и 130 тонн. Расстояние S_ij между пунктами отправления и пунктами назначения приведены в таблице 1.31.

Таблица 1.31 – Исходные данные (в тоннах и километрах)

	B1 = 190	B2 = 130	B3 = 80	B4 = 100	B5 = 130
A1 = 200	160	220	75	350	75
A2= 205	50	120	180	250	35
A3 = 225	10	75	220	200	75

Дополнительно для анализа предлагаются два случая:

а) суммарные запасы превышают суммарные потребности;

б) суммарные потребности превышают суммарные запасы.

Задача 1.33. Рассчитать оптимальный план перевозок грузов, сосредоточенных на двух складах в количестве 6 и 11 единиц, если четыре потребителя требуют соответственно 2, 3, 5 и 7 единиц груза. Стоимость перевозки единицы груза составляет из первого склада 7, 3, 2 и 3 у.е., а из второго склада соответственно 3, 2, 4 и 6 у.е.

Задача 1.34. Рассчитать оптимальный план перевозок грузов, сосредоточенных на трёх складах в количестве 10, 15 и 20 единиц, если четыре потребителя требуют соответственно 15, 15, 10 и 5 единиц груза. Стоимость перевозки единицы груза составляет из первого склада 2, 3, 4 и 4 у.е., из второго склада - 3, 4, 2 и 3 у.е., а из третьего – соответственно 1, 3, 2 и 4 у.е.

Задача 1.35. Составить сбалансированную таблицу перевозок из четырёх складов, имеющих в сумме 60 единиц груза, если известны заявки пяти потребителей и время перевозки от каждого склада каждому потребителю.

Задача 1.36. Фирма по прокату автомобилей собирает заявки на аренду во всех городах юга России для проезда по курортам Черноморского побережья. Турист имеет возможность получить автомобиль в любом удобном для него населённом пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своём родном городе (шофер фирмы забирает автомобиль и перегоняет его для передачи новому туристу). Известны расстояния между городами, где сейчас оставлены автомобили фирмы (Таганрог– 4 шт., Ростов–на-Дону - 3 шт., Краснодар – 6 шт., Туапсе – 1 шт.) и где имеются заказы туристов (Сочи – 5, Ейск – 3, Анапа - 6). План работы фирмы должен быть ориентирован на минимизацию расстояния, которые пройдут все перегоняемые автомобили. При этом возможны сообщения о дополнительных автомобилях (например, один в Ставрополе) и клиентах в разных городах (например, один в Геленджике).