Оценка ошибок измерений и запись результатов.

1. Вычисление случайной ошибки прямых измерений.

Для выявления случайной ошибки измерения необходимо повторить насколько раз.

• Получим N значений величины х: х₁, х₂, х₃ ….. х_N.

• Вычислим среднее значение

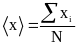
• Вычислим абсолютную ошибку каждого измерения

• Вычислим абсолютную случайную ошибку серии измерений как среднее арифметическое

Тогда результат измерений представим в виде:

При вычислениях часто приходится округлять результаты вычислений. Ошибка, возникающая при округлении результатов вычислений, должна быть согласована с ошибкой самих измерений. При этом нужно придерживаться следующего правила.

Ошибка, получающаяся в результате вычислений, должна быть того же порядка что и ошибка измерений.

Например, при вычислении получены следующие результаты:

Так как абсолютная ошибка показывает, в каком знаке измеренной величины появится ошибка, то значение абсолютной ошибки нужно округлить до первой значащей цифры, следовательно

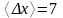. Видно, что ошибка появляется в единицах, поэтому измеренную величину нужно округлить до единиц и записать

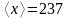. Окончательный результат представим в виде (с указанием размерности величины х):

.

Более подробно вопрос об ошибке вычислений изложен в Приложении.

2. Вычисление случайной ошибки косвенных измерений.

Определяемая косвенным измерением величина может быть вычислена по формуле . Величины и получены прямыми измерениями. Таким образом, известно

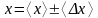и ,

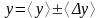надо найти 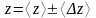. Наиболее достоверное или истинное значение измеряемой величины равно

Расчет абсолютных ошибок косвенных измерений производится с использованием правил вычисления бесконечно малых величин. Бесконечно малое изменение , вызванное бесконечно малыми изменениями переменным и , равно

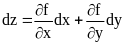
Частные производные и могут быть как положительными, так и отрицательными. В отношении ошибки наиболее неблагоприятны случаи, когда все члены суммы имеют одинаковый знак. Поэтому возьмем модули частных производных. Поскольку приращения всех величин являются случайными отклонениями от истинных значений, т.е. ошибками измерений, то с точностью до знака можно записать

, ,

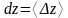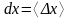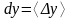
Тогда для оценки случайной абсолютной ошибки косвенных измерений получим

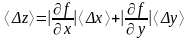
Относительная ошибка измерений

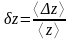
Ниже в таблице приведены формулы для расчета ошибки косвенных измерений, полученных по правилам, сформулированным выше, для некоторых часто встречающихся функций.

Таблица I

Расчет ошибок косвенных измерений.

(Эта таблица не используется для выполнения лабораторной работы)

N п./п.	Зависимость	Ошибка
		Абсолютная	Относительная
1.
2.
3.
4.
5.
6.
7.

Доверительный интервал и доверительная вероятность.

Измеренные физические величины и случайные ошибки имеют вероятностный характер. Измеренное значение и случайная ошибка образуются в результате совокупности огромного количества «мелких», не поддающихся учету факторов, каждый из которых вносит незначительный вклад в случайную ошибку. Часть этих «мелких» ошибок положительная, часть – отрицательная. Измеренное значение и случайная ошибка получается в результате сложения всех таких ошибок, и могут иметь разные значения, каждому из которых соответствует разная вероятность.

За наиболее вероятное значение, которое считают истинным значением измеряемой величины, принимают среднее арифметическое значение всего ряда измеренных значений .

Результат некоторого опыта отличается от наиболее вероятного значения на величину

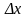. Пусть вероятность того, что результат измерения отличается от истинного на величину, не большую, чем

. Величина – носит название доверительной вероятности, а интервал значений от ( –

) до ( +

)называется доверительным интервалом.

Проведя N равноточных опытов, получают значений физической величины. Рассчитывают наиболее вероятное (среднее) значение . Задают доверительный интервал от –

до +

. Если в этом интервале находятся результаты измерений, то доверительной вероятностью называется

Таким образом, для оценки случайной ошибки необходимо знать два числа: доверительный интервал и доверительную вероятность. Очевидно, чем больше доверительный интервал, тем больше доверительная вероятность. Если доверительный интервал принять равным средней абсолютной ошибке , то доверительная вероятность будет равна . Это значит, что из 100 опытов в интервале от –

до +

окажется 57 результатов. Некоторые значения доверительных интервалов и соответствующих им доверительных вероятностей приведены ниже:

Доверительный интервал
Доверительная вероятность	0,31 (31%)	0,57 (57%)	0,89 (89%)	0,98 (98%)

Таким образом, записанный результат измерений физической величины в виде выражения:

имеет следующий смысл: