Записи результатов измерений. Ошибки вычислений.
«Экономисты используют в своих прогнозах десятые доли процента, чтобы доказать наличие у них чувства юмора»
Удачная шутка.
Результаты
измерения физической величины
записываются
в виде:
|
с
указанием размерности
.
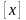Например:
.
В
этом выражении
наиболее вероятное, наилучшее значение
х, а
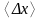случайная абсолютная ошибка проведенной
серии измерений.
Величины и вычисляются как средние арифметические серии равноточных измерений. При вычислениях часто получаются числа, содержащие большое или бесконечное количество значащих (не равных нулю) цифр. Такие числа необходимо округлять. При округлении возникает ошибка, которая является ошибкой вычислений. Округляя такие числа до разных цифр, мы получаем различные ошибки вычислений.
Ошибка, появляющаяся в процессе арифметических вычислений, должна быть согласована с ошибкой измерений.
Вычисления, произведенные с большим числом десятичных знаков, чем это необходимо, требуют лишних затрат времени и, главное, создают ложное впечатление о большой точности измерений. Поэтому, выполняя арифметические вычисления необходимо придерживаться следующего правила:
Ошибка, получающаяся в результате вычислений должна быть того же порядка что и ошибка измерений.
Поясним это правило на примере.
Пример. Исследуя равномерное движение тела, были получены в результате прямых измерений следующие результаты:
-путь,
пройденный тело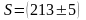м
м
-время
движения
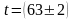с.
Вычисления скорости дали, следующие результаты:
скорость:
абсолютная
ошибка: 
Значение
скорости следует округлить
до
«десятых», поскольку ошибка измерений
(первая значащая цифра в
)
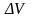появляется в «десятых».
Поэтому окончательный результат следует записать так:
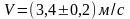
Сформулированное выше правило имеет следующий смысл:
Записывая значение физической величины последней должна указываться цифра того десятичного разряда, который равен разряду ошибки |
Например, величина х=1,27483 в зависимости от ошибки измерения запишется в виде:
;
;
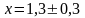Таким образом, последняя из указанных в числе цифр является сомнительной, а остальные цифры достоверные.
Сформулированное
правило следует применять и в тех
случаях, когда последние цифры являются
нулями. Если при измерении получен
результат
,
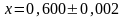то писать нули в конце числа 0,600 необходимо,
поскольку все эти цифры достоверны.
Запись х=0,6 означала бы, что следующие
после 6 цифры этого числа сомнительны,
в то время как измерения показали, что
они равны нулю.
Сформулированное правило относится не только к записи результата измерения, но и к записи ошибки.
При вычислении ошибки следует округлять ее величину до одной (первой) значащей цифры.
|
У этого правила есть исключение:
Если первая цифра ошибки является единицей, то округляют до двух (первых) значащих цифр.
Так,
если вычисленные ошибки равны:
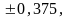
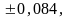то правильно
записать:
,
.
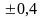
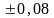