Расчетные формулы.

1. За время одного оборота шкива радиуса r с намотанной на него нитью груз перемещается на расстояние равное длине окружности 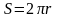. Движение груза массой m является равноускоренным (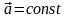 ). Поскольку в момент времени t=0 скорость V₀=0, то закон движения груза имеет вид:

,

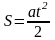отсюда ускорение груза равно

Это ускорение равно тангенциальному ускорению точек обода шкива 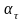, которое может быть выражено через угловое ускорение ε:

Расчетная формула для углового ускорения имеет вид:

(1)

2. Рассмотрим вращательное движение стержня с укрепленными на нем дисками и поступательное движение груза на нити – рис.1.

Уравнение поступательного движения груза в проекции на ось Х имеет вид:

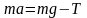
откуда

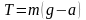или

Момент силы натяжения нити равен:

или

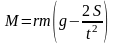
Расчетная формула для момента силы натяжения имеет вид:

(2)

Момент инерции по определению равен:

Поэтому учитывая (1) и (2) получим расчетную формулу для момента инерции:

(3)

Это один из двух способов определения момента инерции. Назовем этот способ «первым». Вычисленный по (3) момент инерции обозначим . Второй способ вычисления изложен ниже, в пункте 4.

3. Для вычисления ошибок используют следующие формулы:

Случайная абсолютная ошибка прямых измерений времени:

(4)

Случайная относительная ошибка прямых измерений времени:

(5)

Случайная абсолютная ошибка косвенных измерений углового ускорения из (1):

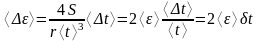(6)

Случайная абсолютная ошибка косвенных измерений момента силы из (2):

(7)

Случайная абсолютная ошибка косвенных измерений момента инерции из (3):

(8)

5. Момент инерции можно вычислить другим способом. Обозначим результат этого способа вычисления .

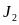Момент инерции системы равен сумме моментов инерций стержня и двух одинаковых дисков :

,

Момент инерции однородного стержня относительно оси, проходящей через его центр масс равен:

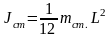
где – масса, а 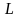- длина стержня.

Момент инерции диска относительно оси вращения, которая совпадает с осью диска, равен:

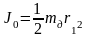
где 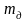- масса, а 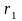– радиус диска.

Поскольку центр инерции диска, укрепленного на стержне, находится на расстоянии R от оси вращения (рис.1), то момент инерции рассчитывают по теореме Штейнера:

Тогда вторая расчетная формула для момента инерции имеет вид:

(9)

Величины, необходимые для вычисления записать в таблицу I.