Расчетные формулы

Энергия первого шара отклоненного от положения равновесия на угол , равна:

где 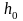– высота подъема первого шара (рис. 3), – масса шара, – ускорение сво­бод­ного падения. Учитывая геометрическое равенство (см. рис. 3)

,

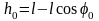получаем расчетную формулу для энергии шара 1 до удара:

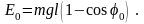(1)

Шар 2 до удара покоится. После удара этот шар поднимается на высоту

,

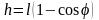где – измеряемый угол отклонения шара 2. Механическая энергия шара 2 после удара сохраняется: кинетическая энергия в положении равновесия переходит в потенциальную энергию, то есть

,

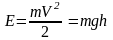где 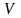– скорость шара 2 после соударения с шаром 1. Отсюда получаются рас­четные формулы для энергии и скорости шара 2 после удара:

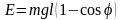, (2)

. (3)

Эту энергию (2) налетающий (правый) шар 1 передал покоящемуся (левому) шару 2 в процессе удара. Доля переданной энергии равна

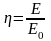, (4)

где (1) – энергия шара 1 до удара, (2) – энергия шара 2 после удара.

При абсолютно упругом ударе механическая энергия сохраняется. Если про­исходит абсолютно упругий центральный удар шаров одинаковой массы, на­летающий шар останавливается, а покоившийся до удара шар получает всю энергию налетающего (т.е. , 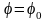), и доля переданной энергии . Однако некоторая часть механической энергии при соударении переходит в другие виды энергии, поэтому угол оказывается меньше и .

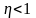Ошибка 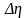косвенных измерений доли зависит от ошибки 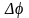пря­мых измерений угла по формуле

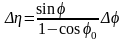. (5)

Угол выражен в радианах.

Среднюю силу удара можно найти по второму закону Ньютона:

,

где 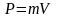– импульс шара 2 после удара, 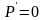– импульс шара 2 до удара, – измеряемое время соударения. Отсюда получается расчетная формула для силы удара

, (6)

где скорость берется из формулы (3).

Ошибка косвенных измерений силы удара определяется ошибками прямых измерений угла и времени по расчетной формуле

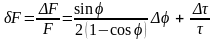, (7)

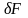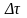где – относительная ошибка измерений силы удара, , и – абсо­лютные ошибки измерений силы, угла и времени,

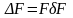. (8)

В формулу (7), как и в формулу (5), ошибку измерений угла следует подставлять в радианах.

Под действием силы энергия шара 2 увеличивается от нуля до вели­чины (2). Таким образом, сила удара совершает работу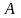 , равную измене­нию энергии шара 2, которая в свою очередь равна :

.

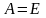Эта работа равна произведению средней силы удара на деформацию шара 2 при соударении с шаром 1,

.

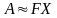Отсюда можно оценить деформацию шара при ударе:

, (9)

где – энергия (2), – сила удара (6).