146.

— 280 —

МОДУЛЬ ІІІ. ЛОГІКА

Тема 4.

УМОВИВІД ЯК ФОРМА РАЦІОНАЛЬНОГО МИСЛЕННЯ

План

1. Загальна характеристика умовиводу.

2. Безпосередні умовиводи.

3. Категоричний силогізм та його різновиди. Ентимема.

4. Полісилогізм.

5. Індуктивні умовиводи. Аналогія.

1. Загальна характеристика умовиводу

Умовивід — це форма мислення, у якій з одного чи кількох іс-тинних суджень на основі певних правил виводу виводять нове суд-ження.

Структура кожного умовиводу включає в себе засновки, вис-новок, логічний зв’язок між засновками та висновком.

Умовивід буде правильним тоді і тільки тоді, коли в ньому вико-нуються основні закони логіки (тотожності, несуперечності, виклю-ченого третього, закон достатньої підстави).

Логічним висновком з цих засновків є таке речення, яке не може бути хибним, коли ці засновки істинні.

Умовиводи поділяються на дедуктивні, індуктивні і умовиводи за аналогією. Вони можуть бути необхідними та ймовірними (прав-доподібними).

Дедуктивний умовивід — це умовивід, у якому висновок зроб-лено обов’язково із засновків, які виражають знання достатньо ве-ликого ступеня загальності, які самі є знанням меншого ступеня за-гальності:

1. усі люди смертні;

2. Сократ — людина;

3. отже, Сократ — смертний.

Логічне слідування іде від роду до виду, від загального класу до підкласу.

Правила виводу повинні задовольняти ряд вимог:

по-перше, з істинних засновків вони повинні давати змогу виво-дити тільки істинні судження;

— 281 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

по-друге, правила виводу в даній логічній системі повинні бути не-суперечними (сумісними), тобто не можна одним способом з одних і тих самих засновків виводити висновок «а», а другим cпособом — «не-а»;

по-третє, необхідно виходити з наявності повноти системи, а це означає: користуючись тільки даними правилами виводу в даній логічній системі, можна вивести будь-які змістово-істинні висновки, які сформульовані в термінах даної системи і логічно випливають з даних засновків.

Правила прямого виводу дають змогу з наявних істинних зас-новків одержати істинний висновок.

Правила непрямого виводу дають змогу робити висновок про правомірність деяких висновків з правомірності інших.

2. Безпосередні умовиводи

Безпосередніми умовиводами називаються дедуктивні умо-виводи, які виводять з одного засновку. До них належать: перетво-рення, обернення, протиставлення предикатові та умовивід за «логіч-ним квадратом».

Перетворення — вид безпосереднього умовиводу, в якому зміню-ється якість засновків без зміни їх кількості. Перетворення будуються:

а) шляхом подвійного заперечення, яке ставиться перед зв’язкою і перед предикатом:

(S є Р S не є не-Р);

б) заперечення переноситься з предиката до зв’язки: (S є не-Р S не є Р).

Перетворенню підлягають усі 4 види суджень А, Е, І, О:

— А Е (Всі S є Р Жодне S не є не-Р);

— Е А (Жодне S не є Р Усі S не є не-Р);

— І О (Деякі S є Р Деякі S не є не-Р);

— О І (Деякі S не є Р Деякі S є не-Р).

Оберненням називається такий безпосередній умовивід, в якому у висновку (новому судженні) суб’єктом стає предикат, а предика-том — суб’єкт. Обернення бувають прості (без обмежень) і з обмежен-нями. Частково заперечні судження не обертаються.

Прості обернення утворюються тоді, коли і S, і Р вихідного су-дження або розподілені, або нерозподілені.

Наприклад: «Деякі студенти — спортсмени. Деякі спортсмени— студенти».

— 282 —

МОДУЛЬ ІІІ. ЛОГІКА

Обернення з обмеженням можна зробити тоді, коли у вихідному судженні суб’єкт є розподіленим, предикат — нерозподіленим або нав-паки — суб’єкт є нерозподіленим, а предикат — розподіленим.

Наприклад: «Всі свині — ссавці. Деякі ссавці — свині». Протиставлення предикатові — такий безпосередній умовивід,

у якому в новому судженні (тобто висновку) суб’єктом виступає по-няття, яке суперечить предикату вихідного судження, а предикатом є суб’єкт вихідного судження, причому зв’язка змінюється на протилеж-ну. Алгоритмом для отримання висновку категоричного судження є:

— замість Р беремо не-Р,

— міняємо місцями S і не-Р,

— зв’язку міняємо на протилежну.

Інакше кажучи, для протиставлення предикатові треба спочатку зробити з судженням перетворення, а потім — обернення.

Наприклад: «Всі вовки — хижі тварини, Жодна нехижа тварина не є вовком».

В абстрактному плані:

Для А — Всі S є Р Жодне не-Р не є S; Для Е — Жодне S не є Р Деякі не-Р є S; Для О — Деякі S не є Р Деякі не-Р є S;

Для І — з частково ствердного судження необхідні висновки не робляться.

Умовиводи за «логічним квадратом» будуються на основі спів-відношення А, Е, І, О.

3. Категоричний силогізм та його різновиди. Ентимема

Категоричний силогізм — це вид дедуктивного умовиводу, в яко-му з двох категоричних суджень, зв’язаних середнім терміном (М), при додержанні правил обов’язково випливає висновок. У складі си-логізму обов’язково повинні бути два засновки і висновок.

Поняття, що входять до складу силогізму, називають його тер-мінами.

Більший засновок має в собі більший за обсягом термін, менший засновок — менший термін.

В основі висновку в категоричному силогізмі лежить аксіома си-логізму. Все, що стверджується або заперечується стосовно виду (або члена даного класу), належить до даного роду.

— 283 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

Фігурами силогізму називаються форми силогізму, які розрізня-ються за положенням середнього терміна М у засновках. Розрізняють 4 фігури силогізму:

Особливі правила фігур:

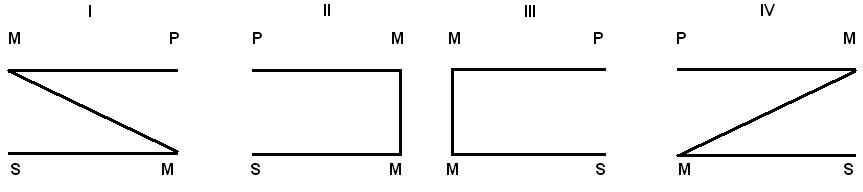
І фігура: більший засновок повинен бути загальним, а менший — ствердним.

ІІ фігура: більший засновок є загальним, а один із засновків і вис-новок — заперечними.

ІІІ фігура: менший засновок повинен бути ствердним, а висно-вок—частковим.

IV фігура: загальноствердних висновків не дає; якщо більший засновок ствердний, тоді менший повинен бути загальним.

Якщо один із засновків заперечний, то більший повинен бути за-гальним.

Модусами категоричного силогізму називаються його різновиди, що відрізняються один від одного якісною й кількісною характерис-тикою засновків, що входять до нього, і висновком. Всього правиль-них модусів у 4 фігурах — 19.

Правила для термінів категоричного силогізму:

— в кожному силогізмі повинно бути тільки 3 терміни (S, Р, М);

— середній термін (М) повинен бути розподілений хоча б в од-ному із засновків;

— термін, не розподілений у засновку, не може бути розподіле-ним у висновку.

Правила для засновків категоричного силогізму:

— з двох заперечних засновків не можна зробити ніякого вис-новку;

— якщо один із засновків заперечний, то й висновок повинен бу-ти заперечним;

— з двох часткових засновків висновку робити не можна;

— 284 —

МОДУЛЬ ІІІ. ЛОГІКА

— якщо один із засновків частковий, то й висновок повинен бути частковим.

Ептимемою називається скорочений категоричний силогізм, в якому пропущений один із засновків або висновок.

Наприклад: «Олександр вивчає філософію, оскільки він сту-дент». Тут пропущений більший засновок. «Усі студенти вивчають філософію».

Відновлений з ентимеми силогізм має такий вигляд: Усі студен-ти вивчають філософію. Олександр — студент.

Отже, Олександр вивчає філософію.

4. Полісилогізм

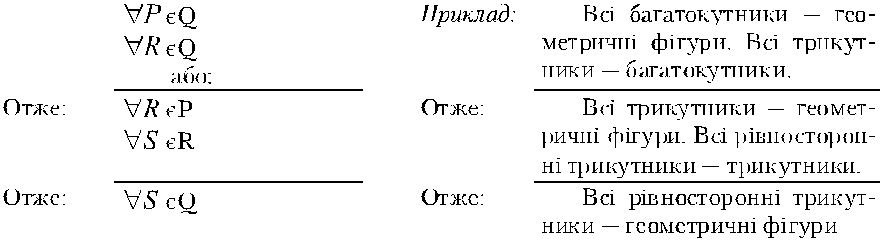
Полісилогізмом (складним силогізмом) називаються два або кілька простих категоричних силогізмів, пов’язаних один з одним так, що висновок одного з них є засновком для іншого.

У полісилогізмі висновок попереднього силогізму стає більшим засновком наступного силогізму. Його схема:

— 285 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

5. Індуктивні умовиводи. Аналогія

Індуктивні умовиводи — це опосередковані умовиводи, у яких з одиничних суджень — засновків — виводять часткове або й загальне судження — висновок. Слід відзначити, що індукція може виступати у науковому пізнанні подвійно — як метод та як логічний висновок. У якості методу вона виступає правилом наукової діяльності окремого ученого або цілого наукового співтовариства. У формі логічних ви-сновків ця процедура виражає себе, як правило, — однією з активнос-тей суб’єкта, який пізнає.

Звичайно виділяють два основні смисла поняття «індукція»: 1) індукція як узагальнення, 2) індукція як імовірний висновок. Існують наступні види індукції:

— Математична індукція;

— Перечислювальна (енумеративна) індукція;

— Еліминативна індукція;

— Індукція как зворотня дедукція;

— Аналогія;

— Логічна індукція.

Математична індукція — індукція як узагальнення, яка є до-стовірним (не імовірним) висновком. Ступінь достовірності цього виду висновків здавалась деяким мислителям настільки значною, що передбачалося розглядати математичну індукцію як одну з аксіом формальної логіки.

Загальну схему аксіоми математичної індукції можна було б зо-бразити у наступному вигляді:

Властивість Р вірна для 1

Якщо властивість Р вірна для n, то Р вірна для (n+1)

______________________________________________________________________________________

Властивість Р вірна для n

Перечислювальна (енумеративна) індукція. У індуктивному висновку мислитель має справу із певним класом об’єктів. Цей клас містить звичайно дуже велику кількість об’єктів, які усі практично неможливо дослідити. Далі з’ясовується, що певне кінцеве число об’єктів має певну властивість Р. На цій підставі дослідник може із певної ймовірністю передбачити, що властивість Р виконується для усіх об’єктів класу. Отримуємо наступну загальну формулу енумера-тивної індукції:

— 286 —

МОДУЛЬ ІІІ. ЛОГІКА

1-й об’єкт о₁ класу К володіє властивістю Р 2-й об’єкт о₂ класу К володіє властивістю Р

n-й об’єкт о_n класу К володіє властивістю Р

_________________________________________________________________________

Всі об’єкти класу К володіють властивістю Р

Тут розрізнюють два випадки:

• Клас усіх об’єктів К вичерпується множиною F, тобто у посил-ках ми перевірили володіння властивістю Р для усіх об’єктів класу

0. Наприклад, ми стверджуємо властивість «бути молодше 20 років» для усіх учнів певного класу. Якщо у класі , наприклад, 17 осіб, то для кожного з них ми можемо визначити вік, установивши, що він менше 20 років, а потім перейти до висновку, що «Усі учні класу молодше 20 років». Такий вид перечислювальної індукції називається повною пе-речислювальною індукцією, оскільки множина F повністю вичерпує собою досліджуємий клас К.

2. Клас усіх об’єктів К не вичерпується множиною F, наприклад, К може бути нескінченною множиною, тоді як множина F завжди утримує тільки кінцеве число елементів. Цей вид перечислювальної індукції називається неповною перечислювальною індукцією. Тут ми вже здійснюємо стрибок у мисленні, переходячи від виконання властивостей Р на частині класу К до виконнання цієї властивості на цілому класі К. Через цей стрибок можливі помилки, коли у зали-шившейся частині К може знайтися об’єкт, який ще не перевірений на володіння властивістю Р й найсправді такою властивістю не воло-діє. Наприклад, ви стоїте на зупинці і чекаєте автобуса № 3. Першого разу підійшов автобус № 2 (автобус № 3 не підійшов у момент t₁), потім підійшов автобус № 7 (автобус № 3 не підійшов у момент t₂), Потім — 11 (автобус № 3 не підійшов у момент t₃). У розпачі ви гото-ві зробити індуктивний висновок «Автобус № 3 ніколи не підійде», і раптом радісно помічаєте автобус № 3. Тому неповна перечислю-вальна індукція — це тільки ймовірний висновок.

Аналогія. У випадку висновку за аналогією звичайно дані два об’єкта і безліч властивостей (на відміну від перечислювальної індук-ції, де дана одна чи дві властивості і безліч об’єктів). Можна сказа-ти, що перечислювальна індукція — це узагальнення по об’єктах, коли фіксуються властивості і змінюється множина об’єктів, а аналогія — узагальнення по властивостям, коли навпаки, фіксуються об’єкти і змінюється множина властивостей. Розглянемо наступний приклад

— 287 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

аналогії. Людина стверджує, що на Марсі є життя, оскільки на Марсі, як і на Землі, є атмосфера, вода тощо. Такий висновок можна було представити наступним чином. Позначимо судження:

« На Землі є атмосфера» — як А(з); «На Землі є вода» — як В(з);

«На Землі перепад температур у межах Т» — як Т(з); «На Землі перепад сили ваги у межах F» — як F(з); «На Землі є життя» — як Ж(з); «На Марсі є атмосфера» — як А(м); «На Марсі є вода» — як В(м);

«На Марсі перепад температур у межах Т» — як Т(м); «На Марсе перепад сили ваги у межах F» — як F(м); «На Марсі є життя» — як Ж(м).

Тоді висновок за аналогією може бути представлений у наступ-ному вигляді:

А(з), В(з), Т(з), F(з), Ж(з)

А(м), В(м), Т(м), F(м)

___________________________________________

Ж(м)

Як і неповна перечислювальна індукція, аналогія є ймовірним ви-сновком. Існує проста аналогія, у якій на підставі подібності предме-тів за одними якими-небудь ознаками роблять висновок про їх поді-бність в інших ознаках. Є також строга аналогія, яка ґрунтується на знанні залежності ознак предметів, що порівнюються, й нестрога ана-логія, у якій робиться висновок без знання про зв’язок подібних ознак.

Варто відзначити, що проблема індукції як особливої мисли-тельної операції до цих пір приховує безліч неоднозначностей. Деякі філософи, наприклад, К. Поппер, взагалі заперечували індукцію як засіб і метод наукової діяльності. Ймовірно, справа тут у великому значенні додаткових методів обгрунтування, необхідних для повного використання індукції.

В логіці існують також опосередковані дедуктивні умовиводи. Проведемо логічний аналіз наступного міркування: Якщо число поді-ляється на 4, то воно поділяється і на 2. Число поділяється на 4. Отже, воно поділяється і на 2. У формалізованому вигляді цей висновок записується так:

.

— 288 —

МОДУЛЬ ІІІ. ЛОГІКА

У традиційній логіці такий висновок називається умовно-катего-ричним силогізмом, оскільки перша посилка тут — умовна, друга — категоричне судження.

Взагалі складні опосередковані дедуктівні умовиводи розрізня-ють, виходячи із того які судження складають посилки.

ТАБЛИЦЯ ІНШИХ ВИДІВ ОПОСЕРЕДКОВАНИХ ДЕДУКТИВНИХ УМОВИВОДІВ

№

Назви умовиводів Формули

п/п

1 Суто умовний умовивід

• Умовно-категоричні умовиводи:

2.1 Стверджуючий модус

2. Заперечуючий модус

3 Розділово-категоричні умовиводи:

3.1 Стверджуючо-заперечуючий мо дус (Більший засновок — завжди строга ₁₎ диз’юнкція)

3.2 Заперечуючо-стверджуючий модус (Більший засновок — як строга, так ²⁾ і нестрога диз’юнкція)

4 Умовно-розділові умовиводи:

1. Проста конструктивна дилема

4.2 Складна конструктивна ди лема

3. Проста деструктивна дилема

3. Складна деструктивна дилема

— 289 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

Запитання та завдання для самоконтролю

1. Що таке умовиводи?

2. Які існують умовиводи?

3. Поясніть структуру силогізму.

4. Назвіть основні модуси і структури силогізму.

5. Які існують основні помилки при побудові силогізму?

Теми для написання рефератів

1. Силогізм, його функція в логіці Арістотеля.

2. Умовивід та його роль в мисленні людини.

3. Умовивід і судження як форма відображення дійсності.

4. Умовно-категоричний силогізм в логіці.

Література

1. Гетманова А. Д. Логика: Словарь и задачник: Учебн. пособие для ВУЗов. — М.: Гуманитарное изд. Центр ВЛАДОС, 1998. — С. 194–227.

2. Гетманова А. Д. Логика: Учебник для студентов пед. ВУЗов. — М.: Высшая школа, 1986. — С. 110–130.

3. Ивин А. А. Логика: Учебник для ВУЗов. — М.: Гардарика, 1999. —

148–153.

— 290 —

МОДУЛЬ ІІІ. ЛОГІКА

КОНТРОЛЬНІ МОДУЛЬНІ ЗАВДАННЯ

ВАРІАНТ 1

• РІВЕНЬ

0. Визначте вид відношення між поняттями «майор» і «лей-тенант»:

а) відношення рівнозначності (тотожності); б) відношення підпорядкування;

в) відношення перетинання (перехрещення або часткового збіру);

г) відношення співпорядкування.

0. Поняття «аполітичний» є:

а) позитивним; б) негативним.

0. Перехід від поняття «тварина» до поняття «дика твари-на» є:

а) узагальненням поняття; б) обмеженням поняття.

0. Судження «Цигани шумною юрбою по Бесарабії кочують» є:

а) загальноствердним судженням(А); б) загальнозаперечним судженням (Е); в) частковоствердним судженням (І); г) частковозаперечним судженням (О).

0. Знайдіть поняття:

а) Я поспішаю?

б) Розумна людина; в) Ви хворієте.

0. Обсяг поняття «нація» є:

а) одиничний; б) загальний.

— 291 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

7. Будь-яке поняття має:

а) обсяг; б) розмір; в) фігуру.

7. Одиничним є поняття:

а) пустеля; б) вогонь; в) Геракліт.

7. Знайдіть судження:

а) велике свято; б) студент склав іспит; в) Україна.

10. Алюміній — тверде тіло; залізо, мідь, цинк, срібло, платина, золото, нікель, барій, калій, свинець — також є твердими тілами; отже всі метали — тверді тіла. Це міркування є:

а) індуктивним; б) дедуктивним;

в) міркуванням за аналогією.

2-Й РІВЕНЬ

1. Знайдіть поняття, що є тотожніми за обсягом до наведених (не використовуйте власні імена):

а) рівносторонній трикутник; б) прямокутний ромб.

2. Знайдіть декілька понять, які були б співпідпорядкованими до наведених (по відношенню до деякого третього родового поняття):

а) тварина; б) поняття.

3-Й РІВЕНЬ

1. Що таке класифікація і які види існують?

2. Які існують помилки у визначенні понять? Охарактеризуйте їх.

3. Наведіть приклади суттєвих родових та суттєвих видових ознак.

— 292 —

МОДУЛЬ ІІІ. ЛОГІКА

ВАРІАНТ 2

• РІВЕНЬ

0. Визначте вид відношення між поняттями «кішка» і «со-бака»:

а) відношення рівнозначності (тотожності) б) відношення підпорядкування;

в) відношення перетинання (перехрещення або часткового збору);

г) відношення співпідпорядкування.

0. Поняття «злоба» є:

а) позитивним; б) негативним.

0. Перехід від поняття «дика тварина» до поняття «твари-на» є:

а) узагальненням поняття; б) обмеженням поняття.

0. Судження «Окремі студенти не склали іспит» є:

а) загальноствердним судженням(А); б) загальнозаперечним судженням (Е); в) частковостверднм судженням (І); г) частковозаперечним судженням (О).

0. Знайдіть поняття:

а) олімпійський чемпіон; б) гроші скінчилися; в) погода просто чудова.

0. Обсяг поняття «столиця» є:

а) одиничний; б) загальний?

0. Будь-яке поняття має:

а) фігуру; б) зміст; в) розмір.

— 293 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

8. Загальним є поняття:

а) Г. Гегель; б) філософ.

8. Знайдіть судження:

а) всі хірурги — лікарі. б) чудовий лікар; в) пекельний дух.

10. Будь-яка рідина є рідкою; вода — це рідина; отже, вода є рідкою. Це міркування є:

а) індуктивним; б) дедуктивним;

в) міркуванням за аналогією.

2-Й РІВЕНЬ

1. Знайдіть поняття, що є тотожними за обсягом до наведених (не використовуйте власні імена):

а) столиця Литви; б) друга голосна літера української абетки.

2. Знайдіть декілька понять, які були б співпідпорядкованими до наведених (по відношенню до деякого третього родового поняття):

а) аналіз; б) співпідпорядкування понять.

3-Й РІВЕНЬ

1. У чому полягає сутність операції визначення понять?

2. Що таке міркування? Яка його структура?

3. У чому полягає специфіка формалізованих мов?

— 294 —

МОДУЛЬ ІІІ. ЛОГІКА

ВАРІАНТ 3

• РІВЕНЬ

0. Визначте вид відношення між поняттями «гроші» і «бруд-ні гроші»:

а) відношення рівнозначності (тотожності); б) відношення підпорядкування;

в) відношення перетинання (перехрещення або часткового збіру);

г) відношення співпідпорядкування;

0. Поняття «безкорисливий» є:

а) позитивним; б) негативним.

0. Перехід від поняття «людина» до поняття «розумна лю-дина» є:

а) узагальненням поняття; б) обмеженням поняття.

0. Судження «Деякі з нас здатні витримати ще й не таке ви-пробування» є:

а) загальноствердним судженням(А); б) загальнозаперечним судженням (Е); в) частковоствердним судженням (І); г) частковозаперечним судженням (О).

0. Істинним або хибним може бути:

а) поняття; б) судження; в) термін.

0. Знайдіть судження:

а) складний залік; б) група склала залік;

в) найскладніший залік у моєму житті.

0. У структуру простого судження не входить:

а) суб’єкт;

— 295 —

ФІЛОСОФІЯ. КРЕДИТНО-МОДУЛЬНИЙ КУРС

б) префикат; в) силогізм.

8. «Дехто зі студентів не склав залік з логіки». Це судження:

а) просте; б) складне.

8. Визначте тип судження «якщо число парне, воно ділить-ся на два»:

а) конюнкція; б) імплікація; в) еквіваленція.

10. «Прямокутник — це плоска геометрична фігура, в якої протилежні сторони однакові і паралельні, а всі кути — прямі. Квадрат також є плоскою геометричною фігурою з однаковими і паралельними протилежними сторонами. Отже, всі кути квадрату — прямі». Це міркування є:

а) індуктивним; б) дедуктивним;

в) міркуванням за аналогією.

2-Й РІВЕНЬ

1. Які з наведених прикладів фіксують відношення роду і виду, а які виражають відношення частини і цілого?

а) Школа. Середня школа; б) Україна. Європа.

2. Знайдіть декілька понять, які були б співпідпорядкованими до наведених (по відношенню до деякого третього родового поняття):

а) прикметник; б) обличчя.

3-Й РІВЕНЬ

1. Які види визначень Ви знаєте? Наведіть відповідні приклади.

2. Як можна відрізнити правильне міркування від неправильно-го? Обґрунтуйте відповідь.

3. Яка мета створення формалізованих мов?

— 296 —

МОДУЛЬ ІІІ. ЛОГІКА

ВАРІАНТ 4

• РІВЕНЬ