Затухающие колебания. Резонанс.

238. Определить коэффициент затухания и время релаксации математического маятника, если за промежуток времени t=480 с маятник теряет 99 % своей полной механической энергии.

239. Логарифмический декремент затухания математического маятника равен 0,2. Найти, во сколько раз уменьшиться амплитуда колебаний за одно полное колебания маятника.

240. Тело массой m=12 г совершает затухающие колебания с частотой w=p рад/с. При этом за время t=60 с тело теряет 0,9 своей полной механической энергии. Найти: a) коэффициент затухания; б) коэффициент сопротивления среды; в) добротность колебательной системы.

241. Логарифмический декремент затухания математического маятника равен 0,4. Найти, во сколько раз уменьшиться амплитуда колебаний за два полных колебания маятника.

242. Тело массой m=360 г подвешено к пружине с коэффициентом жесткости k=16 Н/м и совершает вертикальные колебания в некоторой среде. Логарифмический декремент затухания . Сколько колебаний N должно совершить тело, чтобы амплитуда смещения уменьшилась в е раз? За какой промежуток времени произойдет это уменьшение амплитуды?

243. Затухающее колебание описывается уравнением . Определите время релаксации, период колебаний, коэффициент затухания, добротность.

244. Затухающее колебание описывается уравнением . Определите время релаксации, период колебаний, коэффициент затухания, добротность.

245. Частица совершает прямолинейные затухающие колебания с периодом Т=4,5 с. Начальная амплитуда колебаний А₀=0,16 м, а амплитуда после 20 полных колебаний А=0,01 м. Определить коэффициент затухания и логарифмический декремент затухания. Написать уравнение колебаний частицы, приняв начальную фазу колебаний j=0.

246. Логарифмический декремент затухания математического маятника равен 0,05. Найти, во сколько раз уменьшиться полная энергия колебаний за время t=10T.

247. Математический маятник совершает затухающие колебания в среде, логарифмический декремент затухания которой l=1,26. Определить логарифмический декремент затухания маятника, если сопротивление среды возрастает в 2 раза.

248. Определить амплитуду А вынужденных колебаний груза массы m=0,1 кг на пружине с коэффициентом жесткости k=10 Н/м, если на груз действует вертикальная вынуждающая гармоническая сила с амплитудой F₀=1,5 Н и частотой, в два раза большими собственной частоты груза на пружине. Коэффициент затухания b=0,4с^-1.

249. Найти коэффициент затухания и логарифмический декремент затухания математического маятника, если известно, что за t=100 с колебаний полная механическая энергия маятника уменьшилась в десять раз. Длина маятника L=0,98 м.

250. Амплитуда затухающих колебаний математического маятника за 1 минуту уменьшилась вдвое. Во сколько раз она уменьшится за 3 минуты?

251. Доказать, что резонансная частота колебаний для амплитуды смещения определяется по формуле .

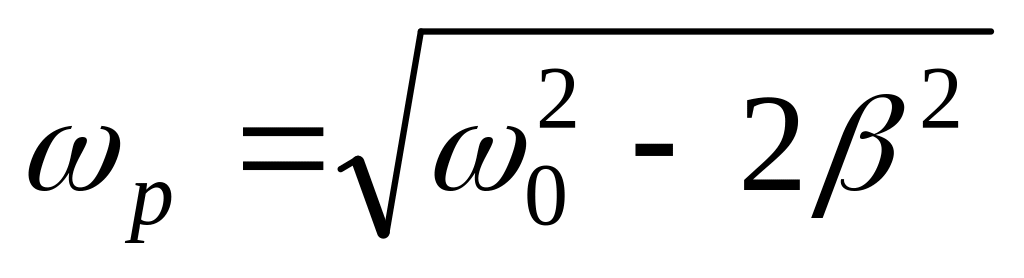252. Доказать, что резонансная частота колебаний для амплитуды скорости определяется по формуле .

253. Доказать, что резонансная частота колебаний для смещения определяется по формуле .

254. Амплитуды смещений вынужденных колебаний при частотах вынуждающей силы 100 и 150 Гц равны между собой. Найти частоту, соответствующую резонансу смещений. Вынуждающая сила изменяется по гармоническому закону.

255. Амплитуды ускорения вынужденных колебаний при частотах вынуждающей силы n₁ и n₂ равны между собой. Найти частоту, соответствующую резонансу ускорения. Вынуждающая сила изменяется по гармоническому закону.

256. Амплитуды скорости вынужденных колебаний при частотах вынуждающей силы n₁ и n₂ равны между собой. Найти частоту, соответствующую резонансу скорости. Вынуждающая сила изменяется по гармоническому закону.

257. Частица совершает прямолинейные затухающие колебания с периодом Т=4,5 с. Начальная амплитуда колебаний А₀=0,16 м, а амплитуда после 20 полных колебаний А=0,01 м. Определить коэффициент затухания и логарифмический декремент затухания. Написать уравнение колебаний частицы, приняв начальную фазу колебаний j=0.

258. Уравнение затухающих колебаний дано в виде м. Найти скорость колеблющейся точки в моменты времени: 0, Т, 2Т, 3Т и 4Т.

259. Амплитуда затухающих колебаний математического маятника за 1 минуту уменьшилась втрое. Во сколько раз она уменьшится за 4 минуты?

260. Тело массой m=360 г подвешено к пружине с коэффициентом жесткости k=16 Н/м и совершает вертикальные колебания в некоторой среде. Логарифмический декремент затухания l=0,01. Сколько колебаний N должно совершить тело, чтобы амплитуда смещения уменьшилась в е раз? За какой промежуток времени произойдет это уменьшение амплитуды?

261. Полная энергия затухающих колебаний математического маятника за 1 минуту уменьшилась вдвое. Во сколько раз она уменьшится за 4 минуты?

262. Логарифмический декремент затухания математического маятника равен 0,1. Найти, во сколько раз уменьшиться полная энергия колебаний за время t=4T.

263. Найти коэффициент затухания и логарифмический декремент затухания математического маятника, если известно, что за t=50 с колебаний полная механическая энергия маятника уменьшилась в десять раз. Длина маятника L=0,98 м.