1.5. Понятие о напряжении

После определения и построения эпюр внутренних шести силовых факторов в сопротивлении материалов переходят к оценке прочности конструкции в точке. Для оценки уровня внутренних усилий в точке (например, т. D на рис. 1.6) вво­дится понятие меры интенсивности внутренних усилий, кото­рая называется напряжением. Под напряжением понимается усилие, отнесенное к единице площади сечения. выделим одну из них площа­дью ДА около точки D; (рис.1.6)

Проиллюстрируем это следующим образом:

— разделим проведенное через т. D сечение на большое чис­ло маленьких площадок (рис. 1.6);

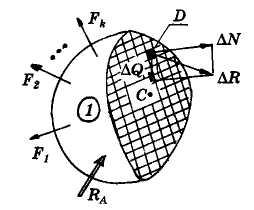
Рис. 1.6. Схема оценки интенсивности

внутренних усилий в точке

- выделим одну из них площа­дью А около точки D; разложим R на нормальную N и касательную Q составляющие усилий в точке.

-пусть R — будет равнодей­ствующей внутренних усилий, при­ходящихся на эту площадку

Тогда средним нормальным напряжением в точке D в пределах площадки А будет , (1.1)

а средним касательным напряжением . (1.2)

В пределе при бескончно большом количестве площадок и при стягивании площади к точке D имеем нормальное напряжение в точке

, (1.3)

касательное напряжение в точке

. (1.4)

Понятие напряжение в точке связано как с самой точкой, так и с положением площадки, проведенной через данную точ­ку. Касательное и нормальное напряжения в смысле точки и площадки взаимосвязаны и не могут рассматриваться отдельно друг от друга. Это составляющие одного физического понятия.

В отличие от скалярных и векторных величин, понятие напряжения в точке относится к тензорам, т.е. физическим величинам, преобразующимся по опреде­ленному закону при переходе от одной системы координат к другой.

Совокупность нормальных и касательных напряжений для множества элементарных площадок, проходящих через точ­ку, характеризует напряженное состояние в точке. Сущность метода расчета на прочность по допускаемым напряжениям состоит в нахождении этих напряжений, определении их эк­стремальных (наибольшего и наименьшего значений) величин.

1.6. Понятие о деформациях

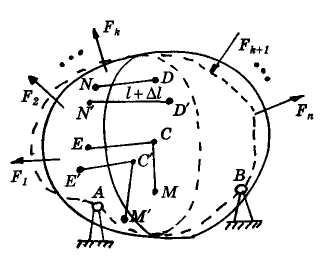Под действием системы внешних сил (а также реакций свя­зи) конструкция изменяет свои первоначальные размеры (иног­да и форму). Для того, чтобы охарактеризовать интенсивность изменения размеров и формы тела при нагружении рассмот­рим точки N и D недеформированного тела, находящиеся друг от друга на расстоянии I (рис. 1.7).

Рис. 1.7

Схема деформации тела под нагрузкой

Предположим, что после нагружения в результате дефор­мации эти точки займут положения N' и D', а расстояние l увеличится на . Предел отношения приращения длины от­резка к его первоначальной длине называют мерой линейной деформации отрезка в точке D, или относительной дефор­мацией (в направлении ND): . (1.5)

Деформации в направлении декартовых осей координат обо­значаются как ε_х, ε_у, ε_z. При прочностном анализе вводится по­нятие угловой деформации. Пусть в недеформированном теле отрезки ЕС и СМ образуют прямой угол. После нагружения и деформирования тела угол ∟ECM изменяется и принимает значения ∟E'C'M'.

Углом сдвига или угловой деформацией в точке С плоско­сти СЕМ называется предел разности углов ECM и E'C'M' при стягивании точек Е и М к точке С:

. (1.6)

Совокупностью линейных ε_х, ε_у, ε_z и угловых деформаций γ_xy> γ_yz> γ_хz по всем возмож­ным направлениям и плос­костям можно охарактери­зовать деформированное состояние в исследуемой на прочность точки тела при на­гружении.