4.4 Визначення довірчих інтервалів коефіцієнтів множинної регресії

Останнім, завершаючим етапом аналізу моделі множинної регресії є оцінка довірчих інтервалів отриманих коефіцієнтів моделі. Справа у тому, що визначені одного разу коефіцієнти моделі системи не будуть незмінними при їх повторному визначенні із застосуванням нових експериментальних даних, а кожного разу їх значення будуть відрізнятися від попередніх значень. Задачею цього розділу буде саме визначення границь інтервалів, в яких з заданою ймовірністю будуть знаходиться вказані коефіцієнти при їх повторних визначеннях.

В теорії статистики доведено, що отримані оцінки коефіцієнтів моделі, будуть незміщеними і обгрунтованими при виконанні наступних умов:

- при кожному спостереженні похибка є випадковою величиною з математичним сподіванням М_ε=0 і дисперсією тобто систематична складова похибки відсутня.

- матриця значень складається з лінійно - незалежних змінних.

Саме при виконанні цих умов дисперсія параметрів моделі визначається матрицею коваріацій вектора оцінок А:

З огляду на (4.13):

;

де Е- одинична, діагональна матриця, матриця коваріацій (дисперсій) параметрів моделі регресії А прийме вид :

Приймаючи замість його оцінку S², яка визначається як

де (п-т) - число ступенів свободи, яке дорівнює числу вибірок за винятком числа параметрів моделі, що визначаються, маємо:

(4-14)

де - діагональні елементи матриці

Тоді середньо-квадратична помилка визначення параметра а_j буде дорівнювати

(4.15)

Формули (4.14) і (4.15) можуть бути використані безпосередньо для оцінки параметрів моделі множинної регресії.

У розглянутому вище прикладі діагональні елементи матриці (Х'Х)'¹ є рівними:

; ;

Розрахуємо S²:

Тоді середню квадратичну похибку визначення а, розрахуємо по (4.14) з урахуванням (4.15):

Далі визначимо розрахункові коефіцієнти довіри (t- коефіцієнти) для параметрів моделі: ; ;

При рівні довірчої ймовірності Р=0,95 і числі ступенів свободи К=п-

m-1=19-2-1=16 по таблиці Стьюдента знаходимо критичне значення коефіцієнта довіри =2,12. Тому в отриманому рівнянні регресії, значущим є лите коефіцієнт регресії ⁼1,532, тобто вплив змінної є незначним.

Довірчий інтервал для коефіцієнта моделі а₂ визначається (при p=0,95):

Оскільки параметри а_о і а₁ не є значущими, то а₁ може бути виключений з рівняння множинної регресії. При цьому замість змінної х може бути прийнята друга змінна, яка досі не розглядалась і не була введена в модель множинної регресії. Можливо, що ця подія допоможе підвищити точність моделі. Але при цьому всю процедуру оцінюваная необхідно повторити з усіма експериментальними даними, включаючи також дані про нову змінну *|.

Завершуючи розгляд методики отримання моделей множинної лініійної регресії, введемо програму розрахунків коефіцієнтів множинної регресії та оцінку точності моделі у середовище MATHCAD -2000 (див. нижче).

В наведеній програмі досліджується залежність прибутку (у) від обсягу капіталовкладень за поточний рік (х,), обсягів основних фондів (x-) і чисельності працюючих на 7 аналогічних підприємствах.

Отриманий коефіцієнт детермінації К_а =0,922 свідчить про те, що незалежні змінні (аргументи моделі) вибрані правильно. Про це свідчить також і отримана дисперсія похибки моделі.

Зауважимо, що в результаті розрахунків чисельність працюючих негативно впливає на прибутковість роботи підприємств. Виходячи з цього необхідно приділити значну увагу саме питанню більш ефективного використання особистого складу працюючих з метою підвищення їх віддачі. Можливо, що необхідно скоротити адміністративний персонал і підвищити долю безпосередньо зайнятих на виробництві людей.

Задання вихідних даних

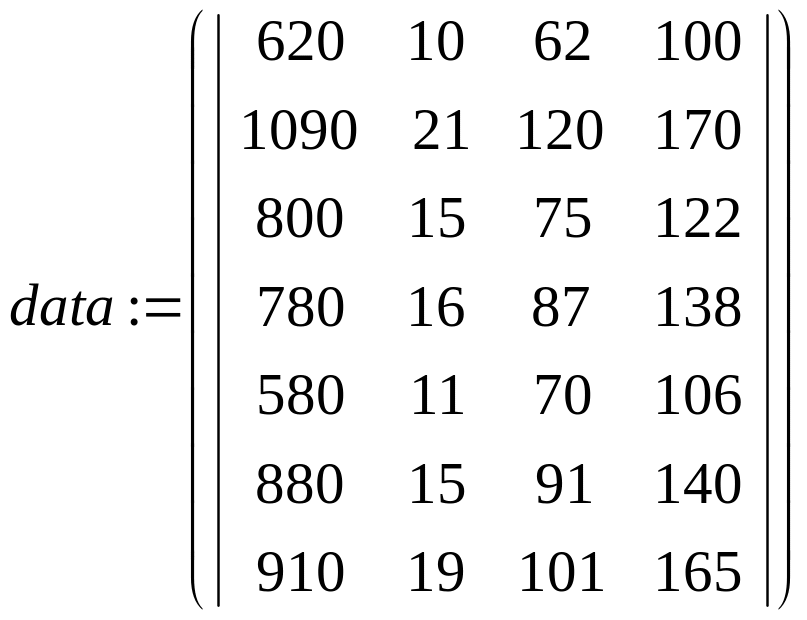
; ; k:=1

Результати розрахунків коефіцієнтів моделі:

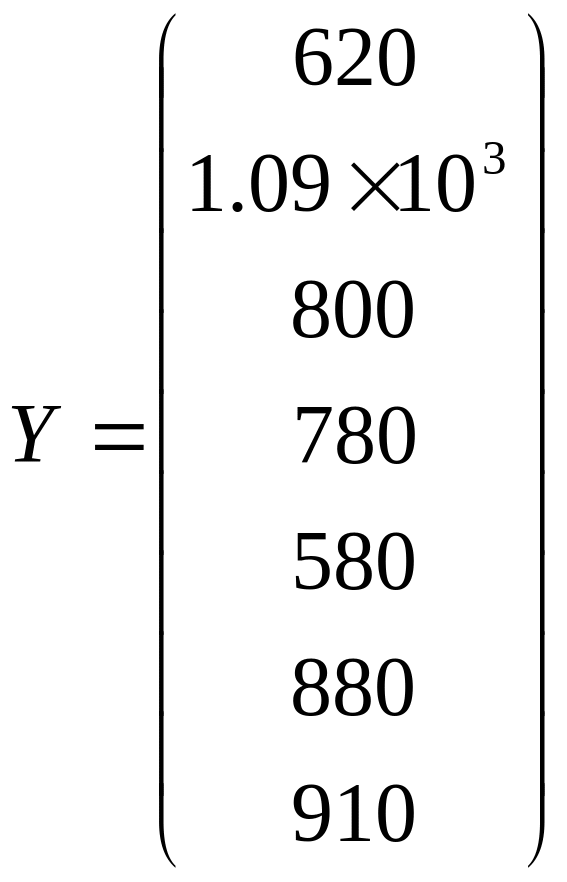
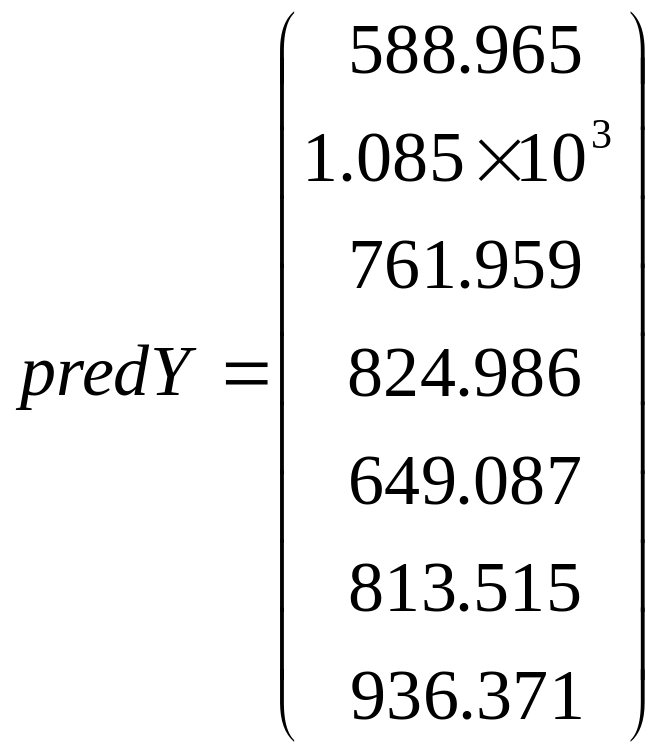
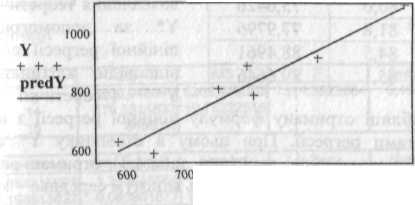
resid := predY- Y _sca|e ._{= max}(|«,„,)).,.,

Residuals vs. Y

		1 1 і	1
я				-
		+		0
0	"--■			1
-50	+			_
	І	і 1 +І	1

500 600 700 800 900 1000 1100

Сумісне графічне представлення регресійного поля та лінійної моделі регресії