4.3 Аналіз моделі множинної регресії

Як видно з отриманого рівняння моделі, вплив оборотних коші і валовий доход майже в 10 разів більший, ніж обсяг основних фондів, і відображає реалії ринку: «живі гроші дають більший і швидкий чим вкладання в розвиток виробництва. Однак не слід забувати, що ' порівняння можливе лише при однаковій розмірності незалежних змій (наприклад х₁ і х₂ виражені в тис. гривень, але не в тисячах і мільйонах гривень). Так само не можна порівнювати ці впливи при різному фізичному змісті змінних. Наприклад, якщо х₁- інтенсивність руху (авт/год.), а х₂ - ширина проїзної частини (м), то співвідношення а₁ і а₂ взагалі не може служити мірою порівняння ступеня впливу цих параметрів на у- пропускну здатність автомобільної дороги.

Однак, щоб зробити можливим порівняння коефіцієнтів регресії й оцінити вник, щоб зробити можливим порівняння коефіцієнтів регресії й підносний відносний вплив змінних х_j на у^с у відносних одиницях, застосовують нормування коефіцієнтів регресії (α_j).

Коефіцієнт α_j показує величину змін в значення СКО величини у при зміні на одне СКО величини х_j, тобто

α_j = α_j(σ_xj/σ_y)

де σ_y=√1/N*(y_i-y^c)² σ_xj=√1/N*(x_i-x^c)²

Зокрема, для розглянутого прикладу: σ_x1=54,05; σ_x2=22.36; σ_y=55.91; x₁^c=71.69; x₂^c=71.69; =95.489; α₁=0.194; α₂=0.647;

У такий спосіб відносний вплив x₂ на виявився більшим лише в α₁/ α₂= 0.647/0.194=3, 3 рази.

Для статистичної оцінки тісноти зв’язку застосовуються, як і в рівняннях парної регресії, ті ж самі три показники варіацій і коефіцієнти тісноти зв’язку, що базуються на них.

Основні показники варіації:

1. Загальна дисперсія, що відображає сукупні впливи всіх об’єктивно діючих факторів:

2. Факторна дисперсія, що відображає вплив тільки вивчених незалежних змінних:

де - значення , розраховані по моделі, для кожного і-того зі сполучень , що мають місце в даному експерименті

3. Залишкова дисперсія, що відображає вплив неврахованих змінних, (крім х_j j = (l,m));

У цій формулі вираз в дужках показує відхилення експериментальних даних відносно рівняння регресії. Для розглянутого випадку маємо: = 2799.345; =1493.202;

З огляду на те, що = + , одержимо вираз для залишкової дисперсії

= - =1306.143

По величині , зокрема, можна оцінювати точність різних моделей регресії. Відношення 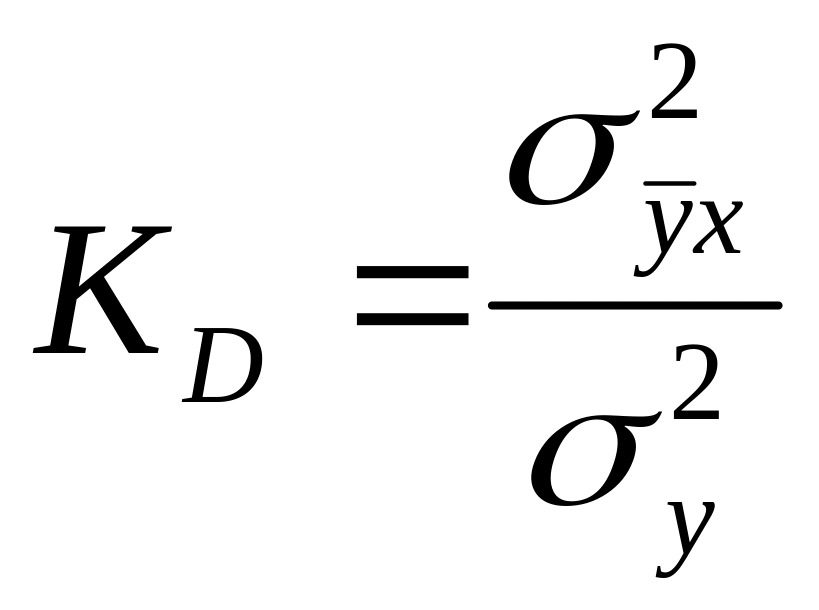у даному випадку є коефіцієнтом множинної детермінації (для нелінійної регресії - індекс детермінації) і характеризує ступінь впливу обраних незалежних змінних на результативну ознаку у. Для розглянутого прикладу

,

тобто 53% мінливості у обумовлені саме мінливістю х₁ і х₂

Тоді коефіцієнт множинної кореляції (для нелінійної регресії індекс кореляції) визначається як

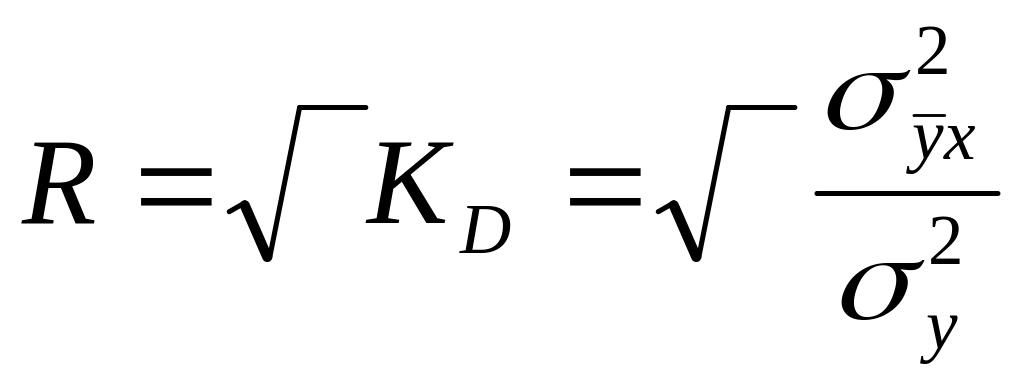
Для розглянутого приклада R=0,73, що свідчить про досить значний взаємозв'язок між у та х₁ і х₂

З огляду на те, що = + , можна одержати трохи зручнішу для практичних розрахунків формулу, яка широко використовується при розрахунках моделей із застосуванням ЕОМ

Неважко показати, що при m=1 (тобто при парній регресії у(х)), це вираження збігається з раніше отриманим вираженням коефіцієнта R для лінійної регресії.

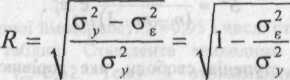
Завершуючи розгляд множинної регресії, приведемо ще одну корисну формулу для розрахунку величини R у матричній формі, що буде використовуватись при розрахунках значення R на ЕОМ: