2.2.2. Вибір форми функціональної залежності

Для визначення форми функціональної залежності будується кореляційне поле y(x_j) для кожної із змінних, що досліджуються. Для цього на осях координат у і х наносяться пари експериментально отриманих значень у_i, та х_i(і =1,N) (Рис.2.2).

Н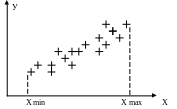 а кореляційному полі знаходяться х_mіn„ та х_mах – мінімальні та максимальні значення незалежної змінної х (саме це і с область, для якої визначаються параметри статистичної моделі).

По характеру розподілення точок кореляційного поля обираються форми функціональної залежності.

Рис. 2.2 Приклад кореляційного поля.

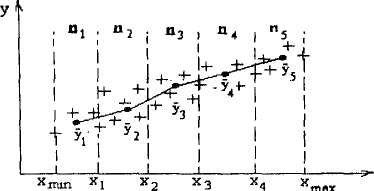
Найбільш простим і наочним являється метод інтервального усереднення. Для цього весь інтервал (від х_min„ до х_max) розбивається на ряд ділянок (зазвичай не більше 7—1), в кожному з яких знаходиться середнє значення змінної у:

(2-4)

де п-число значень у, що потрапили в j-й інтервал х_i (j = 1,n ; n =5...1О).

Рис. 2.3 Інтервальне усереднення даних кореляційного поля.

Отриманні значення у_і співвідносять з серединою j-го інтервалу x_j (див.рис.2.3) отримані точки з'єднують ламаною чи плавною кривою. По характеру отриманої кривої і визначають форму функціональної залежності у (х).

Встановлення форми залежності.

Характер і форма залежності між змінними можуть утворювати наступні різновиди регресії :

- позитивна лінійна регресія(виражається в рівномірному зростанні функції);

- позитивна рівноприскорено зростаюча регресія;

- позитивна равнозамедленно зростаюча регресія;

- негативна лінійна регресія(виражається в рівномірному падінні функції);

- негативна рівноприскорено убуваюча регресія;

- негативна равнозамедленно убуваюча регресія.

Розглянемо деякі припущення, на які спирається регресійний аналіз.

Припущення лінійності, тобто передбачається, що зв'язок між даними змінними є лінійним. Так, в даному прикладі ми побудували діаграму розсіювання і змогли побачити явний лінійний зв'язок. Якщо ж на діаграмі розсіювання змінних ми бачимо явну відсутність лінійного зв'язку, тобто є присутнім нелінійний зв'язок, слід використати нелінійні методи аналізу.

Припущення про нормальність залишків. Воно допускає, що розподіл різниці передбачених і спостережуваних значень є нормальним. Для візуального визначення характеру розподілу можна скористатися гістограмами залишків.

При використанні регресійного аналізу слід враховувати його основне обмеження. Воно полягає в тому, що регресійний аналіз дозволяє виявити лише залежності, а не зв'язки, що лежать в основі цих залежностей.

Регресійний аналіз дає можливість оцінити міру зв'язку між змінними

Найбільш проста і найбільш часто вживана є лінійна модель виду:

у = а + bх, де а = у при х = 0; b = y/x, (2.5)

що є зображеною на рис.2.4. За допомогою цього рівняння змінна Y виражається через константу a і кут нахилу прямої (чи кутовий коефіцієнт) b, помножений на значення змінної X. Константу a також називають вільним членом, а кутовий коефіцієнт b - коефіцієнтом регресії або B- коефіцієнтом.

У більшості випадків (якщо не завжди) спостерігається певний розкид спостережень відносно регресійної прямої, але їх розсіювання відносно даної прямої повинне бути мінімальним. Залишок - це відхилення окремої точки (спостереження) від лінії регресії(передбаченого значення).

Рис.2.4 Графічне тлумачення лінійної моделі

Серед нелінійних моделей часто використовують наступні моделі:

1)Див.рис.2.4а:

(2.6)

для А і В а< 0, b> 0 але |а|_B >|а|_A

для Б і Г а > 0, b > 0 але (а)_Г > (а)_Б

Рис.2.4а

2)Див.рис.2.4б:

y = a x² (2.7)

для А і Б а > 0, 0 < b < 1

для В і Г а > 0, -1< b < 0

3)Див.рис.2.4в: y = a b ^x (2.8)

для А і Б 0 < b < 1; ( b)_А < ( b)_Б

для В і Г b > 1 ; ( b)_Г < ( b)_В

Після вибору форми функціональної залежності проводять лінеаризацію нелінійної моделі (тобто її штучне зведення до лінійної форми)

Наприклад:

у = ab^хlg y = lg a + x lg b  у^’ = а^’ + b^’ x.

y = ax^b lg y = lg a + bgx у^’ = а^’+ b^’ x

і т.п.

Рис.2.4б Часто зручним виявляється використання вихідної таблиці 2.1 експериментальних даних, кодовану по х (за х приймається номер рівномірного інтервалу).

Таблиця 2.1

X	Y	Y	2Y	lпY	lпу	X/У	х/y
	62,1	-	-	1,79246	-	0,01610	-
	87,2	25,1	-	1,93962	-,14716	0,02293	0,0683
	109,5	22,3	-2,8	2,03941	0,09979	0,02739	0,00446
	127,3	17,8	-4,5	2,10483	0,06542	0,03142	0,00403
	134,7	7,4	-10,4	2,12937	0,02454	0,03712	0,00570
	136,2	1,5	-5,9	2,13386	о,оо44<Р	0,04405	0,00693
	134,9	-1,3	-2,8	2,13001	-0,00383	0,05189	0,00784

Розрахуємо різниці, приведені у даній таблиці. Потім оцінимо можливість застосування різних моделей:

у = а + bх.

Ця модель незадовільна, оскільки відношення х/y = y не є постійним.

у = а b^х.

Ця модель приводиться до виду: lg = lg a + х lg b =a^’+ b^’x

Ця модель також незадовільна, оскільки b^’ = непостійне.

у = а + bх + сх²

Ця парабола незадовільна, оскільки непостійне.

Оскільки відношення постійне (при х=1), то цю модель можна

використовувати для апроксимації експериментальних даних.

Поліноміальна модель

У випадку, коли вищерозглянуті моделі не дозволяють знайти задовільну апроксимацію експериментальних даних, часто використовується поліноміальна апроксимація виду:

у = а₀+ а₁ х + а₂ х² + а₃ х³ +... + а_k х^k (2.9)

В залежності від значень а, (і = 0,k ) можливо підібрати досить гарну відповідність моделі і експериментальним даним.

Лінеаризацію моделі даного типу проводять шляхом вводу нових змінних: x₁=х; x₂=х²; х₃=х³; ... x_k=x^k. Тоді поліноміальна модель прийме вид лінійної моделі з k-змінними:

у = а₀+ а₁ х₁^/ + а₂ х^/₂ + ... + а_k х^/_k (2.10)

Такого виду лінійні моделі носять назву моделей множинної лінійної регресії. Далі, при вивченні моделей множинної лінійної регресії ми розглянемо алгоритм пошуку числових значень коефіцієнтів а_i (і= 0,k), що забезпечують мінімальне розсіювання експериментальних даних у відносно значень у, отриманих за допомогою моделі множинної лінійної регресії y(x_i) і = 0,k .

Завершаючи розгляд вибору форми функціональної залежності, відмітимо, що в практиці велика кількість моделей зводиться або до лінійної парної регресії

у = а₀ + bх, або до множинної лінійної регресії y= a₀ + a_i x_i. Тому далі ми розглянемо саме ці моделі.