
- •Методические рекомендации по изучению дисциплины «Математика»
- •Требования к уровню освоения дисциплины «Математика»
- •Контрольные вопросы
- •Контрольные тестовые задания
- •Раздел 1. Линейная алгебра.
- •Раздел 2. Математический анализ
- •!!! Методические указания по выполнению контрольной работы
- •Задания для домашних контрольных работ
- •Рекомендуемая литература
Раздел 2. Математический анализ
Если
 ,
а
,
а  то
то
 равен
равен
а) 5 б) -5 в) 11 г)-24
Если , а то
 равен
равен
а) 11 б) -5 в) 5 г)-24
Если , а то
 равен
равен
а) -24 б) -5 в) 11 г) 5
Если
 ,
а
то
,
а
то
 равен
равен
а) -4 б)-36 в) 9 г) 15
Значение предела
 равно
равно
а)
1 б) х в) ![]() г)
0
г)
0
Значение предела
 равен
равен
а) e б) 1 в) 0 г)
Производной функции y=f(x) в точке х называется предел
а)
отношения приращения функции ![]() к приращению аргумента
к приращению аргумента ![]()
б)
отношения приращения аргумента ![]() к приращению функции
к приращению функции ![]()
Геометрический смысл производной состоит в том, что производная функции y=f(x) в точке
 равна (несколько правильных вариантов
ответов)
равна (несколько правильных вариантов
ответов)
а)
угловому коэффициенту касательной в
точке с координатами ![]()
б) тангенсу угла наклона касательной к графику функции, проведенной в точке , и положительным направлением оси Ох
в)
угловому коэффициенту нормали,
проведенной в точке с координатами ![]()
г) тангенсу угла наклона нормали к графику функции, проведенной в точке , и положительным направлением оси Ох
Механический смысл производной состоит в том, что
а) скорость прямолинейного движения есть производная от пройденного пути по времени
б) ускорение прямолинейного движения есть производная от скорости по времени
в) пройденный путь при прямолинейном движении есть производная от скорости по времени г) скорость прямолинейного движения есть производная от времени
По теореме о пределе частного
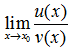 равен
равен
а)
![]() –
конечные пределы и B≠0
–
конечные пределы и B≠0
б)
 в)
в)
 г)
г)
![]()
Если функция в точке а имеет конечную производную, то уравнение касательной имеет вид
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
Производная функции y = ax имеет вид
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Производная функции y = logax имеет вид
а) б) в) г)
Производная функции y = tg x имеет вид
а)
![]() б)
в)
г)
б)
в)
г)
Производная функции y = arcsin x имеет вид
а) б) в) г)
Верными являются следующие свойства неопределённого интеграла (несколько верных вариантов ответа)
а)
![]()
б)
![]()
в)
![]() г)
г)
![]()
Неопределенный интеграл
 равен
равен
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
Неопределенный интеграл
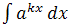 равен
равен
а) б)
в) г)
Неопределенный интеграл равен
а) б)
в) г)
Неопределенный интеграл
 равен
равен
а)
![]() б)
б)
![]()
в) г)
Значение предела
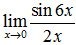 равно
равно
а) 3 б) 2 в) 6 г) 1/3
Значение предела
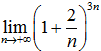 равно
равно
а) e6 б) 1 в) e2/3 г) e
Значение предела
 равно
равно
а) e б) 0 в) 1 г) ∞
Значение предела
 равно
равно
а) 1 б) -0,5 в) 0 г) ∞
Значение предела
 равно
равно
а) 2 б) 0 в) 1/2 г) 3
Значение предела
 равно
равно
а) 2 б) 0 в) не определено г) 3
Значение предела
 равно
равно
а) 1 б) -0,5 в) -1 г) ∞
Значение предела
 равно
равно
а) 2 б) 0 в) -1 г) 1
Значение предела
 равно
равно
а) 0,5 б) 2 в) 0 г) -∞
Производная функции
 равна
равна
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Производная функции
 равна
равна
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Угловой коэффициент касательной к графику функции у = x2+2x-4 в точке x0 = -1
а) 0 б) 5 в) -1 г) 2
Производная функции
 равна
равна
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Значение предела
 равно (воспользуйтесь правилом Лопиталя)
равно (воспользуйтесь правилом Лопиталя)
а) 4 б) 0 в) 1 г) 2
Значение предела
 равно
(воспользуйтесь правилом Лопиталя)
равно
(воспользуйтесь правилом Лопиталя)
а) ∞ б) e в) 0 г) 1
Интеграл
 равен
равен
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Интеграл
 равен
равен
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Значение интеграла
 равно
равно
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Выберите замену в интеграле:

а)
t
= 7-3x
б) t
= 3x
в)
![]() г) t
= (7-3х)21
г) t
= (7-3х)21
Формула для вычисления площади фигуры

а)
![]() б)
б)
![]() в)
в)
![]() г)
г) ![]()
Формула для вычисления площади фигуры
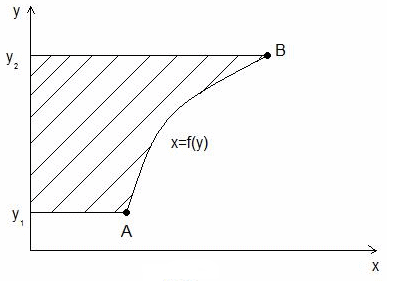
а)
б)
в)
г) ![]()
Формула для вычисления площади фигуры

а)
б)
в)
г) ![]()
Площадь фигуры, ограниченной параболами y = 4 - x2 и y = x2 - 2x

а)
9 б) ![]() в) 9,5 г) 4,5
в) 9,5 г) 4,5
