55

А втономная некоммерческая организация

высшего профессионального образования

«Алтайский институт финансового управления»

(АНО ВПО АлтИФУ)

Кафедра менеджмента, информационных технологий и бизнеса

КЕЙС-ПАКЕТ ДИСЦИПЛИНЫ

«МАТЕМАТИКА»

для студентов заочной формы обучения по направлению

«МЕНЕДЖМЕНТ»

Подготовила:

Рябыш Оксана Викторовна

Барнаул - 2013

Содержание

для студентов заочной формы обучения по направлению 1

«МЕНЕДЖМЕНТ» 1

Барнаул - 2013 1

Конспекты лекций 3

1.1. Матрицы и действия над ними 4

1.2. Определители 5

1.3. Обратная матрица 7

1.4. Ранг матрицы 7

1.5. Системы линейных уравнений 9

Задания для самостоятельного решения 14

1.1. Предел функций 15

1.2. Определение производной функции 17

1.3. Неопределенный интеграл 26

1.4. Определенный интеграл и площадь криволинейной трапеции 29

Задания для самостоятельного решения 31

Методические рекомендации по изучению дисциплины 33

«Математика» 33

Требования к уровню освоения дисциплины 34

«Математика» 34

Контрольные вопросы 35

Контрольные тестовые задания 36

!!! Методические указания 49

по выполнению контрольной работы 49

Задания для домашних контрольных работ 50

Рекомендуемая литература 54

Конспекты лекций

Основные обозначения

1. Матрицы и действия над ними

2. Определители

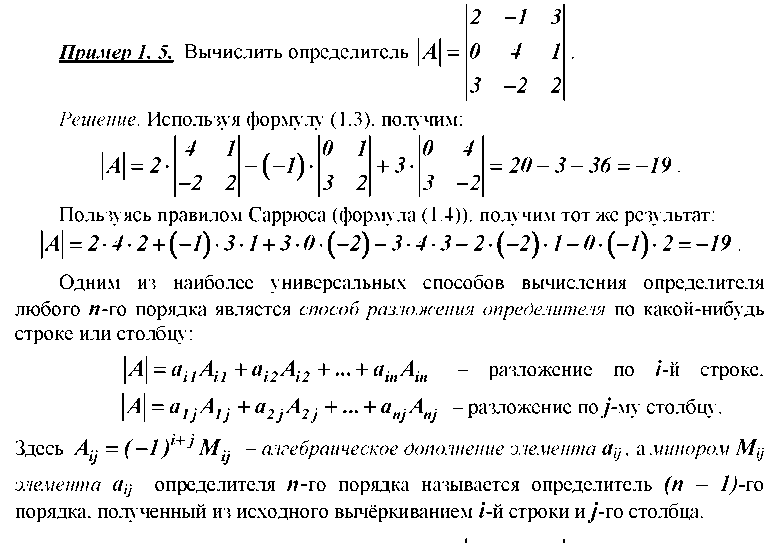
3. Обратная матрица

4. Ранг матрицы

5. Системы линейных уравнений

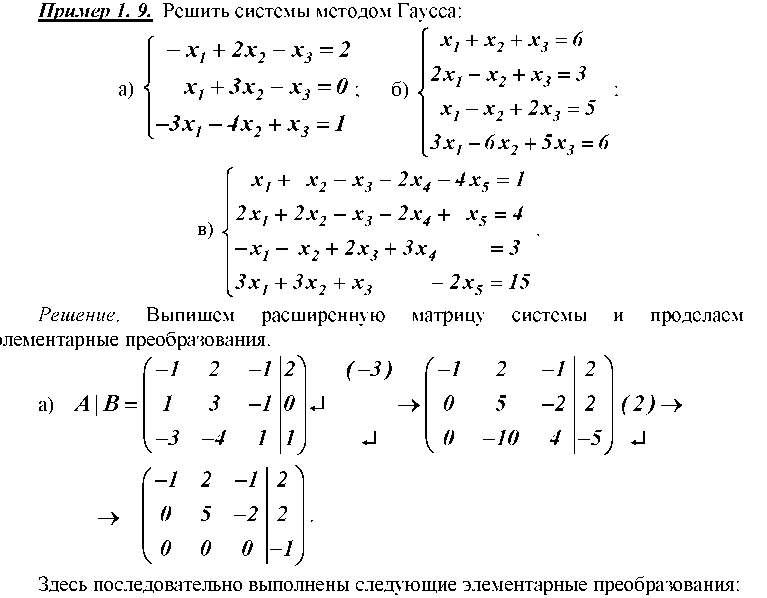
Задания для самостоятельного решения

Задание 1. Даны матрицы

Вычислите следующие матрицы :

Задание 2. Вычислите определитель 3-го порядка:

1) разложив по элементам какой-либо строки или какого-либо столбца;

2) по правилу Саррюса (по правилу «треугольника»).

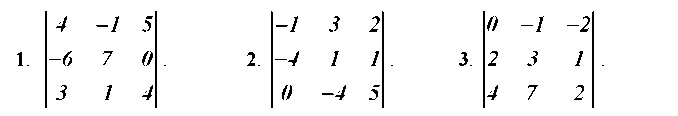
Задание 3. Даны системы трех линейных уравнений с тремя неизвестными. Решите ее:

1) с помощью правила Крамера;

2) с помощью обратной матрицы.

Сравните результаты.

Задание 4. Методом Гаусса найдите множество решений однородной системы трех линейных уравнений с четырьмя неизвестными.

1. Предел функций

Примеры:

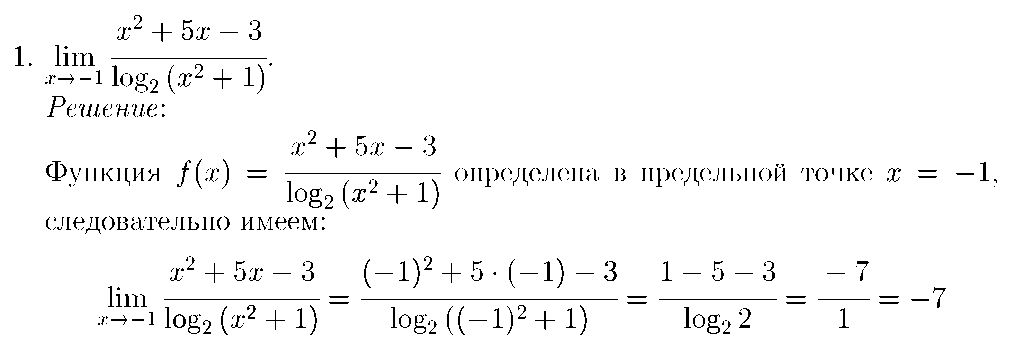
2. Определение производной функции

Логарифмическое дифференцирование

Правило Лопиталя для вычисления пределов

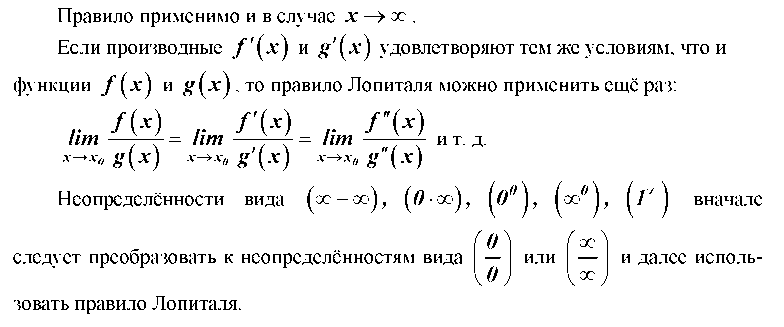
Примеры:

3. Вычислите пределы, применяя правило Лопиталя:

Приложения производной к исследованию функции

3. Неопределенный интеграл

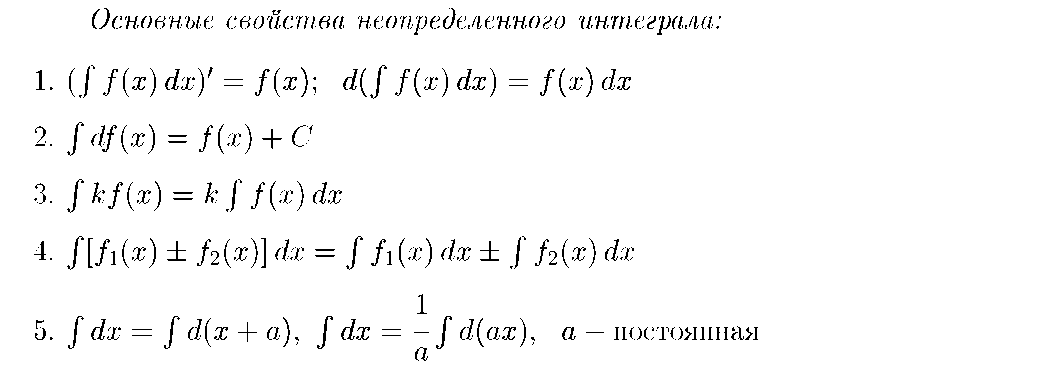
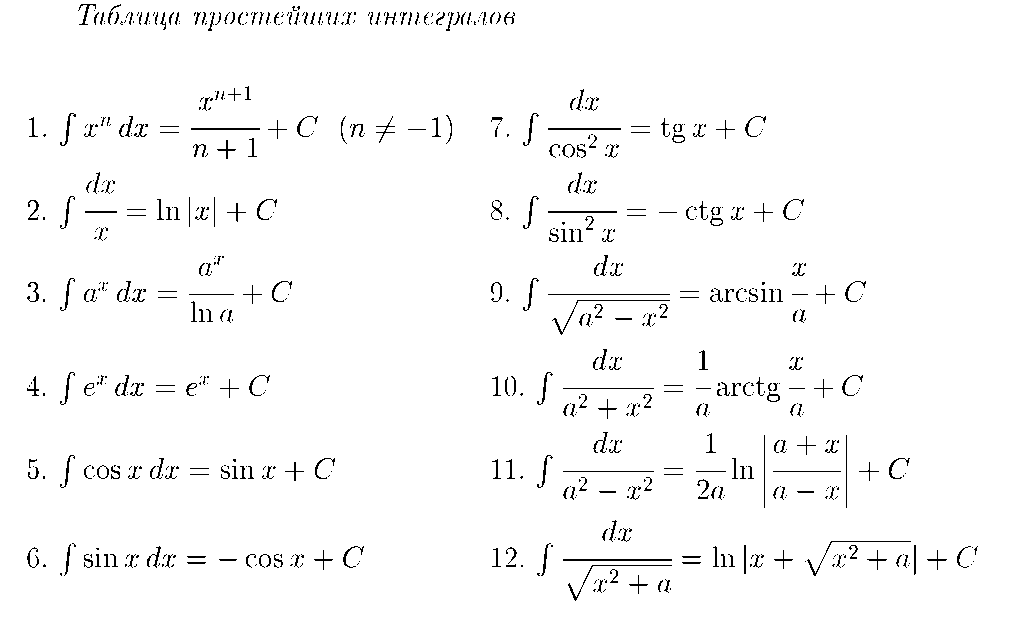
Примеры:

4. Определенный интеграл и площадь криволинейной трапеции

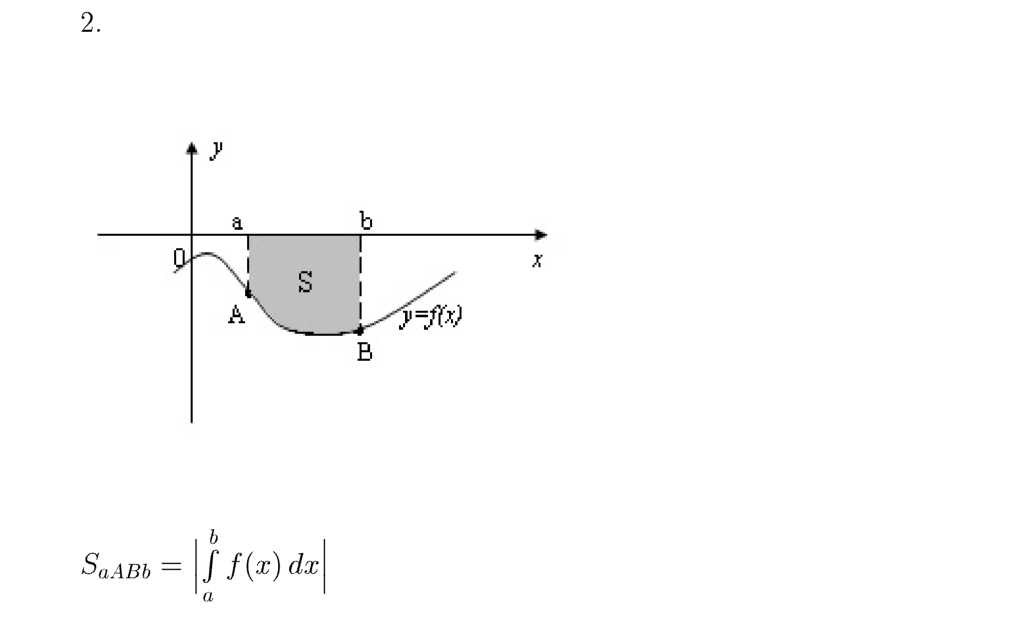
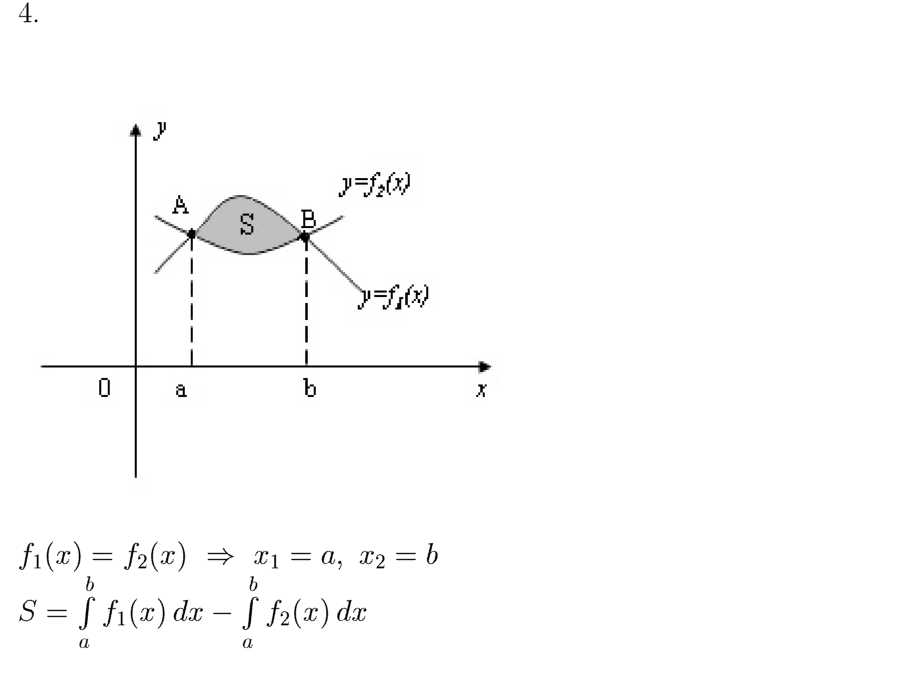
Задания для самостоятельного решения

Задание 1. Вычислите пределы:

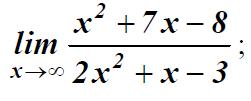
Задание 2. Найдите производные следующих функций:

Задание 3. Вычислите пределы функций с помощью правила Лопиталя:

;

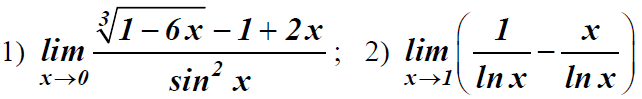3) ; 4) .

Задание 4. Исследуйте функцию и постройте ее график:

Задание 5. Найдите неопределенные интегралы:

1)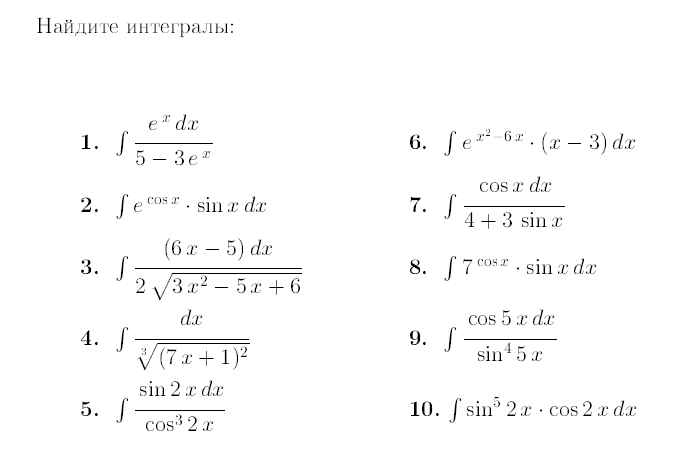 2)

3) 4)

Задание 6. Вычислите площадь криволинейной трапеции, используя определенный интеграл. Сделайте чертеж.

1) 2)

3)

Методические рекомендации по изучению дисциплины «Математика»

Для эффективного усвоения учебного материала дисциплины «Линейная алгебра» целесообразно выполнять все указания преподавателя, предусмотренные курсом.

Особое внимание следует уделять самостоятельной работе, которая заключается в следующем:

• изучение теоретического материала конспектов лекций;

• проработка решений типовых заданий, представленных в конспектах;

• чтение дополнительной учебно-методической литературы;

• подготовка ответов на вопросы отчетности по дисциплине;

• овладение умениями решать типовые задания, предложенные для самостоятельного решения;

• подготовка к экзамену.

В результате изучения данного курса каждый студент должен овладеть основными понятиями линейной алгебры; умениями решать типовые задачи курса.

Для эффективного изучения теоретической части дисциплины «Линейная алгебра» целесообразно:

• построить работу по основным этапам, соответствующим предложенным темам лекционного материала;

• проверить свои знания по контрольным вопросам к экзамену;

• изучить решения типовых заданий, предложенных в конспектах;

• выполнить задания для самостоятельного решения;

• проверить свои знания и умения, выполнив тестовые задания;

• выполнить контрольную работу!

Требования к уровню освоения дисциплины «Математика»

№ п/п	Знания, умения, навыки	Форма контроля
1.	Обучающийся будет знать:
	Раздел 1. Линейная алгебра Понятие матрицы. Виды матриц. Равенство матриц. Действия с матрицами. Транспонирование матриц. Квадратные матрицы. Определители квадратных матриц второго, третьего и n‑го порядков. Алгебраическое дополнение. Свойства определителей. Обратная матрица и алгоритм ее вычисления. Понятие минора n‑го порядка матрицы. Ранг матрицы. Вычисление Ранга матрицы с помощью элементарных преобразований. Система m линейных уравнений с n переменными (общий вид). Матрица системы. Матричная форма записи системы линейных уравнений. Совместные (определенные и неопределенные) и несовместные системы. Решение системы: а) по формулам Крамера; б) методом обратной матрицы; в) методом Гаусса. Раздел 2. Математический анализ Определение понятия предела функции. Основные теоремы, на которых основано вычисление пределов. Формулы первого и второго замечательных пределов. Теоремы о пределах (об единственности предела; о пределе суммы, произведения и частного). Определение производной функции. Геометрический смысл производной. Уравнение касательной к графику функции y = f(x) при x = x0. Механический смысл производной. Производные простейших элементарных функций. Правила дифференцирования суммы, разности, произведения и частного. Правило дифференцирования сложной функции. Смысл логарифмического дифференцирования, условия его применения. Правил Лопиталя и условия его применения для вычисления пределов. Общую схему исследования функции. Правило нахождения промежутков монотонности и отыскания экстремумов функции. Правило отыскания промежутков выпуклости и вогнутости, точек перегиба функции. Определение неопределенного интеграла. Свойства неопределенного интеграла. Формулы простейших интегралов. Основные методы интегрирования. Формула Ньютона-Лейбница. Формулы для вычисления площадей фигур с помощью определенного интеграла.	контрольная работа
2.	Обучающийся будет уметь:
	Раздел 1. Линейная алгебра Выполнять действия (сложение и вычитание матриц, умножение матрицы на число, умножение двух матриц). Находить транспонированную, обратную матрицу. Вычислять определители второго и третьего порядков. Решать систему линейных уравнений: а) по формулам Крамера; б) методом обратной матрицы; в) методом Гаусса. Раздел 2. Математический анализ Вычислять пределы, используя различные приемы раскрытии неопределенностей разного вида, теоремы, на которых основано вычисление пределов, формулы первого и второго замечательных пределов. Находить производную функции, используя таблицу производных элементарных функций, правила дифференцирования, прием логарифмического дифференцирования. Составлять уравнение касательной. Применять правило Лопиталя для вычисления пределов. Исследовать функции (находить промежутки монотонности и экстремумы функции, промежутки выпуклости и вогнутости, точек перегиба функции). Вычислять неопределенные интегралы различными методами. Применять формулу Ньютона-Лейбница для вычисления площадей фигур с помощью определенного интеграла.	контрольная работа