2. Термодинамический анализ

Цель: теоретическое обоснование возможности практической реализации выбранного способа производства, а также получение данных по предельной эффективности данного химического процесса.

3. Изобарно-изотермический потенциал (энергия Гиббса)

Направленность (самопроизвольность протекания) химических реакций определяют по значениям термодинамических потенциалов.

Наиболее подходящим потенциалом (характеристической функцией) для химических реакций, протекающих, как правило, в изотермических условиях (T=const) при постоянном давлении (p=const), является изобарно-изотермический потенциал – энергия Гиббса (ΔG). Она включает в себя два слагаемых:

• первое - ΔН связано с тепловым эффектом реакции;

• второе - ТΔS связано с изменением энтропии процесса;

Напротив, все процессы, в результате которых упорядоченность системы возрастает (конденсация, полимеризация, сжатие, уменьшение числа частиц), сопровождаются уменьшением энтропии.

Изменение стандартной энергии Гиббса в процессе химической реакции равно алгебраической сумме произведений стехиометрических коэффициентов всех участников реакции на их значения ΔG⁰ образования с учетом знаков. Для реагентов стехиометрические коэффициенты - отрицательны, для продуктов реакции – положительны.

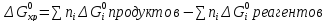
Соответственно для каждого вещества его стандартная энергия Гиббса может быть вычислена как сумма стандартного изменения энтальпии образования его из простых веществ и энтропии при 298 К с учетом температурного множителя:

Обычно по справочным данным рассчитывают изменения ΔH0 и ΔS0 реакции по формуле, аналогичной формуле энергии Гиббса:

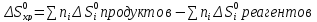
Если:

• ΔG > 0, реакция термодинамически запрещена;

• ΔG < 0, не имеет термодинамических ограничений;

Константа равновесия связана с изменением стандартного изобарно-изотермического потенциала (энергия Гиббса) реакции уравнением Вант-Гоффа:

ΔG° = ΔН° – ТΔS° = – RT lnK

Связь константы равновесия реакции и температуры (изобара Вант-Гоффа):

Это уравнение позволяет проводить термодинамический анализ реакционных систем при известных или рассчитанных по справочным данным изменениях энтальпии (ΔН°) и энтропии (ΔS°) реакции.

В соответствии с законом действия масс константа равновесия устанавливает связь между концентрациями исходных веществ и продуктов реакции, и, следовательно, определяет достижимый в данных условиях максимально возможный выход продукта.

Для реакции: аА + вВ = rR + sS

константа равновесия может быть выражена через молярные концентрации веществ – концентрационная константа (К_с):

Для газофазных реакций константу равновесия выражают через парциальные давления реагентов:

Для идеальных газов К_с и К_р связаны соотношением

Где изменение количества молей

В первом приближении можно считать, что константа равновесия не зависит от давления и является функцией только температуры. Это справедливо при низких давлениях и высоких температурах. При высоких давлениях законы для идеальных газов перестают описывать наблюдаемые зависимости. Были введены понятия летучести, активности и коэффициента активности. Взаимосвязь летучести и давления выражается уравнением:

где f_i – летучесть i-компонента (параметр вещества, характеризующий его способность переходить из жидкого состояния в газообразное) , P_i – парциальное давление i-компонента, γ_i – безразмерный коэффициент активности (индивидуален и зависит от природы газа и вещества), зависящий от давления и температуры.

Фугитивность – это такое давление реального газа, при котором газ ведет себя как идеальный.

При f→P свойства реальных газов приближаются к свойствам идеальных газов, а коэффициент фугитивности стремится к единице γ→1.

Активностью данного вещества называют отношение его летучести к той же величине, в стандартном состоянии: . За стандартное состояние газа принято его состояние при любой температуре с летучестью, равной одной атмосфере. Из этого следует, что летучесть газа совпадает с его активностью.

Выражение для константы равновесия с использованием равновесных летучестей (активностей) и коэффициентов активности выглядит следующим образом: , где К_f – истинная (термодинамическая) константа равновесия.

Истинная термодинамическая константа равновесия К_f или К_а не зависит от концентрации компонентов в системе.

Определяемые экспериментально через анализ концентраций кажущиеся (наблюдаемые) константы равновесия К_с и, соответственно, К_р зависят от концентраций реагирующих веществ или парциальных давлений и общего давления.

Константы равновесия также могут быть выражены, например, через отношения мольных долей N_i участников реакции (K_N).

Для реакций, протекающих при небольших давлениях без изменения объема: К_а = К_р =К_f = К_N.

Термодинамическая константа равновесия является функцией только температуры.

С другой стороны, кажущаяся константа равновесия (К_р) при высоких давлениях зависит от давления, поскольку меняется К_γ.

Для определения конечного состава системы используют кажущуюся константу равновесия; из расчёта на основе термодинамических параметров (изменение энтропии и энтальпии реакции) мы знаем истинную величину константы равновесия К_f или K_a в зависимости от фазового состояния веществ и температуры.