Laboratory work 3 determination of local resistances coefficients Brief theoretical information
Any device or conduit element where liquid flow changes its configuration or direction is called local resistance. Here intensive whirls arise and, being the sources of energy dissipation, is turning into heat. As a result full flow energy at the exit from local resistance is less than at the entrance.
The local resistance Losses of Pressure are determined by Veihsbah’s formula:
,
(3.1)
where
is coefficient of local resistance, depending on the type of the
resistance and the flow rate; Vav
is cross- section flow speed in the pipe, where local resistance is
located.
The resistance coefficient value is to be find from equation 3.1
.
(3.2)
From
this formula it follows that coefficient of resistance
is non-dimensional and equals the relation of the lost head to
velocity head.
Because of different pipe dimensions at local resistance entrance and exit the speeds and kinetic energies there can be different. That is why the local resistance coefficient, calculated with speed in the pipe of smaller cross-section is considerably less than the coefficient in the pipe of wider cross-section. For more convenience we compare different local resistance coefficients according to the speed in narrower cross-section, irrespective of the entrance or exit.
Usually there are a lot of local resistances in aircraft hydraulic and fuel systems: filters, faucets, valves, angles and other devices and fixtures,
having various geometrical configurations. In spite of great variety of local resistances it is possible to determine the following groups:
- smooth or sudden expansion;
- smooth or sudden narrowing;
- smooth or sharp turning.
Common resistance usually includes combination of several groups of resistances mentioned above.
It is difficult to determine coefficient of resistance theoretically due to complicated liquid flow process through local resistances. Therefore, these coefficients are determined by experiments.
The losses in local resistance are determined as difference of full specific energies at entrance and exit of local resistance:
.
(3.3)
Considering, that Z1 = Z2 and taking into account the relation of speeds V1av and V2av, of flow continuity V1S1=V2S2 , formula 3.3 can be represented by the following:
;
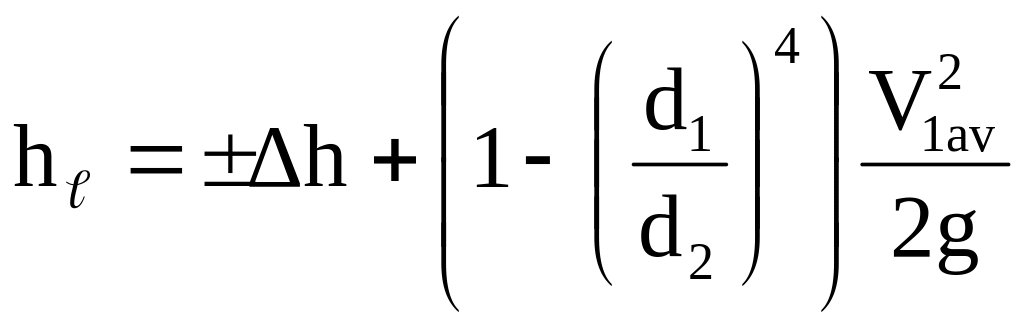(3.4)
,
(3.5)
where
is difference of specific potential energies of pressure,
and
is difference of specific kinetic energies.
With formula 3.2 and taking into account 3.4, 3.5 we can get the formulas for coefficient of local resistance:
;
(3.6)
.
(3.7)
Equation 3.6 is used when speed at entrance of local resistance V1 exceeds the speed V2 on exit. An inlet pipe diameter is less than that of outlet pipe both for sudden and smooth expansions. Equation 3.7 is used when speed at entrance of the local resistance V1 is less than speed V2 at exit, an inlet pipe has a lagger diameter than outlet both for sudden and smooth narrowing.
If inlet and outlet pipes are equal in size, the equation of coefficient of local resistance is simplified and determined by formula 3.2.
Flow
of liquid through local resistance can be both laminar and turbulent
depending on speed and liquid viscosity (temperature). The
coefficients
of
the resistance should be considered as functions of Re-number.
The loss of head due to an obstruction in a pipe may be looked upon as due to the sudden enlargement beyond the obstruction.
This phenomenon is made use of in an instrument known as a pipe orifice which is used for measuring the flow of liquid. The orifice forms an obstruction in the pipe and the loss of head is measured by means of pressure gouges.
Usually
in aircraft fuel
pipes Re numbers are considerably
higher than in hydraulic pipes.
Taking into account that the resistance coefficient
with large Re numbers do not depend on Re numbers it is possible
that one can use an auto model dependence for the values of
coefficients
of
common hydraulic units and elements to calculate fuel aircraft
systems:
flexible
pipe resistance -
=
0,3; standard 900
(drilled)
=
1,2...1,3; branch tap
=
3,5; fuel faucet
=
1,0.. - 2,5; reverse valve
=
2,0; filter reticulated
=
1,5...2,5; sensor of flow meter with rotating impeller
=7,0,
sensor of flow meter with locked impeller
=
11,0...- 12,0; pipe inlet (from a tank)
=
0,5...1,0; pipe outlet (in a tank)
-
1,0.
The curves of dependence of coefficient on Re- number for the most typical local resistances of aircraft hydraulic systems, received from experimental researches in the Moscow Aircraft Institute, are shown in logarithmic co-ordinates in fig. 3.1. .
Fig.3.1.Graph
of dependence of
of aircraft devices on Re-number: 1 is a felt filter; 2 is a reverse
valve; 3 is a sectional valve; 4 is a tripping
faucet;
5 is a 900
angle.
The method of determining the local resistance coefficients is similar to that of determining the pipe-line resistance coefficients (Fig. 3.2).
It includes a feeding tank 1 and a calibrated tank 6 and local resistances 2, 3, 6 and 7. Faucets 4 and 5 are used for liquid speed regulating in local resistances; piezometers 8 are used for pressure measuring.
Fig.3.2.
Principle installation scheme for determining the local resistance
coefficients