4. Гидравлические и пневматические корректирующие устройства

В системах автоматического управления в качестве элементов гибких обратных связей применяет гидравлические и пневматические устройства.

Простейшим гидравлическим корректирующим устройством может служить изодром, схема которого представлена на рис. 16, а его включение — на рис. 17

Перемещение тока I и поршня 3 является входной величиной X_n, а перемещение цилиндра — выходной величиной X_ц. При перемещении поршня масло начинает перетекать через трубку 6 с калиброванным отверстием 7. Одновременно происходит вжатие пружины за счет разности перемещения цилиндра и поршня. Черев рычаг 5 перемещение передается выходному исполнительному устройству.

Обозначим силу сжатия пружины

F_пр = K_пр X_ц (83)

где К — коэффициент жесткости пружины.

Результирующее перемещение

X = X_пр – X_ц (84)

Сила трения поршня определяется зависимостью

(85)

где B — коэффициент жидкостного трения.

Сила трения уравновешивается силой сжатия пружины, т.е.

F_тр = F_пр

Тогда соотношения (83), (85) запишутся в виде

(86)

Определим перемещение цилиндра

Следовательно,

или

Введя обозначения

получим

Данное уравнение показывает, что иэодром является интегродифференцирующим элементом (дифференцирующим входной сигнал на низких частотах и интегрирующим — на высоких частотах ).

Для схемы, показанной на рис. 16, расход масла в цилиндре изодрома будет

а в поршне

где К — коэффициент пропорциональности; К_н — жесткость пружины изодрома; F_п — площадь поршня изодрома.

Сумма расходов масла Q₂ + Q₃ =Q₁

а расход масла равен Q₁ = l₁ y — l₂ x_n

Уравнение серводвигателя имеет вид

где F_n — площадь поршня серводвигателя.

Из полученных выражений можно записать дифференциальное уравнение

Или. после замены

5. Составление уравнений статики систем автоматического управления

Рассмотрим установившийся режим в системе управления синхронным генератором (рис. 18).

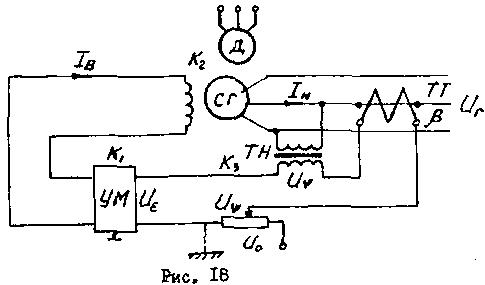
СГ — синхронный генератор; Д - двигатель; ТН - трансформатор напряжения с коэффициентом передачи К_з; ТТ - трансформатор тока с коэффициентом передачи l; УМ - усилитель мощности с коэффициентом передачи К₁; U_ — напряжение задания; U_ — напряжение на выходе ТН; пропорциональное регулируемой величине, т.е. напряжение на зажимах синхронного генератора: U_r; U_x — напряжение на выходе ТТ, пропорциональное возмущающему воздействию, т.е. току нагрузки I_н синхронного генератора; U_ — суммарное напряжение на входе усилителя мощности, определяющее закон управления в системе; I_b — ток возбуждения генератора.

Составим уравнение статики для каждого элемента системы

U_r=k₂I_B - I_H

U = U_ - U_ +U_f (89)

U_ = k_sU_r

I_B=k₁U_

U_f=lI_H

Решив систему относительно U_r, U_, I_н получим

Обозначим

=U_xx

Тогда U_r=U_xx - I_н (90)

Где U_xx — напряжение холостого хода генератора;  — коэффициент статизма системы.

Как видно из (90) выходная величина изменяется при изменении нагрузки по линейному закону (рис. 19)

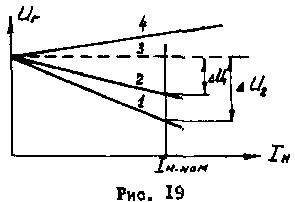
Рассмотрим несколько случаев:

1. l =0, тогда

В отсутствии системы управления уравнение генератора будет иметь вид

U_r =U_xx - I_н (91)

что соответствует кривой 1 на рис. 19. При номинальном токе нагрузки I_{н ном}, согласно (91) наблюдается падение напряжения на величину

U_r1=L

При включении системы управления (90)

что соответствует кривой 2 на рис. 19.

Найдем отношение

(92)

Уравнение (92) показывает, что статизм нагрузочной характеристики при наличии системы управления уменьшается в (1+к) раз.

Статизмом характеристики называют величину

Степень точности С системы определяется выражением

C=1+k

Коли задана допустимая величина изменения выходной величины, т.е. задан статизм характеристики, то из (92) можно определить величину К. Зная коэффициенты передачи объекта управления К₂ и измерительных устройств К₃, можно рассчитать требуемую крутизну характеристики усилителя К_1.

2. l>0. Из (90) видно, что для того, чтобы напряжение U_r не зависило от тока нагрузки I_н необходимо повышать коэффициент К₁ до бесконечности, что принципиально невозможно, либо применять компаундирующую связь по току нагрузки (цепь трансформатора тока).

Если выбрать l=/К₁К₂, то  будет равно нулю и входная величина не будет зависеть от возмущающего воздействия (линия 3 на рис. 19).

При l>/K₁K₂ получим систему с положительным статизмом, т.е. с перекомпенсацией (линия 4 на рис. 19).

Другой путь сделать регулируемую величину независимой от возмущения, это применение астатических систем.

Преобразуем рассматриваемую систему в астатическую (рис. 20).

Составим уравнения для отдельных элементов системы:

U_r=k₂I_B - I_H

U = U_ - U_

U_ = k_sU_r

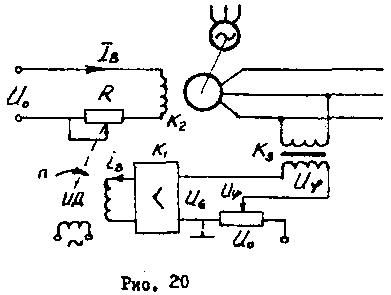
Из схемы следует, что скорость изменения тока возбуждения I_B будет пропорциональна скорости вращения  исполнительного двигателя ИД, т.е.

При возникновении ошибки управления U_ в обмотке управления двигателем ИД будет протекать ток i_В и двигатель начнет вращаться, передавая движение через редуктор на движок сопротивления R. Это повлечет за собой увеличение тока возбуждения I_b и, следовательно, U_r. Двигатель будит стоять, если U_=0, а это возможно лишь при условии: U_=U_ т.е. регулируемая величина соответствует заданию.