2.3.Гибкие обратные связи
Как известно, передаточная функция для реального дифференцирующих звена равна.
W(S)=KST
Однако
для реальных дифференцирующих цепей,
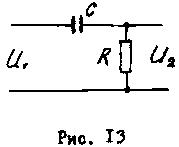
таких, например, как RS
цепи (рис.13) передаточная функция имеет
вид
где T=RC
Учитывая, что S =j имеем
и при условии, что js<<1 можно принять, что приближенная передаточная функция в области относительно малых значений , удовлетворяет условию W(S)=ST
Рассмотрим влияние гибких обратных связей на изменение параметров звеньев прямой цепи. Примем передаточную функцию гибкой обратной связи ГОС равной Woc(S)=KocST
Пусть
в прямой цепи стоит апериодическое
звено с передаточной функцией
Тогда
т.е. эквивалентная передаточная функция имеет коэффициент передачи равный исходной, а эквивалентная постоянная времени увеличивается.
Таким образом, гибкая обратная связь делает апериодическое звено более инерционным.
Пусть
теперь в прямой цепи находятся два
апериодических звена, т.е.
а ГОС Woc(S)=KocST
При этом
где К= К1К2, а значения эквивалентных постоянных времени Т11 и Т21 определяются из уравнении
Т11 Т21 = Т1 Т2
Т11 + Т21 = Т1 + Т2 +К1 К2 Кс Т
Из этого следует, что значение одной из эквивалентных постоянных времени становится больше большей из двух исходных, значение второй — меньше меньшей исходной постоянной времени, т.е.
Т11 > Т1; Т21 < Т2
( при этом предполагается, что Т1> Т2 ).
Если же коэффициент передачи объекта К=К1К2 стремится к бесконечности, то
т.е. передаточная функция становится равнозначной интегрирующему звену и объект приобретает астатические свойства.
Однако,
в действительности
Следовательно,
при
т.е.
объект, охваченный обратной связью будет вести себя как система, реагирующая на отклонение и его интеграл, и, следовательно, также будет иметь астатические характеристики. Такую систему, реагирующую на отклонение и его интеграл, обычно называют изодромной.
3. Электрические корректирущие цепи
Электрические корректирующие устройства получили наиболее широкое распространение, ввиду простоты их реализации. Линейные корректирующие устройства выполняет операции дифференцирования, интегрирования или их сочетание, например, операции интегрирования на одних частотах и операции дифференцирования на других частотах.
Рассмотрим расчет некоторых простейших корректирующих цепей, составленных из резисторов и емкостей.
Составим дифференциальное уравнение для схемы, показанной на рис. 14
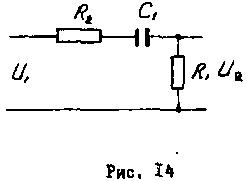
На входе цепи действует напряжение U1, требуется найти дифференциальное уравнение, связывавшее напряжение на выходе и на входе звена, и передаточную функцию.
По цепи, составленной из R2C1 и R1, протекает ток i. Тогда
Разрешим данную систему, относительно интересующих нас величин, т.е. U2 и U1, путем исключения из системы промежуточных переменных, т.е. тока i=U2/U1. Для упрощения учтем оперативное изображение интеграла. При этом
Обозначим R1C1=T1; R2C1=T2. Тогда (T1+T2)pU2+U2=T1pU
При
переходе к оперативному преобразование
Лапласа при нулевых начальных условиях
получим передаточную функцию
Определим передаточную функцию сложного корректирующего устройства с учетом сопротивления нагрузки (рис. 15).
Примем следующие значения параметров
R1=2ком ; C1=20мкф; Rн=1ком;
R2=1ком; C2=5мкфж
Составим систему уравнений
U1=R1I1+R2i+RнI2
По закону Кирхгофа
i1+ic1=i2+Ic2=i
Найдём ic1 и Ic2
Ic1=R1C1Pi1
Ic2=R3C2Pi2
Тогда i2=R3C2Pi2=i1+ R1C1Pi1
(1+ R3C2P)i2 = (1+ R1C1P)i1
Откуда
Следовательно
Или
Где T1=R1C1 T2=RHC2
Где
Условные вещественности корней знаменателя, т.е. >=1, будет
[(R1+R2)T2+(R1+R2)T2]2 >.4T1T2R2(R1+R2+RH)
или после преобразований
[T1 (R2+R3) - T2 (R1+R2)]2 —.4T1T2R1R3 >0
Следовательно
уравнение ( ) можно представить в виде
Где
Проведём численное решение
K=1/(2+1+1)=0,25
T1 =40*10-3=0,04 T2=5*10-3=0,005 сек
Определим корни знаменателя по формуле (82)
1/(2+1+1)0,04*0,005p2+[((1+1)0,04+(2+1)0,005)/(2+1+1)](p+1)=0
0.00005p2+0.02375p+1=0
p2+475p+20000=0
p1= -47 p2= -428
T1’= - 1/p= - 1/ -47=0.0213c T2’= - 1/p2= - 1/428=0.00233
Следовательно, передаточная функция
