2. Изменение параметров звеньев при помощи обратных связей

При разработке САУ обычно не удается выполнить систему так, чтобы она будучи составлена из основных звеньев работала устойчиво и удовлетворяла заданным при проектирования показателям качества. В большинстве случаев приходится изменять параметры некоторых основных звеньев путем введения жестких или гибких обратных связей, путем введения различных корректирующих устройств,

Существует различные методы коррекции систем. Основное значение и наиболее широкое распространение приобрели дополнительные, внутренние обратные связи. Системы управления, имеющие внутренние и главные обратные связи, называются многоконтурными.

Известно, что охват звена обратной связью приводит к изменению передаточной функции W(S). При этом эквивалентная передаточная функция принимает вид

Если в цепь обратной связи поступает сам выходной сигнал звена, т.е. W_oc(S)=K_oc, то такая обратная связь называется жесткой обратной связью.

Гибкой обратной связью называется связь, при которой сигнал обратной связи пропорционален производной выходного сигнала звена. Гибкие обратные связи отличаются тем, что они действуют в переходных режимах и не оказывают влияния в остановившемся состоянии.

2.1. Введение жестких обратных связей

Рассмотрим инерционное звено, охваченное жесткой обратной связью ЖОС, рис.12

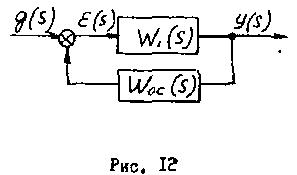
т.е. эквивалентное звено получается также инерционным, но при измененных коэффициенте усиления и постоянной времени. При отрицательной обратной связи происходит уменьшение чувствительности звена (К_экв<К₁) и увеличение быстродействия (Т_экв<T₁).

При положительной обратной связи эквивалентная передаточная функция равна

где

При К_осК₁<1 эквивалентное звено является инерционным звеном, при этом К_экв>К₁, Т_в>Т₁, что приводит к уменьшению быстродействия звена, так как мерой инерционности является постоянные времени.

При К_осК₁>1 эквивалентное звено становится неустойчивым и является неминимально-фазовым звеном.

Cледует отметить, что не всегда удается реализовать идеальные жесткие обратные связи. Реально жесткая обратная связь может иметь постоянную времени T_с, например, если для получения жесткой обратной связи используется обмотка возбуждения электрических машин, обладающая значительной индуктивностью. В этом случае, цепь обратной связи представляется апериодическим звеном с передаточной функцией

тогда

(80)

где

При такой обратной связи эквивалентное звено становится звеном второго порядка. При соответствующем выборе параметров (S>1) цепи обратной связи выражение (80) можно записать в виде

где

Следовательно, для реализация ЖОС требуется выбирать устройства с малыми Т_с, так как с увеличением Т_с влияние отрицательной обратной связи будет уменьшаться ввиду того, что Т_с входит в числитель и компенсирует влияние слагаемого входящего в знаменатель.

Особенно эффективно применение жестких обратных связей для стабилизации нейтральных объектов управления.

Рассмотрим интегрирующее звено с передаточной функцией

охваченное ЖОС W_oc(S)=K_oc

При этом

или

где

Таким образом, интегрирующее звено, охваченное жесткой обратной связью, превращается в инерционное звено с положительным самовыравниванием.

Если ЖОС не идеальная, т.е.

то

где

Для получения не колебательных переходных процессов необходимо, чтобы выполнялось соотношение

2.2 Применение неединичных жестких обратных связей для устранения статических ошибок

Пусть

В этом случае

(81)

Для того чтобы сигнал y(t) воспроизводился без ошибки. необходимо обеспечить условие W_з(S)=1. При этом должно выполняться условие

1+W_oc(S)W(S) – W(S)=0

Откуда

W_oc(S)W(S)=W(S) – 1

Так как порядок полинома А(S) больше порядка полинома B(S), то после разложения в степенной ряд получим

W_oc(S)=k_oc – (T_oc1S+T_oc2S²+…)

Пусть

Тогда

Условию отсутствия статической ошибки соответствует равенство свободных членов числителя и знаменателя в выражении (81), т.е. из условия W_з(0)=1 имеем

K₁=1+mK₁

Следовательно

Откуда эквивалентная передаточная функция разомкнутого эквивалентного звена принимает вид

что эквивалентно астатизму первого порядка.