Методические указания по выполнению практических занятий по курсу «теория автоматического управления (линейные cap)»

ВВЕДЕНИЕ

.Современная промышленность и сельское хозяйство характе­ризуется непрерывным увеличением производительности машин и агрегатов, повышением качества выпускаемой продукции. Для управления различными процессами во всех областях техники при­меняется системы автоматического управления.

Система автоматического управления - замкнутая динамиче­ская система направленного действия, обеспечивающая определенную функциональную связь между регулируемыми и задающими воздействиями посредством управлявших воздействий, между управляющей и управляемой подсистемой, между регулятором и объектом управ­ления.

Эта функциональная связь может быть получена в виде алгеб­раических, дифференциальных и интегральных уравнений, которые образуют математическую модель физической системы или отдельно­го ее элемента.

Перед разработкой математических моделей физических процессов необходимо четко сформулировать цель и задачи управления, так как модели одного и того же физического процесса могут иметь мало общего, если они разрабатывались для разных целей.

Для разработки моделей физических процессов необходимо определить:

• область действия или границы изучаемого процесса;

• глубину детализации;

• физические ограничения на переменные состояния;

• характер управления: управление в установившемся режиме и управление динамическое;

• требуемую точность;

• величины переменных состояния, известные переменные управле­ния;

• оценить возмущающие воздействия и другие неуправляемые пе­ременные.

Часто для простоты описания вводятся различные упрощающие предположения, видное место могут занимать интуиция и здравый смысл. Интуиция играет важную роль при формировании основных допущений в установлении основных зависимостей между ключевыми переменными, а также при выработке первоначального подхода к построению модели физического процесса. Здравый смысл требует­ся для обеспечения равновесия между точностью и полнотой описа­ния модели, с одной стороны, и сложность» управления, о другой».

Базой для разработки модели физического процесса являются основные законы физики и химии, действующих в пневматических, гидравлических, тепловых, механических, электрических и ядер­ных системах,

Однако для трактовки основных законов можно применить еди­ный подход, который позволяет исследователи переходить от одной области к другой, например, от гидравлики к электротехнике; от теплотехники к механике и т.д.

Для этой же цели вводятся понятия и определения из области теории систем: элемент, соединение, система, обратная связь.

Элемент - это физический предмет, устройство, характери­стики которого можно определить на основе измерений в двух точ­ках пространства, b теории автоматического управления научают­ся, как правило, однонаправленные элементы, преобразующие вход­ные переменные в выходные.

Соединение - это точка, к которой присоединены один или более элементов. Это некоторые абстрактные точки, в которых не происходит никакого накопления, передачи, преобразования или рассеивания энергии.

Система - это совокупность элементов, в которой алгебраи­ческая сумма' энергии равна нулю, т.е. создаваемая системой энергия равна преобразуемой или рассеиваемой.

Важную роль в теории систем имеет проблема обратной связи, которую можно сформулировать следующим образом:

1. Существует некоторая цель (задача ) или, в более общем случае, совокупность задач. Предполагается, что эти задачи допускают математическую формулировку с помощью некоторых пере­менных X_1,X₂…X_n , совокупность которых обозначена через R. .

2. Для выполнения этих задач необходима определенная физи­ческая реализация, т.е. аппаратура. Эта аппаратура образует управляемый объект со входами U₁, U₂, U_m, совокупность которых обозначена через М. Очевидно, непосредственное решение проблемы состоит в том, чтобы поместить между R.и М устройство, которое переводило бы поставленные задачи на язык сигналов, соответствующих характеру объекта.

3. Применение управляющего устройства УУ могло бы решить проблему, если бы не было некоторых препятствий, возникающих весьма часто и заключавшихся в неполном знании свойств объекта и неконтролируемых воздействий приложенных к объекту управления. Эти виды препятствий объединяются одним понятием «незнание». Если бы характеристики изменений во времени возмущающих воздей­ствий ₁ ₂ … _r параметров объекта a₁ a₂ … a_k были бы из­вестны, их влияние можно было бы скомпенсировать правильным выбором управляющих воздействий.

Поскольку же мы не знаем полностью, каковы изменения пара­метров и возмущающих воздействий, цель оказывается недостижи­мой.

4. Проблема также состоит в том, чтобы с заданной точно­стью выполнить поставленные задачи при помощи заданного управ­ляемого объекта, несмотря на неполноту сведений о системе.

Заданная точность может выражаться допустимой погрешностью , а «незнание» может быть таким, что даже в спроектируемой наилучшим образом разомкнутой системе максимальная результирующая погрешность будет равна m, где m>1. Для достижения поставленной цели необходимо выработать дополнительные управления U₁ U_{2 …} U_m которые вырабатываются на осно­ве сопоставления заданных и фактических значений управляемых величин. Эти сопоставления происходят в сравнивающих элементах, которые выполняют сравнение выходных величин с заданными:

 = g - KX

где К - коэффициент преобразования переменных состояния к физическим единицам измерения воздействия.

Тогда дополнительные управления U являются функциями U(,t) и вместе с основными управлениями формируют закон управления системой ( Рис. 1 ) [4] :

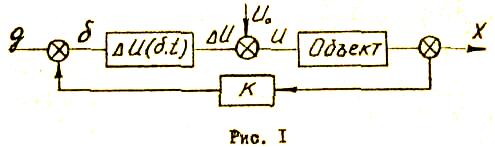
Проектирование систем автоматического управления целесообразно начинать с составления функциональной структурной схемы и затем ухе переходят к выбору и расчету параметров отдельных элементов, При выборе элементов необходимо исходить из требований, предъявляемых к системе, учитывая при этом ее назначение, надежность, экономичность, вид источника питания, внешние условия работы. Выбранные элементы должны быть согласованы по входным и выходным характеристикам.

Подавляющее большинство реальных элементов имеет нелинейные характеристики и поэтому, для таких элементов их математические модели будут описываться нелинейными уравнениями. Однако значительная часть нелинейных уравнений может быть подвергнута операции линеаризации относительно рабочей точки А₁. Такая линеаризация приводит к уравнениям в отклонения вида

X = K_^gc

где K_^ - коэффициент линеаризации K_^ = _g=A

Такая линеаризация приводит к линейным уравнениям и, в конечном итоге, к линейным математическим моделям, для которых математический аппарат анализа разработан наиболее полно.

Математическую модель, образ элемента мы будем называть звеном. В результате анализа таких моделей могут быть получены различные динамические характеристики, зависящие от времени и параметров системы [4].

Применяя преобразование Лапласа к линейным, дифференциальным уравнения при нулевых начальных условиях, получим передаточные функции звеньев и систем автоматического управления.