5.8.5. Полосовой фильтр

Рассмотри выражени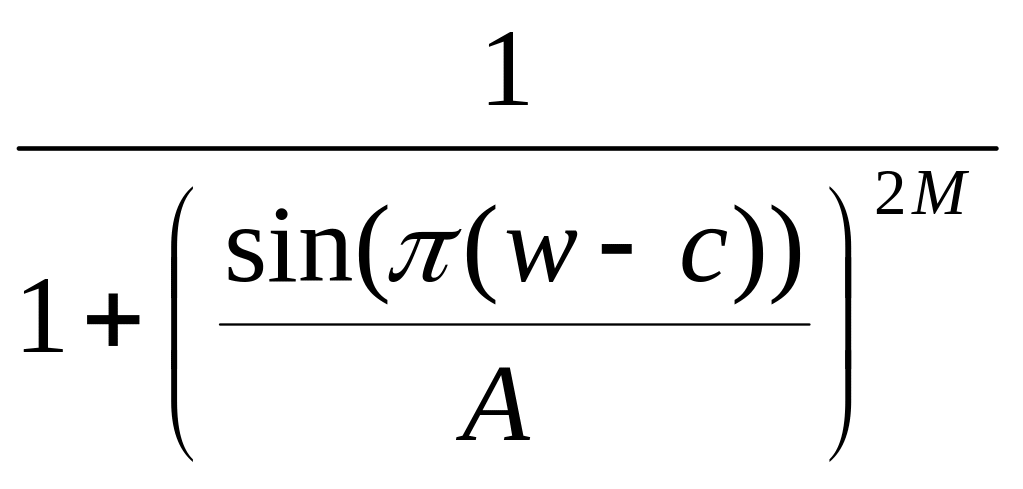е , где . Очевидно, что эта функция достигает своего максимума при . Это означает, что передаточная функция изображает полосовой фильтр. При замене в выражении получим фильтр с комплексными коэффициентами. Формально - это решение задачи, однако использование комплексного фильтра для фильтрации вещественного сигнала не очень удобно. Поэтому используют выражение вида 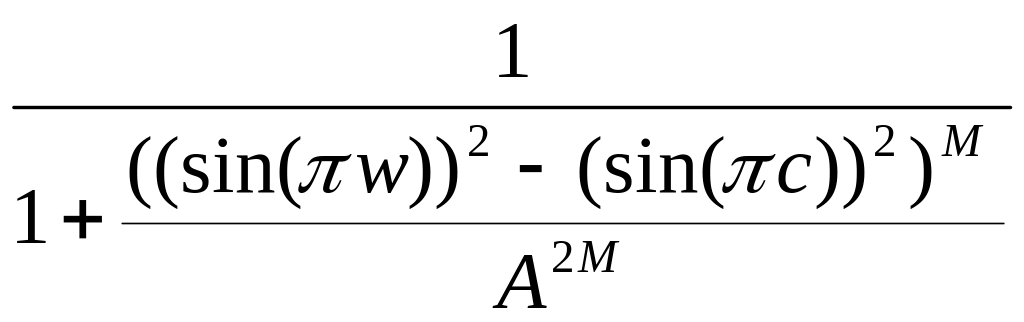. Для четного . Оно снова достигает максимума при . Используя ту же технику, что и в предыдущем случае, после замены снова сведем задачу к отысканию корней квадратного уравнения.

При последовательном соединении фильтров высоких и низких частот их передаточные функции перемножаются. В результате получаем передаточную функцию полосового фильтра. Это наиболее простой способ получения полосового фильтра, но при этом повышается размерность.

5.8.7. Фильтр скользящего среднего

Фильтр скользящего среднего получается, если в выражении для обобщенного фильтра

y[n]=- a₁ y[n-1] -a₂ y[n-2] -.. -a_k y[n-k]+

+b₀ x[n]+.. +b_mx[n-m]

где у[n]=- — отфильтрованный выход, а x[n] – вход. Если все коэффициенты а_k равны нулю, то такой фильтр называется фильтром скользящего среднего с конечной импульсной характеристики. Если необходимо простое усреднение, то все весовые коэффициенты b_i равны и дают в сумме единицу. Например, фильтр скользящего среднего с пятью входными отсчетами имеет вид

y[n]= 1/5.(y[n] + ...+y[n-4]

Этот метод имеет определенные ограничения. При использовании одинаковых коэффициентов фильтр может быть излишне инертным и недостаточно быстро реагировать на реальные изменения во входном сигнале. С другой стороны, если коэффициенты различны и убывают для больших значений индекса, то это затрудняет анализ свойств фильтра.

5.8.8. Экспоненциальный фильтр

Это авторегрессионый фильтр скользящего среднего первого порядка, определяемый следующим уравнением

y [n] = α. y[n-1] + (1- α) x[n]

Отфильтрованное значение y [n] вычисляется суммированием предыдущего значения отфильтрованного сигнала y[n-1] и последнего значения x[n] измеренного сигнала с весовыми коэффициентами. Коэффициент α лежит в интервале между 0 и 1. Уравнение можно переписать в виде

y [n] = y[n-1] + (1- α)∙( x[n]- y[n- 1])

т. е. экспоненциальный фильтр уточняет отфильтрованное значение на выходе сразу как только на вход поступает новое значение.

Вопросы для самопроверки

1. Приведите выражение алгоритма цифрового фильтра первого порядка

2. Почему не может быть реализован идеальный фильтр первого порядка?

3. Приведите методику расчета цифрового фильтра.

4. Дайте характеристику фильтрам типа скользящего среднего

5. Какие характерные особенности экспоненциального фильтра?

5.9. Основы цифровой обработки измеренной информации

5.9.1 Основные положения

Преобразованные в цифровую форму измерительные данные должны быть подвергнуты проверке. После АЦ-преобразования необходимо выполнить следующие операции — первичную обработку:

- компенсировать дрейф;

- сохранить исходные данные;

- проверить соответствие исходных данных параметрам датчика — диапазону Допустимых выходных значений и диапазону скоростей изменения выходного сигнала; если значение выходит из этих диапазонов, то должны генерировать аварийные сообщения или другие указания для оператора;

- вычислить среднее значение исходных данных ("посторонние" значения, которые заметно отличаются от других, возможно, должны быть отброшены);

- применить цифровую фильтрацию;

- сохранить отфильтрованные данные.

После цифровой фильтрации выполняются:

- пересчет единиц измерения — масштабирование (при необходимости);

- линеаризация;

- другие типы обработки данных, например статистический анализ;

- в автоматических системах — анализ входных данных для принятия решен? о дальнейших действиях, например генерации управляющих или опорных сигналов.