Вопросы для самопроверки

1. Зачем использовать аналоговый фильтр, если в системе предполагается далее цифровая обработка данных?

2. Основные свойства фильтров низких частот?

3. Чем отличается фильтр Баттерворта от активного двухзвенного фильтра низких частот?

5.6. Общая структура цифровых фильтров

Цифровая фильтрация обладает большой гибкостью, поскольку характеристики фильтра можно изменить, просто задав новые параметры соответствующей ему программы. В отличие от аналоговых, цифровые фильтры хорошо работают с длительными постоянными сигналами.

5.6.1. Основные понятия

Известно, что в АИС реакция на любую последовательность получается с помощью свертки этой последовательности и последовательности, называемой импульсной реакцией, или функцией отклика

(5.6.1)

Предположим, что входная последовательность обладает свойством: . Пусть

,

, (5.6.2)

где - натуральное, а - любые целые числа. Эта система будет физически реализуемой, если . Последовательность, заданная соотношениями (5.6.2) называется рекуррентной, или последовательностью с бесконечным временем отклика.

Пусть имеется АИС с функция отклика , на вход которой подается , а на выходе получается последовательность . Переходя в (5.6.1) к преобразованиям Фурье, получим

(5.6.3).

Функция называется передаточной функцией фильтра. Если выборка велась с частотой , то будет периодической функцией с периодом . Если последовательность - вещественная, то . Отсюда следует, функция является симметричной. В этой связи эту функцию рассматривают лишь на интервале и изображают модуль, так как он определяет коэффициент усиления на каждой из частот.

5.6.2. Фильтры с конечным временем отклика.

Предположим, что в последовательности лишь конечное число элементов отличны от нуля. В этом случае фильтр называется фильтром с конечным временем отклика

. (5.6.4)

Переходя к преобразованиям Фурье и учитывая, что , получим, что . Другими словами, передаточная функция фильтра имеет вид

(5.6.5)

5.6.3. Фильтры с бесконечным временем отклика

Фильтром с бесконечным временем отклика называется фильтр, определенный с помощью рекуррентного соотношения (5.6.2). Он может быть задан с помощью функции отклика . Последняя будет иметь бесконечное число ненулевых элементов, хотя и не может быть произвольной сходящейся последовательностью. Передаточную функцию находим, переходя в (5.6.2) к преобразованиям Фурье.

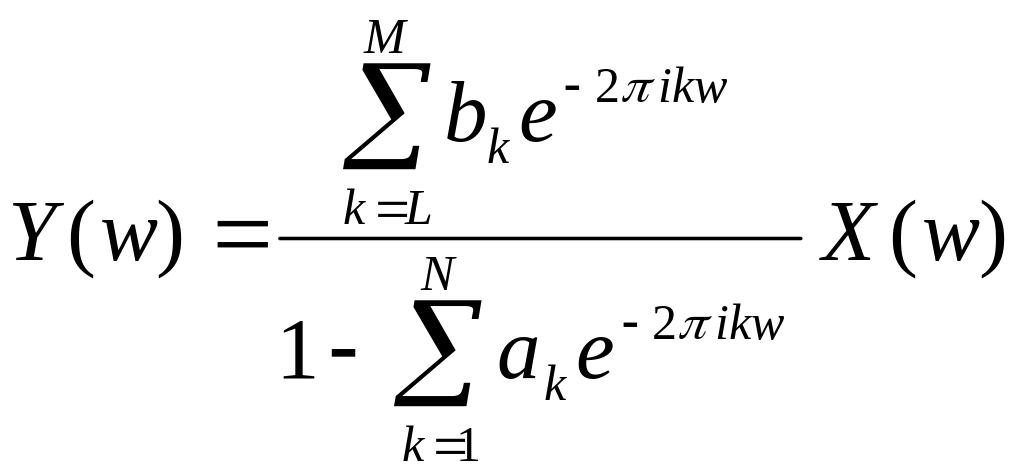(5.6.6)

Функцию отклика фильтр можно найти формальным представлением в виде ряда: где , с последующим суммированием коэффициентов при одинаковых степенях .

Вопросы для самопроверки

1. Дайте общую характеристику цифровым фильтрам.

2. Зачем предлагают использовать в системах цифровой обработки информации сигнальные процессоры вместо обычных?

3. Что такое фильтр с конечной длительностью?

4. Что такое нерекурсивный фильтр?

5.7. Фильтры первого порядка

Вместо преобразования Фурье используют также D и Z-преобразование, которые были рассмотрены выше. Известно, что

Для фильтра с бесконечным временем отклика

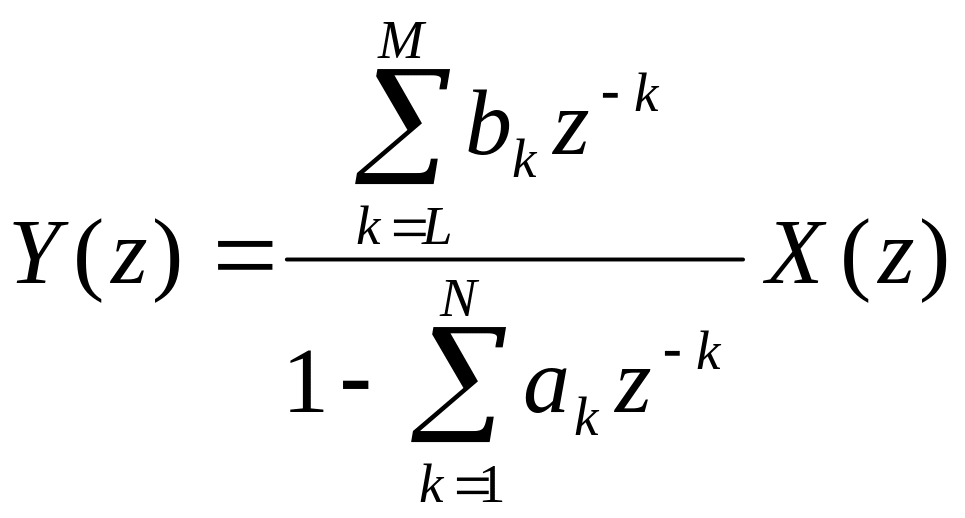(5.6.7)

Предполагается , что ряд для имеет лишь конечное число ненулевых коэффициентов при положительных степенях. В этом случае мы можем в явной форме получить члены выходной последовательности.

Идеальный фильтр. Под идеальным фильтром понимается фильтр, у которого передаточная функция имеет прямоугольную форму. Можно показать, что такой фильтр не является физически реализуемым.

Фильтр первого порядка. Рассмотрим фильтр вида

Это общий вид фильтра первого порядка. Его передаточная функция имеет вид

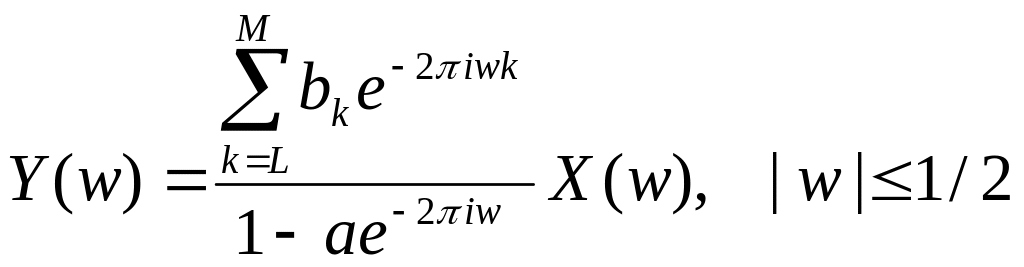(5.6.8)

Переходя к Z -преобразованию видим, что устойчивость фильтра сводится к сходимости ряда при z=1, которая имеет место тогда и только тогда, когда . В простейшем случае при передаточная функция фильтра принимает вид . В зависимости от знака график модуля имеет вид фильтра низких или высоких частот. (Фильтр низких частот пропускает низкие частоты).