3.5.1. Включение дополнительного резистора в цепь якоря.

Рассмотрим, как изменяются механические характеристики двигателя при вводе дополнительного сопротивления в цепь якоря.

Уравнение естественной характеристики

или

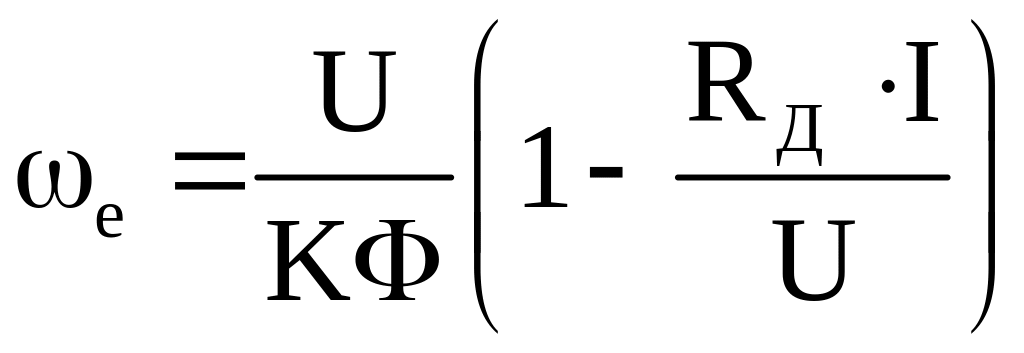(3.23)

В случае включения в якорную цепь дополнительного резистора R_P двигатель будет работать на реостатной характеристике, для которой

(3.24)

При делении (3.24) на (3.23) получим

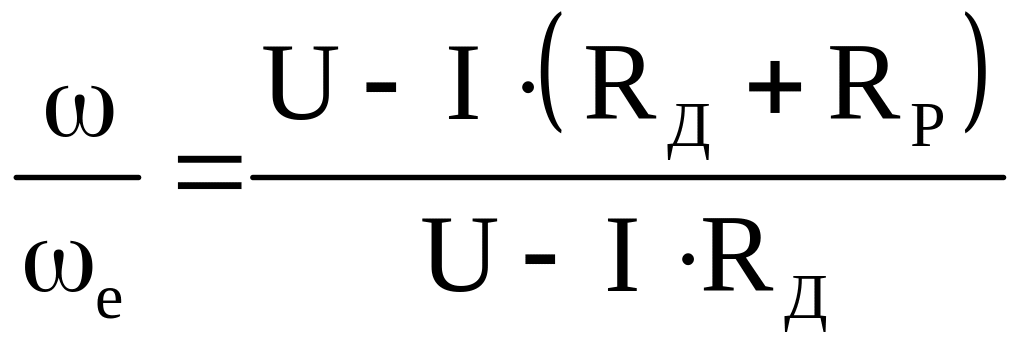
или в относительных единицах

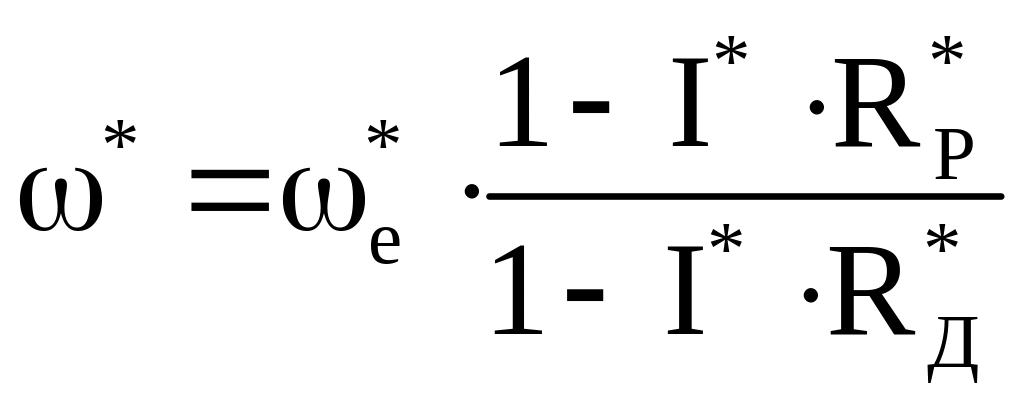(3.25)

Здесь 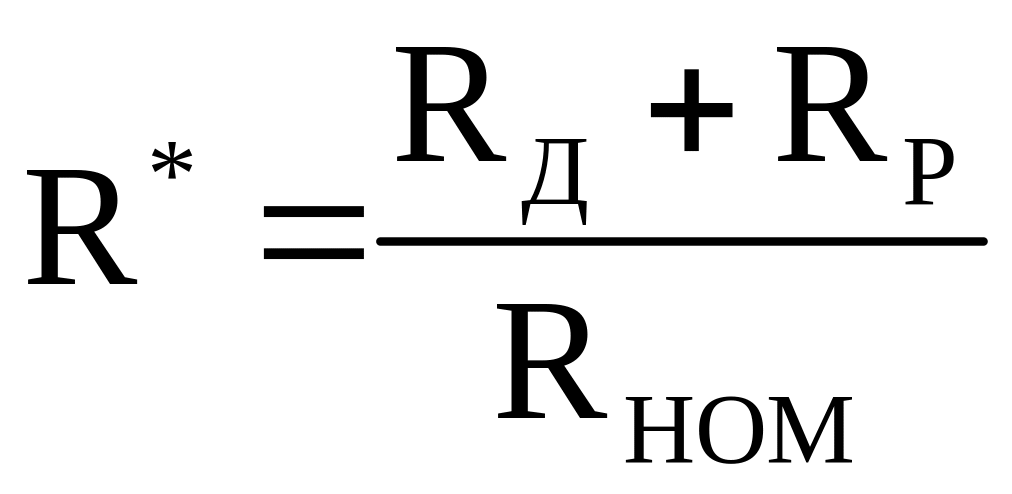– суммарное сопротивление якорной цепи в относительных единицах; , , ,

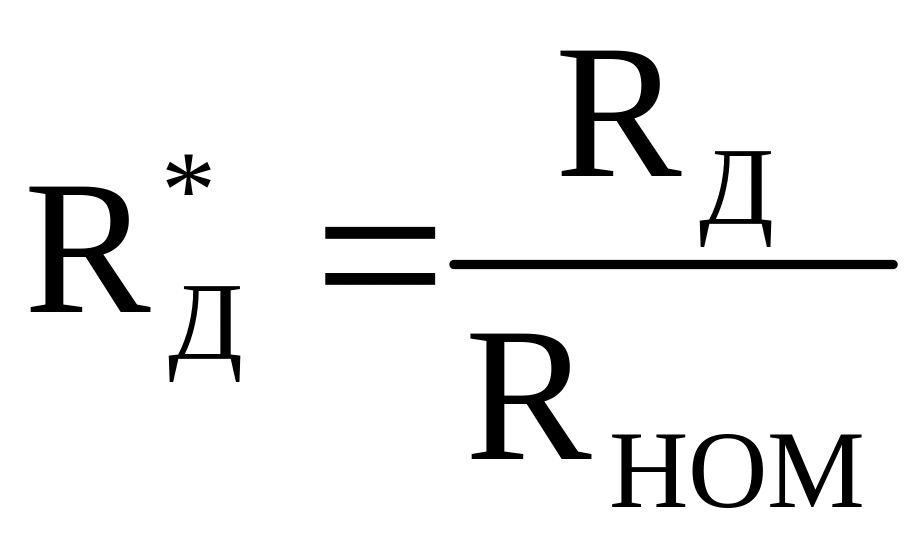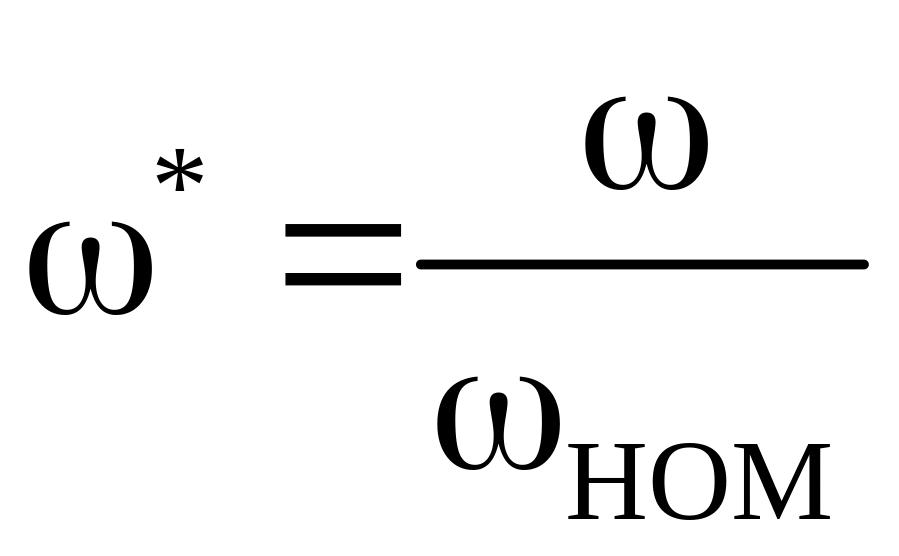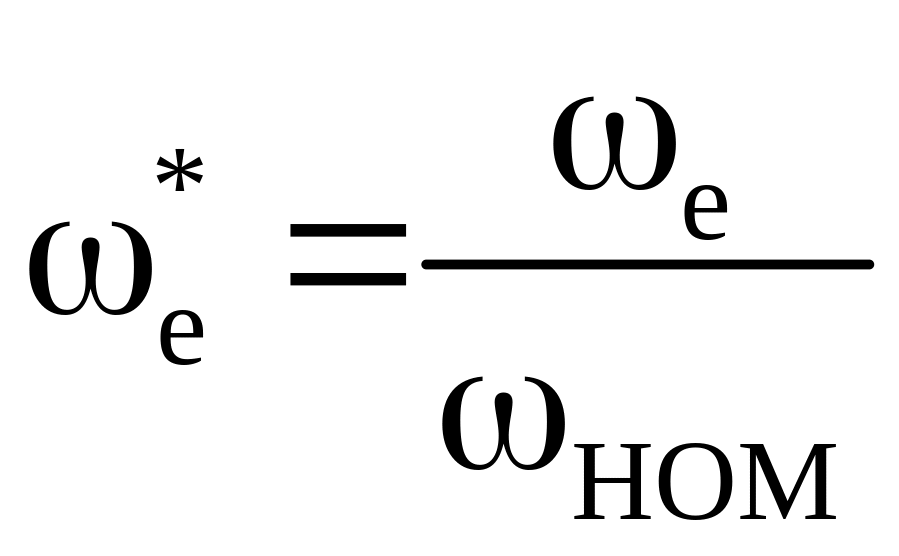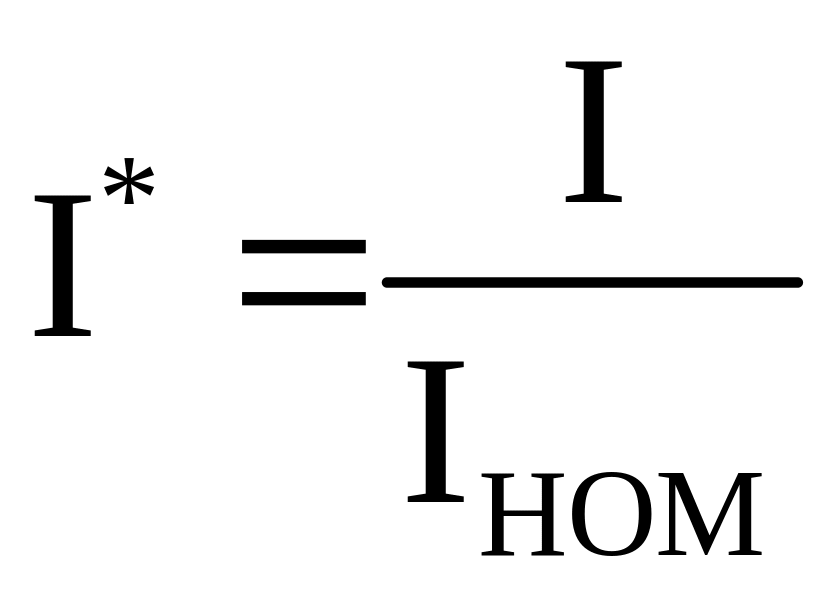
Порядок построения реостатной характеристики сводится к тому, что, задаваясь некоторыми произвольными значениями тока , по имеющейся естественной характеристике находят . Затем по (3.24) при определенном (для которого строится реостатная характеристика) и том же определяют искомое значение . Таким же образом для других значений I^*, определяют искомое значение , и т.д.

Так как

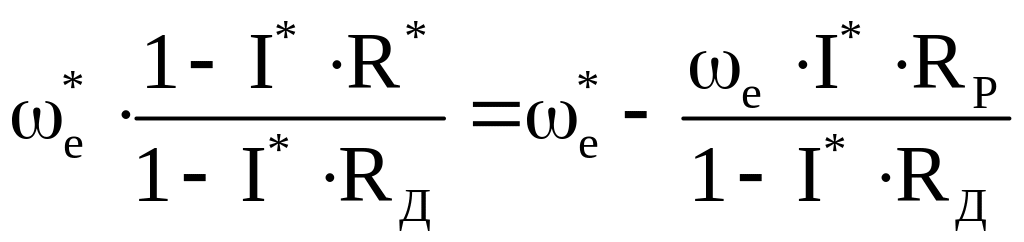, (3.26)

то нетрудно доказать взяв производную , что величина 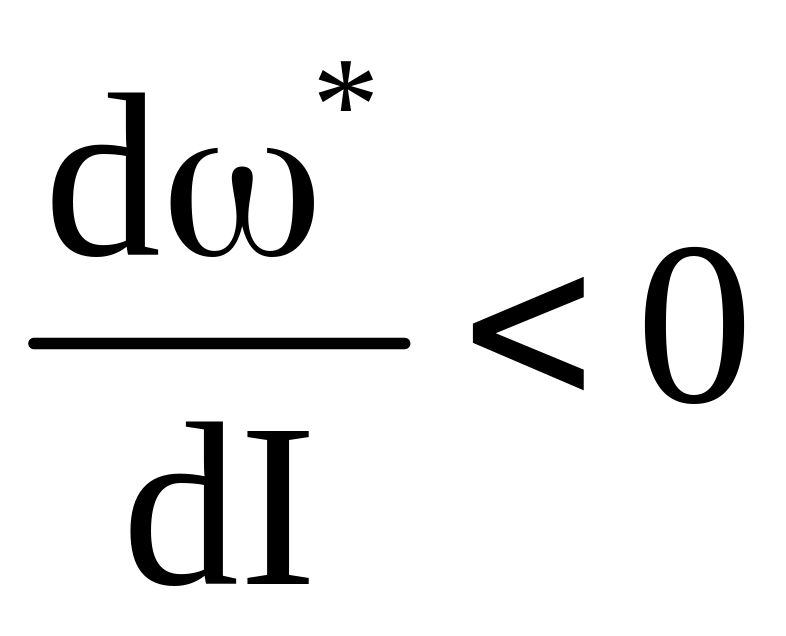, и по абсолютной величине увеличивается с уменьшением I^*. Следовательно кривая и для одних и тех же значений I^*

.

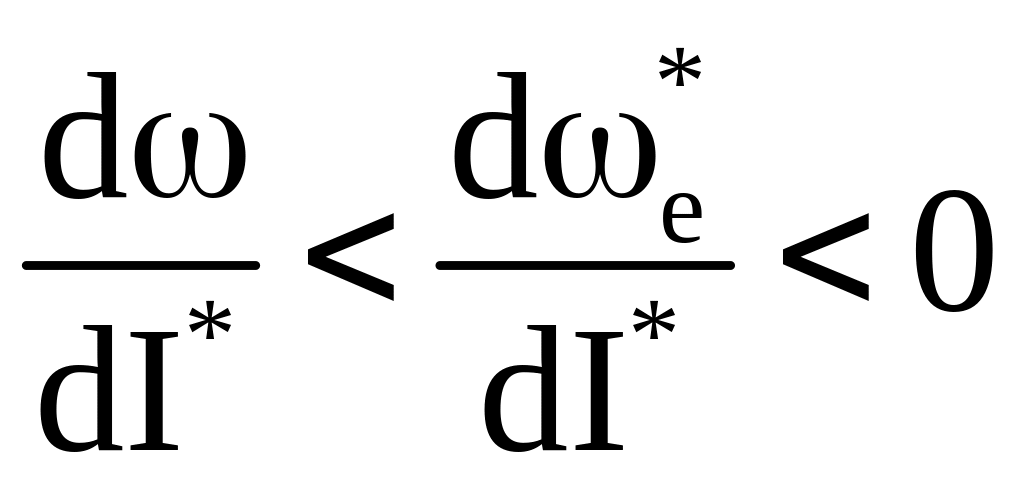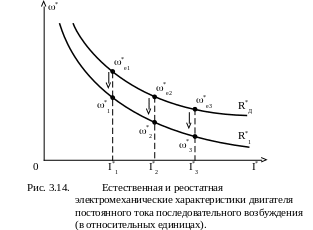
Построив реостатную характеристику ^* = f(I^*) можно описанными выше способами построить характеристику М^* = f(^*) при добавочном сопротивлении в цепи ротора. Очевидно она также будет располагаться ниже естественной,

и .

Как и для двигателя независимого возбуждения увеличивая R_P можно обеспечить торможение противовключением при малых тормозных моментах и токах.

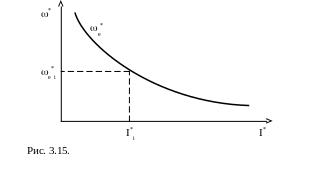
Алгоритм построения реостатной механической характеристики по заданной универсальной характеристике ^*_е = f(I^*).

1. На рисунке 3.15 показана универсальная естественная характеристика ^*_е = f(I^*). Пусть в цепь якоря двигателя включен дополнительный резистор R₁, Ом.

2. Вычисляем номинальное сопротивление двигателя в относительных единицах

.

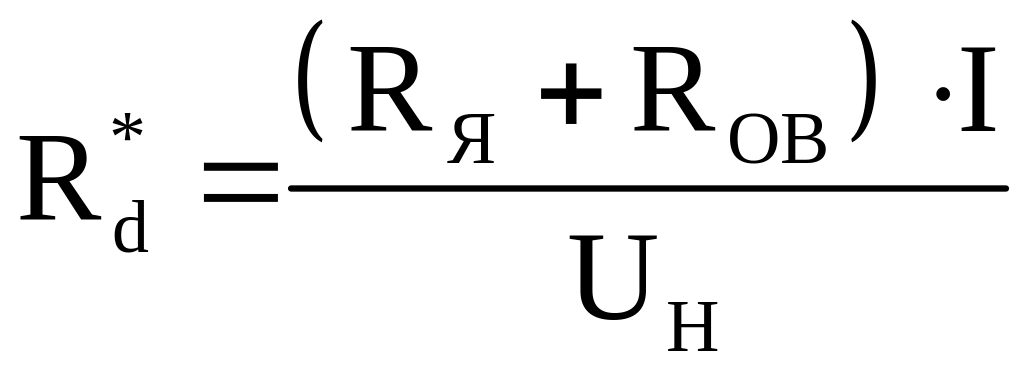3. Вычисляем сопротивление двигателя в относительных единицах при включении дополнительного резистора

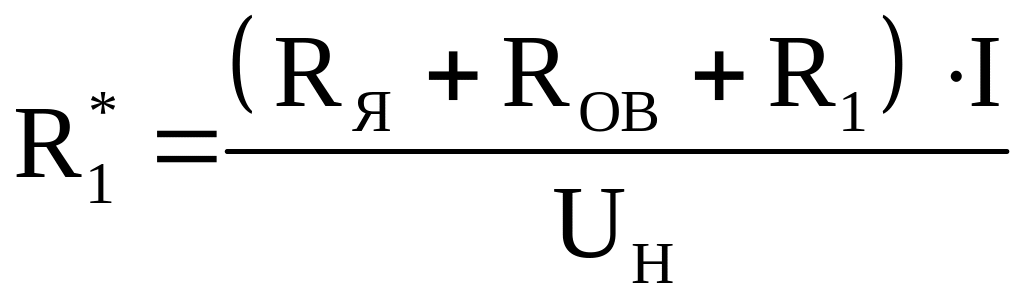
4. Разбиваем ось I^* на n интервалов. Для каждого интервала например i-того, для значения I^*_i определяем по естественной универсальной характеристике _е^*_i.

5. Вычисляем значение скорости при включении добавочного резистора для значения I^*_i

.

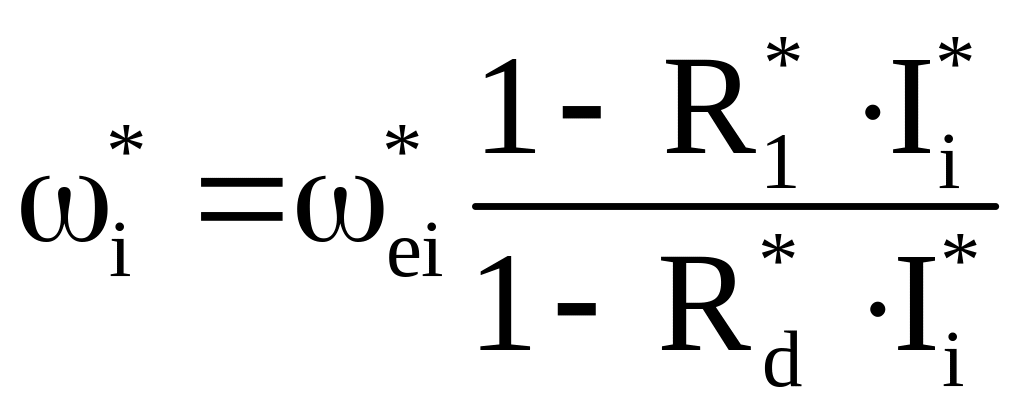6. Повторяя действия по п. 4, 5 для каждого значения I^*_i, где 0 < i  n, получаем точки ^*_i, соединив которые прямой получим реостатную характеристику ^*_R1 = f(I^*).

7. По характеристикам М^* = f(I^*) и ^*_R1 = f(I^*), исключив I^* строим характеристику ^*_R1 = f₁(M^*_R1) или М^*_R1 = f₂(^*_R1).

3.5.2. Шунтирование обмотки возбуждения сопротивлением.

По универсальной характеристике можно найти зависимость произведения конструктивной постоянной двигателя на величину потока якоря двигателя

(3.26)

или если ток задан в относительных единицах

Так как , то

.

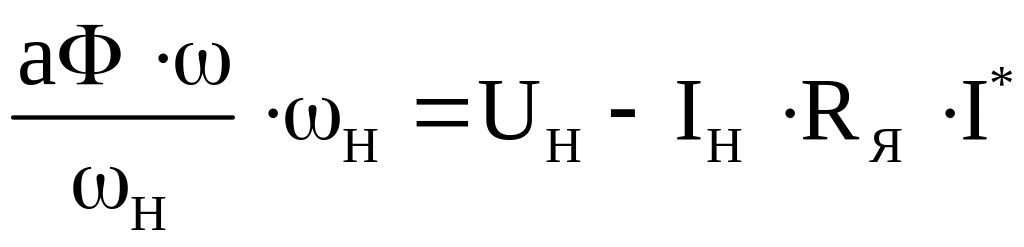Величина ^* берется по зависимости ^* = f(I^*). Откуда

(3.27)

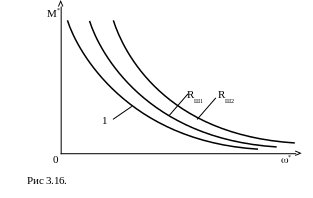
Напомним, что момент двигателя равен М = аФI^*I_H. При шунтировании обмотки возбуждения сопротивлением схема якорной цепи принимает вид, показанный на рисунке 3.16.

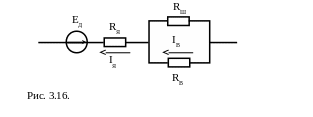
На рисунке: R_B – сопротивление обмотки возбуждения, R_Ш – шунтирующее сопротивление, I_B – ток обмотки возбуждения.

Очевидно, что

Построим зависимость ^*_И = f(I^*) для этого случая. Задаваясь током якоря I^* определяем 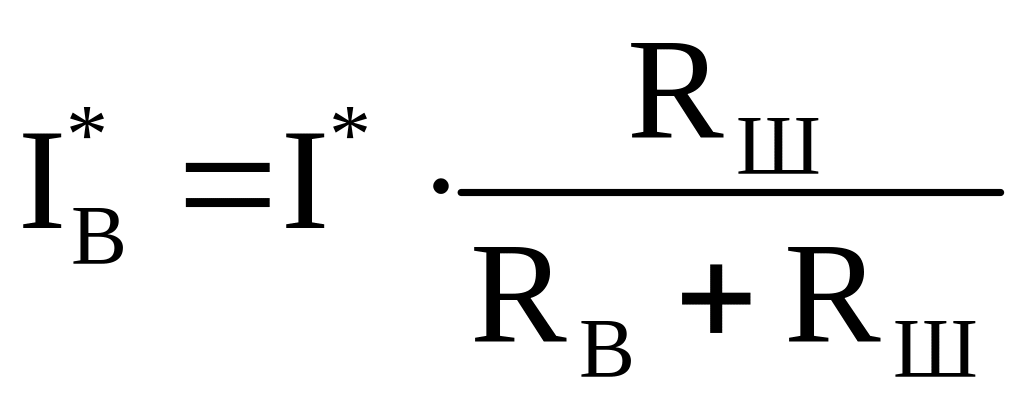, где .

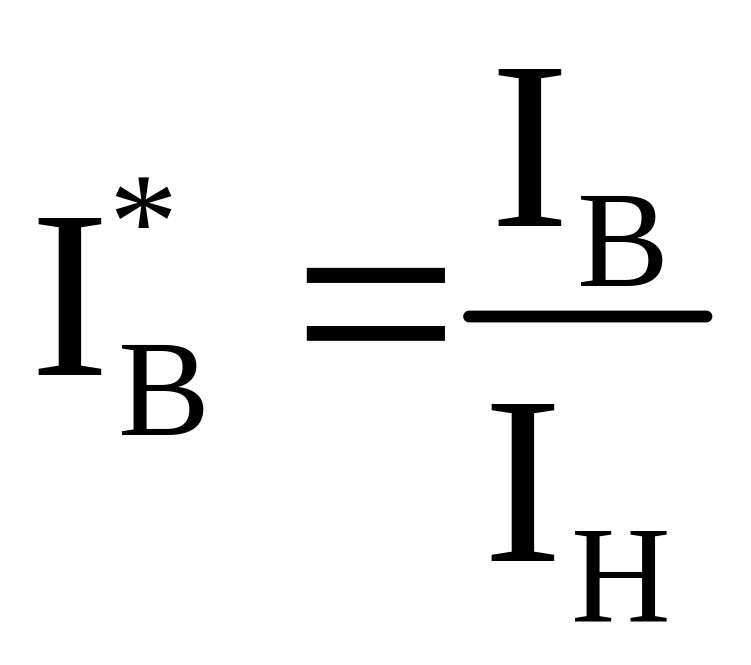Для величины I^*_B и кривой аФ = f(I^*) определяем величину аФ по полученному выше графику аФ = f(I^*). Зная аФ можно определить ^*_Н, соответствующее I^* и заданному значению R_Ш

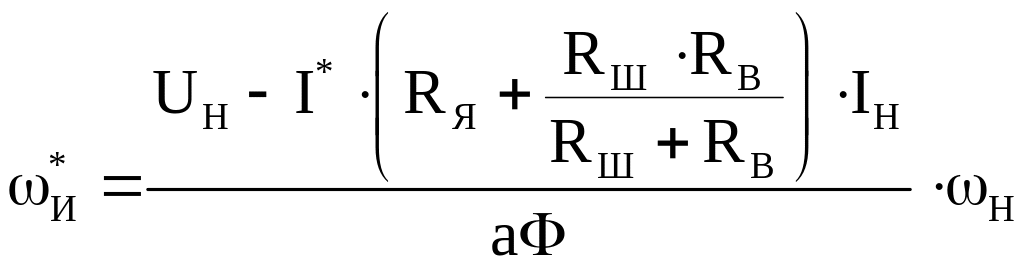(3.28)

Получаем зависимость ^*_И = f(I^*), аналогично получаем зависимость М^* = f(I^*)

По полученным зависимостям ^*_И = f₁(I^*) и М^* = f₂(I^*) можно построить зависимость М^*_И = f₃(^*_И). На рисунке 3.16 показано семейство характеристик М^*_И = f₃(^*_И) для различных значений R_Ш, там же нанесена естественная характеристика 1. Искусственная характеристика при уменьшении R_Ш смещается вверх от естественной причем тем больше, чем меньше R_Ш.

Алгоритм построения механической характеристики двигателя последовательного возбуждения при шунтировании обмотки возбуждения сопротивлением.

1. Задана естественная электромеханическая характеристика двигателя ^*_е = f(I^*)

2. Разбиваем ось I^* на n участков и для каждого участка вычисляем величину аФ_i

,

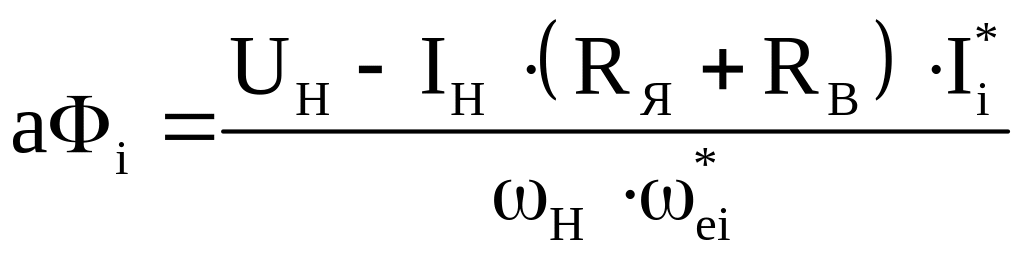где I*i, *ei значение тока и скорости в i-той точке универсальной характеристики.

3. Определяем I^*_Bi для выбранного значения I^*_i

,

где R_Ш – величина сопротивления, шунтирующего обмотку возбуждения.

4. Вычисляем значение скорости двигателя при I^* = I_i и зашунтированной обмотке возбуждения

.

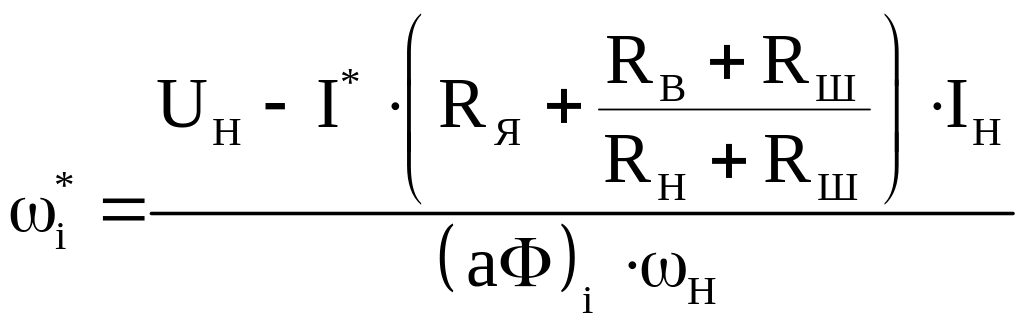5. Определяем значение момента двигателя для этих же условий

.

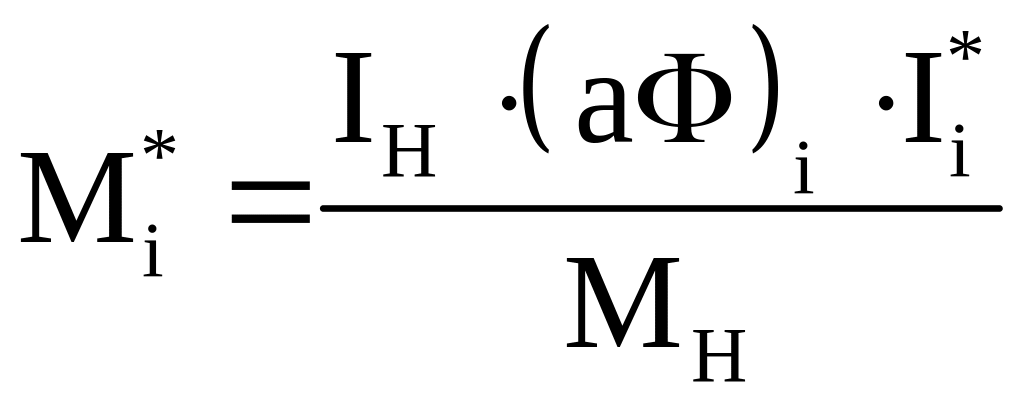6. Повторяя действия для всех точек 0 < i  n строим зависимость ^*_i = f₁(M^*_i) или M^*_i = f₂(^*_i).