Н АЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ

Криворожский металлургический факультет

ТЕОРИЯ

ЭЛЕКТРОПРИВОДА

Методическое пособие для самостоятельной работы студентов

Кривой Рог -2002

Терия электропривода (часть 1.)

Методическое пособие для самостоятельной работы студентов

Составитель: Файнштейн В.Г., доцент, к.т.н.

Рецензент: Учитель А.Д., профессор, д.т.н.

Компьютерный набор, верстка, макетирование: Корнилова О.И.

Утверждено на методическом совещании

КМФ протокол №_____от ______2000г.

ВВЕДЕНИЕ

ПОНЯТИЕ АВТОМАТИЗИРОВАННЫЙ ЭЛЕКТРОПРИВОД

Автоматизированный электрический привод представляет собой электромеханическое устройство, предназначенное для приведения в движение рабочего органа машины и управления ее технологическим процессом.

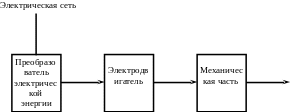
Он состоит из четырех частей: электрического двигателя, осуществляющего преобразование электрической энергии в механическую, преобразователя электрической энергии для питания электродвигателя, механической части, передающей движение рабочему органу машины и системы управления, обеспечивающей оптимальное по тем или иным критериям управление технологическим процессом.

Структурно автоматизированный электропривод имеет вид, показанный на рисунке В.1.

P,U,I,f

,,M

_мех,_мех,M_мех

Рис. В.1. Структурная схема автоматизированного электропривода.

Согласно структурной схемы можно сформулировать основные функции автоматизированного электропривода в технологическом процессе: необходимо обеспечить значения положения, скорости, ускорения рабочего органа, соответствующие требованиям технологического процесса. Так как требования технологического процесса не постоянны, они могут изменяться в функции времени, в зависимости от состояния других агрегатов, входящих в данную технологическую линию и т.д., то автоматизированная система электропривода должна реагировать на эти изменения, поэтому в системе имеются различного рода датчики и задатчики управляющие работой системы электропривода.

По данным ряда авторов электропривод потребляет около 60-65% всей производимой электроэнергии. Поэтому электропривод должен выполнять свои функции с минимальными потерями энергии.

Все эти вопросы изучаются студентами в следующих курсах:

• теория электропривода;

• системы управления электроприводами;

• силовая преобразовательная техника.

Изучение базируется на общетеоретических курсах:

• электрические машины;

• теория автоматического регулирования;

• высшая математика;

• теоретическая механика;

• теоретические основы электротехники.

Задачей курса теория электропривода есть: математическое описание, анализ и синтез силовой части автоматизированного электропривода, включающей в себя преобразователи электрической энергии, электродвигатель и механическую часть электропривода, в том числе выбор электродвигателя и преобразователя электрической энергии

ГЛАВА ПЕРВАЯ

МЕХАНИКА ЭЛЕКТРОПРИВОДА.

1. УРАВНЕНИЯ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ

Механическое движение от вала двигателя к исполнительному органу передается с помощью механического пе­редаточного устройства (МПУ) (см. рис. 1.1), которое в общем случае включает в себя различные механические элементы—шестерни, канаты, валы, муфты сцепления, шкивы и т. д. Эти элементы вращаются или движутся по­ступательно с разной скоростью, имеют определенную жест­кость и момент инерции (массу), а соединения между ними, в общем случае, содержат зазоры. Наличие этих свойств элементов МПУ вносит определенные искажения в процесс передачи движения от двигателя к исполнительному орга­ну и требует соответствующего учета. Анализ механическо­го движения осуществляется с помощью расчетных схем электропривода, получаемых по определенным правилам. Механическое движение элементов электропривода описывается с помощью законов электромеханики. Из кур­са физики известно, что движение материального тела оп­ределяется вторым законом Ньютона, причем уравнение „этого движения имеет вид: для твердого тела, вращающегося вокруг неподвижной оси

, (1.1)

и для поступательно движущегося тела

, (1.2)

где и – векторные суммы моментов и сил, действующих на тело;

J_,m_ – момент инерции и масса тела;

– угловое ускорение вращающегося тела;

– ускорение поступательно движущегося тела.

Эти уравнения позволяют однозначно определить характер механического движения электропривода. Если или > 0 то электропривод совершает движение с ускорением. В другом случае, когда или = 0, электропривод движется с установившейся скоростью или находится в состоянии покоя. Выражения

; (1.3)

называются условиями установившегося движения и в дальнейшем будут часто использоваться. Поскольку при движении тела вокруг неподвижной оси или при поступательном движении тела вдоль прямолиней­ной оси все векторные величины направлены вдоль одной оси, то вместо них можно использовать скалярные величи­ны. Поэтому в дальнейшем не используется запись урав­нений движения в векторном виде. Нахождение зависимостей скорости движения от време­ни (t) и V(t) осуществляется путем решения (интегрирования) уравнений (1.1), (1.2). При этом должны быть известны момент инерции или масса тела, а также характер действующих моментов или усилий. В общем случае моменты и усилия могут зависеть от времени, скорости движения, положения тела в пространстве. Для нахождения измене­ния во времени углового (t) или линейного S (t) положе­ния тела осуществляется интегрирование следующих диф­ференциальных уравнений:

; . (1.4)

В некоторых случаях момент инерции J или масса m может зависеть от времени или положения тела. Эти слу­чаи относительно редко встречаются в практике электропривода .

Напоминаем правило определения знаков скорости, ускорения, моментов. Если скорость, ускорение, момент, сила совпадают с направлением перемещения, то они в уравнении в скалярной форме подставляются со знаком «+», в противном случае со знаком «–».

2. РАСЧЕТНЫЕ СХЕМЫ МЕХАНИЧЕСКОЙ ЧАСТИ ЭЛЕКТРОПРИВОДА.

Элементы механической части привода механически связаны друг с другом и образуют единую кинематическую цепь от двига­теля к исполнительному органу. Каждый эле­мент имеет свою ско­рость движения и характеризуется моментом инерции или массой, а также совокупностью дейст­вующих на него моментов или сил. Дви­жение любого эле­мента описывается одним из уравнений (1.1), (1.2), при использовании которых должно быть учтено взаимодейст­вие этого элемента с остальной частью кинематической це­пи, что удобно осуществлять путем приведения моментов и усилий, а также моментов инерции и масс. В результате выполнения этой операции приведения реальная кинемати­ческая схема заменяется расчетной энергетически эквивалентной схемой, основу которой составляет тот элемент, движение которого рассматривается. Приведение ука­занных величин может быть осуществле­но к любому элементу ме­ханической части электропривода, но, как правило, этим элементом является вал электродви­гателя. Это позволяет наиболее полно ис­следовать харак­тер движения привода и режим его работы, точнее формиро­вать законы движения. Зная параметры кинематической схемы, можно определить и вид движения исполнительного органа. В неко­торых более редких случаях поступают на­оборот, осуществляя при­ведение всех величин к исполни­тельному органу. Для выявления существа операции приведения обра­тимся к рис. 1.1,а, на котором показана кинематическая схема электропривода подъемной ле­бедки. Двигатель ЭД через соединительную муфту Ml, редуктор Р и муфту М2 приводит во вращение барабан Б, на котором навит канат К. К концу каната прикреплен крюк лебедки Кр (исполнительный орган механизма), к которому подвешивается груз массой m. На­грузка электропривода определяется действи­ем силы тяжести, а также трением движущихся частей.

Этот вид нагрузки привода, называемый обычно потерями на трение, учитывается КПД редуктора _Р и барабана _Б. После приведения моментов инерции, масс и сил в схеме рис. 1.1,а, к валу двигателя получаем эквивалентную рас­четную схему рис. 1.1,б, в которой подлежат определению приведенные значения момента нагрузки (сопротивления) М_С и момента инерции. Момент М_С в теории электропри­вода также называют статическим моментом. Приведение момента нагрузки осуществляют исходя из равенства механической мощности нагрузки двигателя в реальной (рис. 1.1, а) и эквивалентной (рис. 1.1, б) схемах. Приведение момента нагрузки выполняют двумя способа­ми в зависимости от направлений потока энергии в механи­ческой части.

Рис. 1.1. Схема механической части электропривода;

а – реальная; б – приведенная расчетная.

Если производится подъем груза, то двигатель совершает полезную работу по подъему груза и покрывает потери мощности на трение в кинематической цепи. Энер­гия направляется от двигателя к исполнительному органу, и баланс мощностей в этом случае имеет вид

;

; (1.5)

где М_С —приведенный к валу двигателя момент нагрузки (сопротивления);  – угловая скорость ротора двигателя; F_и,о – сила тяжести; V_и,о ­– скорость подъема груза; – радиус приведения кинематической цепи между двигателем и исполнительным органом. При опускании груза теряемая им потенциальная энер­гия передается к двигателю. Поэтому потери на трение в кинематической цепи покрываются уже за счет этой энер­гии, и баланс мощностей имеет вид

(1.6)

По аналогии с рассматриваемым случаем, если испол­нительный орган совершает вращательное движение со ско­ростью _и,о и создает при этом момент нагрузки М_и,о, при­веденный к валу двигателя момент нагрузки М_С определит­ся по одной из формул:

(1.7)

(1.8)

где – передаточное число кинематической цепи между валом двигателя и исполнительным органом;  – КПД этой цепи. Формула (1.7) справедлива при направлении потока энергии от двигателя к исполнительному органу, формула (1.8) – при обратном направлении. Приведение моментов инерции и масс элементов осуще­ствляют исходя из равенства запаса кинетической энергии в реальной и эквивалентной расчетной схемах

откуда находим

(1.9)

где J – приведенный к валу двигателя момент инерции эле­ментов –МПУ; J_Д – момент инерции двигателя, муфты Ml и шестерни Z1, J_Б – момент инерции шестерни Z2, муфты М2 и барабана Б. Обобщая полученный результат, заключаем, что для приведения момента инерции вращающегося элемента к валу двигателя следует разделить момент инерции на квад­рат передаточного числа участка кинематической цепи между двигателем и этим элементом, а для приведения массы поступательно движущегося элемента следует умно­жить массу на квадрат радиуса приведения участка кине­матической цепи между двигателем и этим элементом. В результате выполнения приведения по указанным правилам расчетная схема имеет вид рис. 1.1,б. Отметим, что расчетная схема рис. 1.1,б в теории электропривода получила название одномассовой механической системы. Она соответствует механической части привода с абсолют­но жесткими элементами и без зазоров. Применительно к приведенной расчетной схеме рис. 1.1,б уравнение движения в векторной форме имеет вид

(1.10)

Для указанных на рис. 1.1,б направлений моментов двигателя и нагрузки, которые относятся к самому распрост­раненному двигательному режиму работы электропривода, когда движение осуществляется под действием вращающе­го момента двигателя, а момент нагрузки противодействует движению, уравнение (1.10) в скалярной форме записыва­ется как

(1.11)

Правую часть уравнений (1.10) и (1.11) называют ди­намическим моментом, то есть

(1.12)

Основные положения данного параграфа, полученные для наиболее распространенных в настоящее время двига­телей вращательного движения, полностью применимы и к двигателям поступательного движения

3. МНОГОМАССОВЫЕ МЕХАНИЧЕСКИЕ СИСТЕМЫ

Механическая часть электропривода в общем случае со­держит элементы конечной жесткости. Обращаясь к кине­матической схеме подъемной лебедки рис. 1.1,а, в качестве таких элементов можно назвать канат К и валы, соединя­ющие двигатель с редуктором и редуктор с барабаном. При наличии упругих элементов в результате выполне­ния операции приведения в ряде случаев не удается полу­чить одномассовую расчетную схему рис. 1.1, б, и в зависимости от числа упругих элементов получаются многомассовые механические системы – двухмассовая, трехмассовая и т. д. При рассмотрении движения таких систем вводится по­нятие коэффициента жесткости упругого элемента. Он представляет собой коэффициент пропорциональности ме­жду линейной L или угловой  деформациями и возни­кающими в упругом элементе силой F_У или моментом М_У:

(1.13)

(1.14)

Коэффициенты жесткости С₁ и С₂ определяются геомет­рическими размерами упругого элемента и зависят от ма­териала, из которого он изготовлен. Для упругого стержня при его растяжении или сжатии коэффициент жесткости, Н/м, определяется как

(1.15)

где L – длина стержня, м; S – площадь поперечного сече­ния, м²; Е – модуль упругости, Па. Для вала радиусом R при его кручении коэффициент жесткости, Нм,

(1.16)

где – момент инерции поперечного сечения ва­ла, м⁴; G – модуль упругости кручения, Па; L – длина ва­ла, м. Чем больше коэффициент жесткости упругого элемента, тем меньшая деформация в нем возникает. Величина, об­ратная коэффициенту жесткости, носит название податливости. При составлении расчетных схем механической части осуществляется приведение к валу двигателя коэффициен­та жесткости упругого элемента по следующим формулам, которые здесь даются без вывода: для упругого вала при кручении

(1.17)

для упругого поступательно движущегося элемента при растяжении и сжатии

(1.18)

где i,  – соответственно передаточное число и радиус при­ведения кинематической схемы между валом двигателя и упругим элементом.

При параллельном соединении упругих элементов с ко­эффициентами жесткости C₁, С₂, С₃ ... С_n эквивалентная жест­кость определяется по формуле

(1.19)

а при последовательном

(1.20)

Двухмассовая расчетная механическая система получа­ется, если учитывается один упругий элемент в реальной кинематической схеме. Двухмассовая система может быть также получена и при наличии нескольких упругих элемен­тов в кинематической схеме при ее эквивалентировании с помощью формул (1.19) и (1.20).

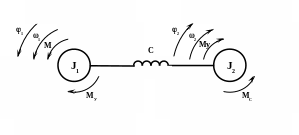
Рис. 1.2. Расчетная схема двухмассовой системы.

Эта система изображена на рис. 1.2. Обычно первую массу J₁ образуют масса рото­ра двигателя и элементов между двигателем и упругим элементом, а вторую массу J₂ – исполнительный орган и элементы между ним и упругим элементом. Обе инерцион­ные массы связаны упругим элементом с коэффициентом жесткости C, и в общем случае их скорости ₁ и ₂, а так­же углы поворота (положения) ₁ и ₂ соответственно не равны между собой. Движение двухмассовой системы описывается следую­щей системой уравнений:

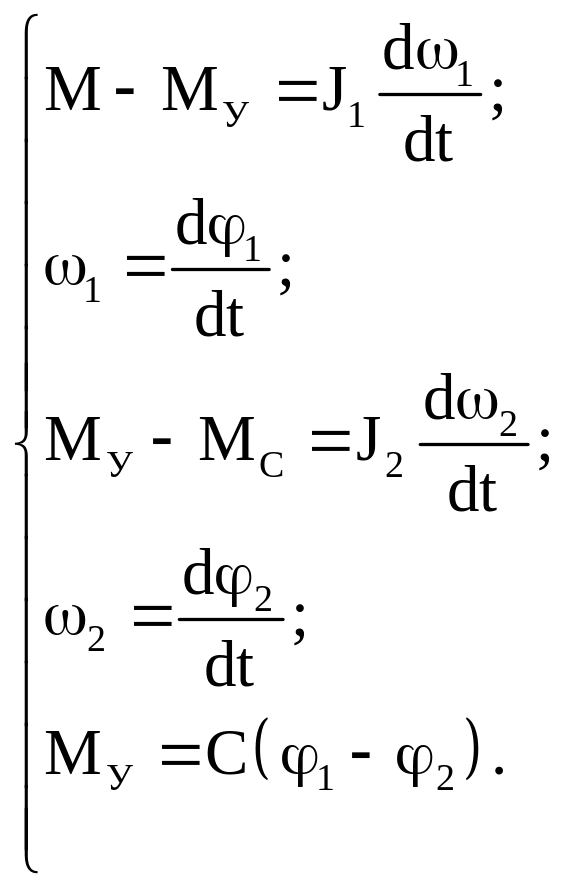(1.21)

Движение двухмассовой механической системы оказы­вается более сложным. Как правило, оно имеет колеба­тельный характер, который определяется процессом обме­на энергией между массами через упругий элемент. При этом может возникнуть явление механического резонанса связанное с резким возрастанием амплитуды движения масс системы. Анализ такого движения достаточно сложен и проводится в фундаментальных трудах по теории элект­ропривода, например в [1 и 2]. Еще более сложное движение имеет место в трехмассовой механической системе, которая получается при учете упругостей двух элементов механической части электропри­вода. По аналогии со схемой рис.1.2 расчетная трехмассо­вая система содержит три массы, соединенные двумя упру­гими элементами, движение которых описывается системой уравнений, аналогичной (1.21). Более подробно о движении трехмассовой системы см. в [3,5]. Многомассовые расчетные схемы получаются и в том случае, когда учитываются зазоры между элементами механической части привода. Приведение зазоров осуществля­ется по следующим правилам: для элемента с вращательным движением и угловым за­зором ₁, рад, приведенное значение зазора , рад; для элемента с поступательным движением и линейным зазором ₂ ,м, , рад. Наличие зазора придает движению нелинейный харак­тер, рассмотрение которого требует специальных матема­тических методов, а в ряде случаев и применения ЭВМ.

Глава вторая установившееся и неустановившееся движение электропривода

2.1. Устойчивость механического движения

В общем случае движение электропривода может проис­ходить в двух режимах – установившемся, при котором скорость движения неизменна (или, в частном случае, рав­на нулю), и переходном (динамическом), характеризую­щемся изменением скорости. В этом параграфе рассматри­вается первый из названных режимов. Условием установившегося вращательного движения в соответствии с (1.11) является равенство моментов двига­теля и приведенного момента нагрузки М=М_С. Проверка выполнения этого условия обычно осуществляется графиче­ски с помощью механических характеристик двигателя и исполнительного органа. Механической характеристикой двигателя вращательно­го движения называется зависимость угловой скорости его вала от развиваемого им момента (М). Для двигателя по­ступательного движения механическая характеристика представляет собой зависимость скорости двигателя от развиваемого им усилия V(F). Различают естественную и искусственную характеристики двигателей. Естественной называется механическая характеристика двигателя, которая соответствует основной схеме включе­ния двигателя, номинальным параметрам питающего напряжения и отсутствию в электрических цепях двигателя дополнительных элементов. На рис. 2.1 показаны естественные характеристики наиболее распространенных двигате­лей вращательного движения: 1 – двигателя постоянного тока независимого возбуждения; 2 – двигателя постоянного тока последовательного возбуждения; 3 – асинхронного двигателя; 4 – синхронного двигателя. Искусственные или, как их еще часто называют, регулировочные характеристики получаются в том случае, когда изменяются параметры питающего двигатель напряжения или в цепи обмоток двигателя вводятся дополнительные элементы (резисторы, конденсаторы и т. д.), а также при включении двигателя по специальным схемам. Искусственных характеристик у двигателя может быть много. По аналогии с двигателем, механической характеристикой исполнительного органа рабочей машины называется зависимость скорости его движения от момента или усилия, то есть зависимость _и,о(М_и,о) или V_и,о(F_и,о). На рис. 2.2 пока­заны приведенные к валу двигателя механические характе­ристики (M_С) некоторых исполнительных органов, полученные в результате выполнения операции приведения М_и,о или F_и,о по (1.5) – (1.8). Характеристика в виде вертикальной прямой линии соответствует различным подъемным механизмам. Ее отличительной особенностью является неизменное направле­ние момента нагрузки М_С. Такие моменты называют актив­ными, они создаются за счет действия различных потенци­альных сил – силы тяжести, упругой деформации тел и так далее. Активные моменты при одном направлении движения (подъем груза) оказывают противодействие этому движе­нию, а при другом (спуск груза) – способствуют ему. Характеристика в виде ломаной линии 2 относится к исполнительному органу, сопротивление, при движении ко­торого создается главным образом силами трения. Поэто­му ее часто называют также характеристикой сухого тре­ния.

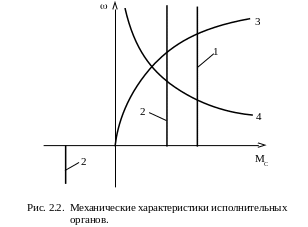
Такой характеристикой (или близкой к ней) обладают механизмы подач станков, горизонтальные конвейеры и транспортеры, механизмы передвижения подъемных кра­нов. Момент нагрузки этого вида всегда направлен навстре­чу движению, поэтому он получил название реактивного момента нагрузки. Кривая 3 характеризует момент нагрузки вентиляторов, центробежных компрессоров, дымососов, который обычно пропорционален квадрату скорости. Характеристики вида 3 часто называют вентиляторными. Характеристикой вида 4, близкой к гиперболической за­висимости, обладают механизмы главного движения токар­ных и фрезерных станков, различные наматывающие уст­ройства. Отметим, что показанные на

рис. 2.1 характеристики представляют собой некоторые идеализированные, теорети­ческие характеристики. Реальный момент нагрузки опреде­ляется, как правило, одновременно несколькими составля­ющими, в силу чего механические характеристики исполни­тельного органа имеют более сложный вид. Для оценки крутизны механической характеристики дви­гателя вводится понятие жесткости, которое определяется как

(2.1)

Используя этот показатель, характеристику синхронного двигателя (прямая 4 на. рис. 2.1) можно назвать абсолютно жесткой (=), двигателя постоянного тока с незави­симым возбуждением (прямая 1) – жесткой, а с последо­вательным возбуждением (кривая 2) – мягкой. Характе­ристика асинхронного двигателя (кривая 3) имеет перемен­ную жесткость — на так называемом рабочем участке (отрезок а-б характеристики) жесткость отрицательна и значительна по модулю, в области критического момента она равна нулю, а при меньших скоростях она положительна и невелика. Имея механическую характеристику двигателя и приве­денную характеристику исполнительного органа (в даль­нейшем характеристику (М_С) будем называть просто характеристикой исполнительного органа), нетрудно опреде­лить выполнимость условия установившегося движения М=М_С. Для этого совместим в одном и том же квадранте эти характеристики. Факт пересечения этих характеристик говорит о возможности совме­стной работы двигателя и ра­бочей машины, а точка их пе­ресечения является точкой ус­тановившегося дви

жения, так как в этой точке М=М_С и d/dt=0. На рис. 2.3 показаны меха­нические характеристики вен­тилятора (кривая 1) и двига­теля независимого возбужде­ния (кривая 2). Точка А является точкой установившегося движения, а ее координаты (_уст, М_уст) – координатами установившегося движения вентилятора.

Наряду с понятием механическая характеристика в теории электропривода широко используется понятие электромеханическая характеристика электропривода, под которой понимается зависимость скорости электропривода от тока электродвигательного устройства. Для полного анализа установившегося движения необходимо определить, является ли это движение устойчивым. Устойчивым будет такое установившееся движение, которое, будучи выведенным из ус­тановившегося режима каким-то внешним возмущением, возвращается в этот режим после исчезновения возмущения. В остальных случаях движение будет неустойчивым. Иллюстрацией устойчивости движе­ния может служить положение равновесия шарика на поверхности: устойчивое на рис. 2.4,а и неустойчивое на рис. 2.4,б. Для определения устойчивости движения удобно вос­пользоваться механическими характеристиками. Оценим в качестве примера (рис. 2.5) устойчивость дви­жения электропривода с асинхронным двигателем АД, при­водящим в движение исполнительный орган с вертикальной механической характеристикой ИО. Установившееся дви­жение возможно с двумя скоростями: _уст1 в точке 1 и _уст2 в точке 2, в которых М=М_С.

Определим, устойчиво ли движение в обоих точках.

Точка 1. Предположим, что под воздействием кратковременного возмущения скорость увеличилась до значения ^’, после чего воздействие исчезло. По механической ха­рактеристике АД скорости ^’₁ будет соответствовать мо­мент М₁^’<М_C. В результате этого динамический мо­мент станет отрицательным, и при­вод начнет тормозиться до скорости при которой _уст1 при которой М=М_С.

Если возмущение вызовет снижение скорости до значе­ния ^’’₁, то момент АД возрастет до значения М^’’₁ >М_C, ди­намический момент станет поло­жительным и скорость увели1чится до прежнего значения _уст1. Таким образом, движение в точке 1 со скоростью _уст1 является устойчивым.

Точка 2. Проведем аналогично анализ устойчивости установившегося движения в точке 2. При повышении ско­рости до ₂ момент АД возрастет до значения М^’₂, динами­ческий момент М_дин=М^’₂–М_С и скорость будет продол­жать увеличиваться, не возвращаясь к своему исходному значению _уст2.

При снижении скорости вследствие снижения момента АД динамический момент будет отрицательным, и процесс снижения скорости, будет продолжаться и далее. Таким образом, можно сделать вывод о неустойчивости движе­ния электропривода в точке 2 со скоростью _уст2. Вследствие отмеченного положения часто участок ха­рактеристики АД с отрицательной жесткостью, на котором расположена точка 1, называют рабочим, а участок с поло­жительной жесткостью, где находится точка 2 – нерабо­чим. Проведенный анализ позволяет определить, что необхо­димым и достаточным условием устойчивости установивше­гося движения является противоположность знаков прира­щения скорости и возникающего при этом динамического момента, то есть

(2.2)

Устойчивость или неустойчивость движения может быть определена и аналитически с помощью понятия жесткости механических характеристик АД и исполнительного органа  и _С. Без вывода приведем условие устойчивой работы электропривода в конечном виде

или (2.3)

Для рассматриваемого примера _С=0, поэтому устой­чивость определяется знаком жесткости характеристики. АД : для точки 1 <0 и движение устойчиво, а для точ­ки 2 >0 и движение неустойчиво. Отметим, что в соответ­ствии с (1.24) при определенной жесткости _С устойчивая работа электропривода возможна и при положительной жесткости механической характеристики АД, в частности на так называемом нерабочем участке характеристики АД.

2. НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ. ЗАДАЧА