III. Отклонение от цилиндричности .

З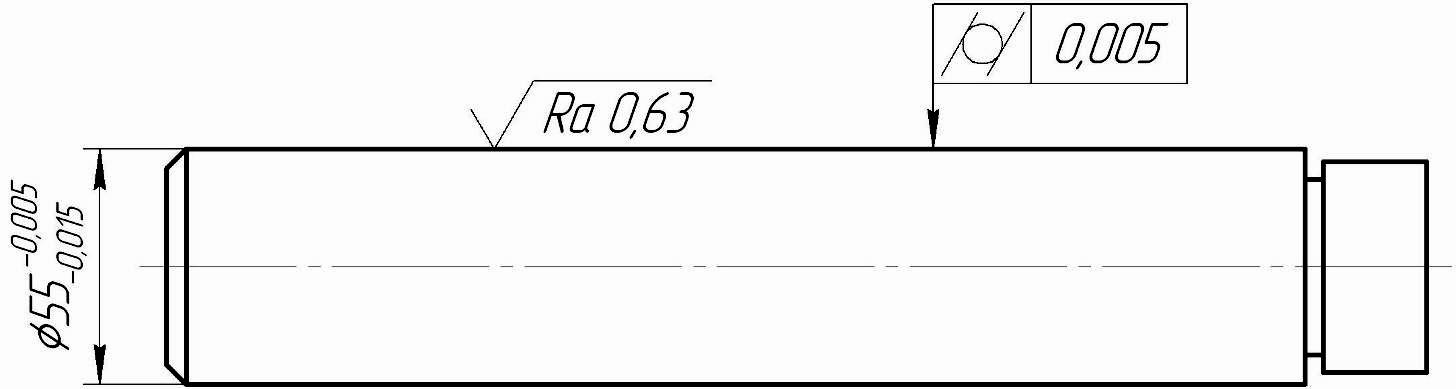 адание №3.1. Измерить отклонение от цилиндричности (определение см. [4, Приложение 1]) поверхности измерительной оправки, используя схему на рис.12. Сравнить полученные результаты с допуском заданным на эскизе:

Оборудование:

1) Плита поверочная чугунная 400х400 ГОСТ 10905-86;

2) Стойка индикаторная (или штатив);

3) Индикаторные головки 1ИГ, 1МИГ и др.;

4) Оправка измерительная.

Известно, что величина отклонения от цилиндричности ( ) нормируется относительно прилегающего цилиндра. Следовательно, при контроле для выполнения принципа совмещения измерительных и конструкторских баз необходимо каким-либо образом материализовать прилегающий цилиндр (см. примечания в Приложении 1), что требует применения сложных средств и схем измерений, например использование КИМ и др. [2]. Так как в настоящее время такие средства и схемы еще не получили повсеместного распространения на производстве, то чаще всего на практике контроль отклонения заменяют контролем отклонений от круглости и профиля продольного сечения , учитывая, что между ними есть связь.

≈ + _, или точнее ² ≈ ² + ² (1)

При измерении, материализовать прилегающую окружность и прилегающий профиль цилиндра (см. примечание к Приложению 1) значительно легче из-за простоты их геометрической формы. Кроме того, существует множество приближенных методов контроля частных случаев вышеназванных отклонений без использования прилегающих профилей, так называемые «двухточечные » и «трехточечные » схемы.

В данной лабораторной работе рассматриваются некоторые из приближенных методов определения и , которые в большинстве случаев обеспечивают необходимую точность измерений, но все же неизбежно содержат методическую погрешность, обусловленную несовпадением измерительной и конструкторской баз.

Частными случаями отклонений от круглости являются овальность и огранка.

Овальность (рис.8) — отклонение от круглости, при котором реальный профиль представляет собой овалообразную фигуру, наибольший в наименьший диаметры которой находится во взаимно перпендикулярных направлениях.

О гранка (рис.9) — отклонение от круглости, при котором реальный профиль представляет собой многогранную фигуру. Виды огранки отличаются количеством граней. В частности, огранка с нечетным числом граней характеризуется тем, что диаметры профиля поперечного сечения во всех направлениях почти одинаковы.

Рис. 8 Рис.9

С амым простым, но и наименее точным способом измерения формы является 2-х точечная схема измерений и

При овальности (рис. 8) отклонение от круглости можно определить простым измерением диаметров в 2-х сечениях под углом 90º (Рис. 10.а).

(2)

В случае других вариантов отклонений от круглости с четным количеством граней эта зависимость принимает вид (3), а величина при 2-х точечной схеме измерения определяется в сечениях указанных на рис.10. б и 10.в.

(3) , где F- коэффициент (рис.10.б и в), учитывающий количество и угол между направлениями измерений диаметров.

а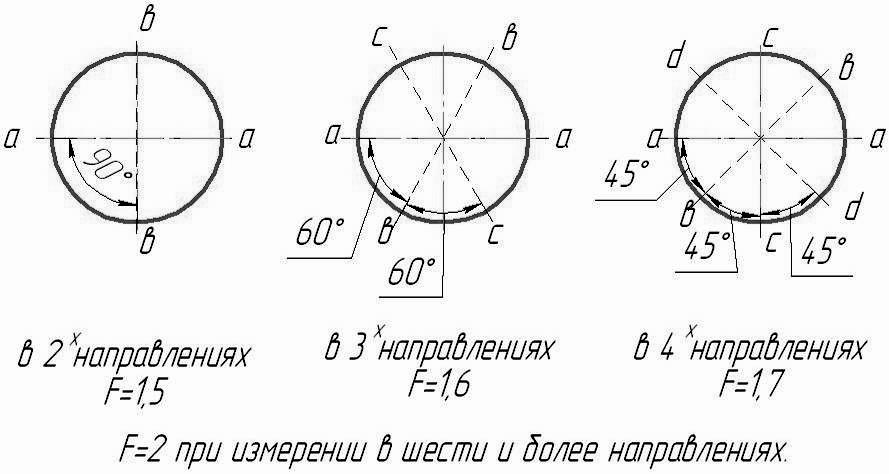 ) в 2-х направлениях; б) в 3-х направлениях (F=1,6);

в) в 4-х направлениях (F=1,7);

Рис. 10. Измерение отклонения от круглости через разницу диаметров.

Частные случаи отклонения профиля продольного сечения показаны на рис.11.

В еличину отклонения для них так же можно определить по разнице диаметров в некоторых сечениях, измеренных в 2-х точечной схеме.

(4)

Конусообразность - отклонение профиля продольного сечения, при котором образующие прямолинейны, но не параллельны (рис.11, а).

Бочкообразность - отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры увеличиваются от краев к середине сечения (рис.11, б).

С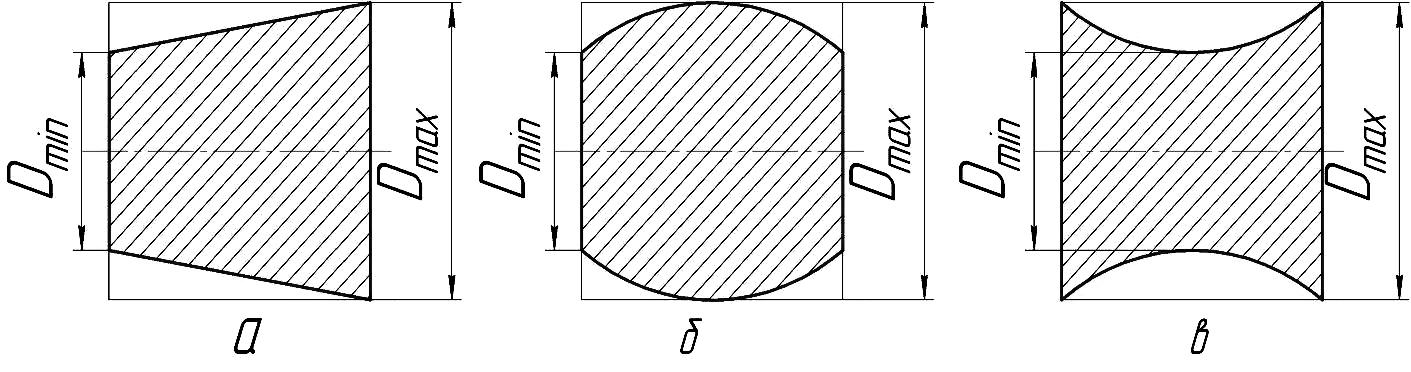 едлообразность - отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры уменьшаются от краев к середине сечения (рис.11, в).

Рис. 11

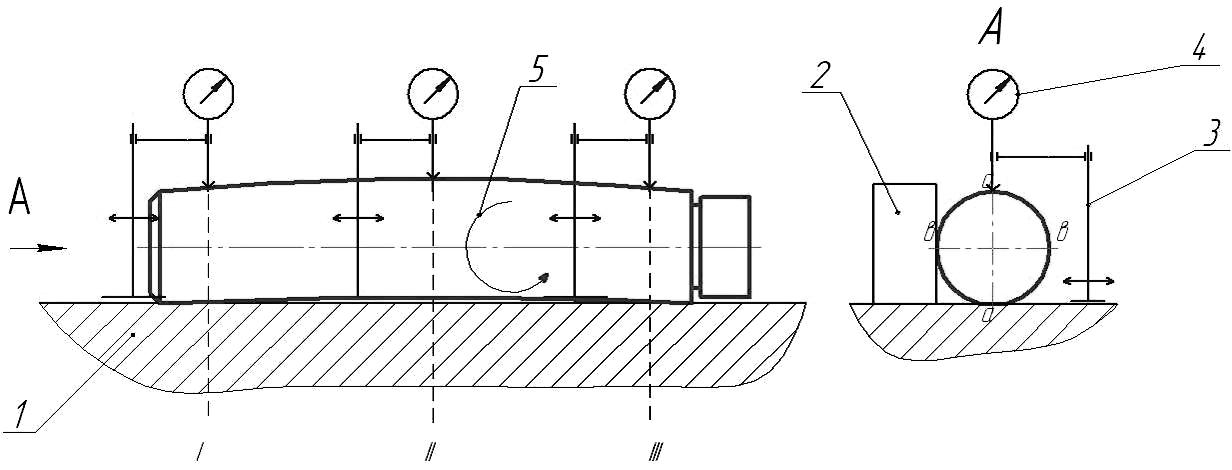
Рис.12

Если же отклонения от круглости и профиля продольного сечения не относятся ни к одному из рассмотренных частных случаев или их характер заранее не известен, то измерение можно провести согласно рис.12, на котором показана реализация той же 2-х точечной схемы.

Плоскость контрольной плиты 1, касательная к поверхности объекта измерения 5, материализует нижнюю образующую прилегающего профиля. Штатив 3 с установленной в нем индикаторной головкой 4 перемещается по поверхности плиты так, чтобы в каждом из сечений I-а, I-b, II-a, II-b, III-a и III-b определить по шкале индикатора 4 разницу расстояний точек верхней образующей оправки от плиты. Измерения а-а и b-b необходимо проводить в 2-х взаимно перпендикулярных сечениях. По формулам (5) и (6) определяются искомые отклонения.

(5) и (6),

Г де - показание измерительного устройства, определяющего колебание расстояния от базовой плоскости до точек верхней образующей объекта. Для формулы (4) max и min значения следует выбирать в парах (I-а и I-b),( II-a и II-b), (III-a и III-b), таким образом, получится 3 величины . Для формулы (5) max и min значения следует выбирать из 3-х значений (I-а, II-a,III-a) и (I-b, II-b,III-b), таким образом, получится 2 величины .

Вычислить величину , квадратично сложив максимальные и по ф.(1).

В качестве индикаторной головки в схеме на рис. 12 могут быть использованы различные средства измерений: индикаторные головки 1ИГ, 2ИГ или 1МИГ (см. Приложение 2), выбор которых зависит от допустимой погрешности измерений (см Приложение 4). В качестве контрольной плиты для измерения небольших деталей можно использовать плоские столики измерительных приборов (оптиметров, микрокаторов, вертикальных длинномеров и т.п.), для измерения крупных объектов больше подойдут поверочные плиты разных размеров.

Задание №3.2. Измерить отклонение от круглости короткой цилиндрической поверхности колеса (рис. 5) или фланца используя трехточечную схему измерения. Сравнить полученные результаты с допуском =0,03мм.

Оборудование: 1) Плита поверочная чугунная 400х400 ГОСТ 10905-86;

2) Стойка индикаторная (или штатив);

3) Индикаторные головки 1ИГ, 1МИГ, ИЧ10 и др.;

4) Комплект призм измерительных.

Трехточечная схема измерения отклонений от круглости является методически более правильной по сравнению с двухточечной. Кроме того, в случае нечетного количества граней на поверхности, 2-х точечную схему использовать нерационально (см. рис. 8 и 9). Примеры применения трехточечных схем измерения отклонений поверхностей валов рассмотрены ниже (рис. 13 и 14).

1) Измерение вала с базированием в призме.

Различают симметричную схему измерения, когда измерительный наконечник располагается по биссектрисе угла α (Рис.13, а) и несимметричную схему, когда измерительный наконечник располагается под углом β к биссектрисе (Рис.13, б).

Измеряемый вал устанавливают в призме и вращают, определяя наибольшее изменение показаний индикаторной головки за один оборот объекта. Отклонение от круглости при этом будет вычисляться по формуле:

(7), где F - коэффициент, который зависит от количества неровностей на периметре детали, угла α или комбинации углов α и β (см. таблицы 3 и 4).

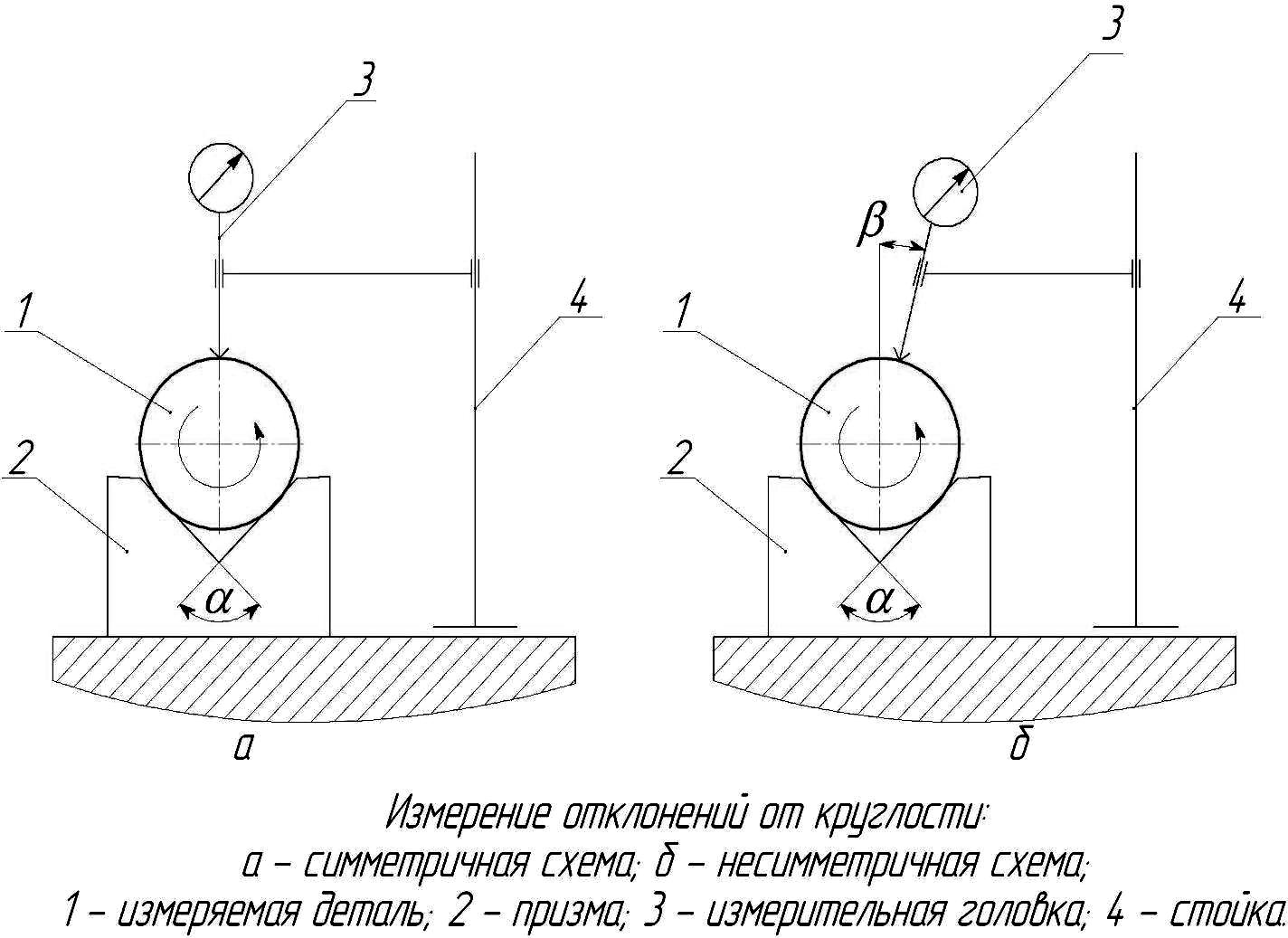
а) симметричная схема б) несимметричная схема

Рис.13. Измерение отклонения от круглости вала в призме:

(1 – измеряемая деталь; 2 – призма; 3 – измерительная головка; 4 – штатив).

2) Измерения вала с применением седлообразной призмы (наездника). Рис.14

Б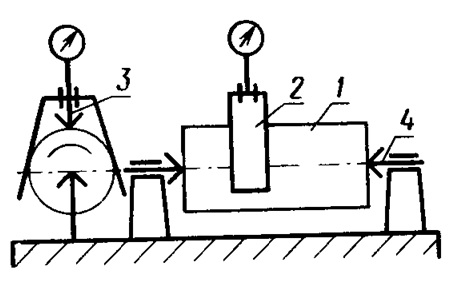 азирование вала 1 может осуществляться по-разному: в центрах 4, в патроне или в призмах, но индикаторное устройство 3 устанавливается в накладной призме 2 (наезднике).

Рис.14. Измерение вала с применением седлообразной призмы.

Вал имеет возможность совершать вращательное движение относительно индикатора установленного в наезднике. На основании разницы показаний индикаторной головки 3 по формуле (6) можно вычислить отклонение. Коэффициент F см. в таблице 5.

Коэффициенты при вычислении отклонения от круглости при симметричной 3-х точечной схеме измерений (рис. 13.а)

Таблица 3

Количество неровностей на периметре n	Поправочный коэффициент для случая
	α = 180º	α = 90º	α = 60º	α = 120º
2 3 4 5	1,38 1,38 * 2,24	1,00 2,00 0,41 2,00	* 3,00 * *	1,58 1,00 0,42 2,00
6 7 8 9 10	* 1,38 1,38 * 2,24	1,00 * 2,41 * 1,00	3,00 * * 3,00 *	* 2,00 0,42 1,00 1,58

Коэффициенты при вычислении отклонения от круглости при несимметричной 3-х точечной схеме измерений (Рис. 13.б)

Таблица 4

Количество неровностей на периметре n	Поправочный коэффициент для случая
	α = 120º β = 60º	α = 60º β = 30º	α = 120º β = 10º
2 3 4 5	2,38 2,00 1,01 2,00	1,41 2,00 1,41 2,00	1,64 0,88 0,96 1,73
6 7 8 9 10	0,42 2,00 1,01 2,00 2,38	0,73 2,00 1,41 2,00 1,41	1,08 1,73 0,79 1,35 0,79

Коэффициенты при вычислении отклонения от круглости при симметричной 3-х точечной схеме измерений с наездником (рис. 14)

Таблица 5

Количество неровностей на периметре n	Поправочный коэффициент для случая			Количество неровностей на периметре n	Поправочный коэффициент для случая
	α = 72º	α = 90º	α = 120º		α = 72º	α = 90º	α = 120º
2	1,53	1,0	0,42	9	2,0	*	1,0
3	2,62	2,0	1,0	10	2,7	1,0	0,42
4	2,38	2,41	1,58	11	2,0	2,0	*
5	1,0	2,0	2,0	12	0,47	2,41	*
6	0,38	1,0	2,15	13	0,62	2,0	*
7	0,62	*	2,0	14	0,38	1,0	0,42
8	0,47	0,41	1,58	15	1,0	*	1,0

Примечание: Для случаев отмеченных * отсутствует изменение показаний измерительной головки.

Кроме рассмотренных выше схем, для определения величины отклонения от круглости применяются специальные средства тем или иным образом материализующие прилегающую окружность (кругломеры). При этом измерительной базой становится именно прилегающая окружность, что полностью соответствует стандартному описанию искомой погрешности. Таким образом, методическая составляющая погрешности измерений становится практически равной нулю, что существенно увеличивает точность измерений, необходимую в особо ответственных случаях.

Рис. 15. Измерение с применением образца круглости.

(1 – измеряемая деталь; 2 – образец круглости «калибр-кольцо», материализующий прилегающую окружность; 3 – измерительная головка.)

С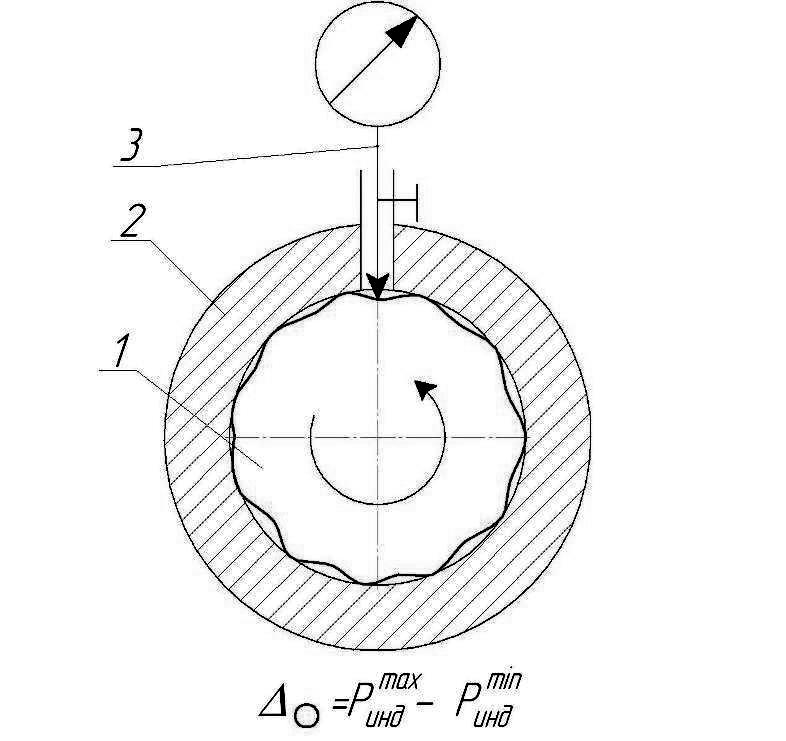 хема измерения показана на рис.15. Измеряемая деталь сопрягается с образцовой по форме деталью (кольцом или пробкой), которая в ограниченном диапазоне диаметров материализует прилегающую окружность. Измерительной головкой, закрепленной неподвижно на образцовой детали, регистрируется максимальная разность показаний за один оборот измеряемой детали относительно образцовой. Для более полной компенсации действительных отклонений диаметра деталей применяют образцовые детали, регулируемые по диаметру, либо набор различных по диаметру образцовых деталей.