2. Двоїстість у задачах лінійного програмування

Кожній задачі лінійного програмування можна поставити у відповідність іншу задачу лінійного програмування, яка називається двоїстою до даної. Теорія двоїстості дає змогу відповісти на деякі питання, пов’язані з властивостями планів задачі лінійного програмування, умовами існування розв’язку та його залежності від даних задачі, пошуком ефективних прийомів знаходження оптимального розв’язку.

Щоб краще зрозуміти поняття двоїстості, виклад почнемо з задачі про використання сировини з найбільшим прибутком. Подамо цю задачу в такій інтерпретації. Чотири підрозділи великої корпорації об’єдналися для виготовлення продукції двох видів П₁ та П₂. При цьому використовуються чотири види сировини S₁, S₂, S₃, S₄, кожна з яких належить окремому підрозділу. Запаси сировини та їх витрати на виготовлення одиниці кожного виду продукції задані в таблиці:

Вид продукції Запаси сировини	П1	П2
S1=8	p11=2	p12=1
S2=6	p21=1	p22=1
S3=5	p31=1	p32=0
S4=7	p41=0	p42=1
Прибуток від одиниці продукції	7	6

Там же вказано прибуток підприємства від виготовлення одиниці продукції кожного виду. Математичне формулювання задачі має такий вигляд.

Серед всіх невід’ємних розв’язків системи нерівностей

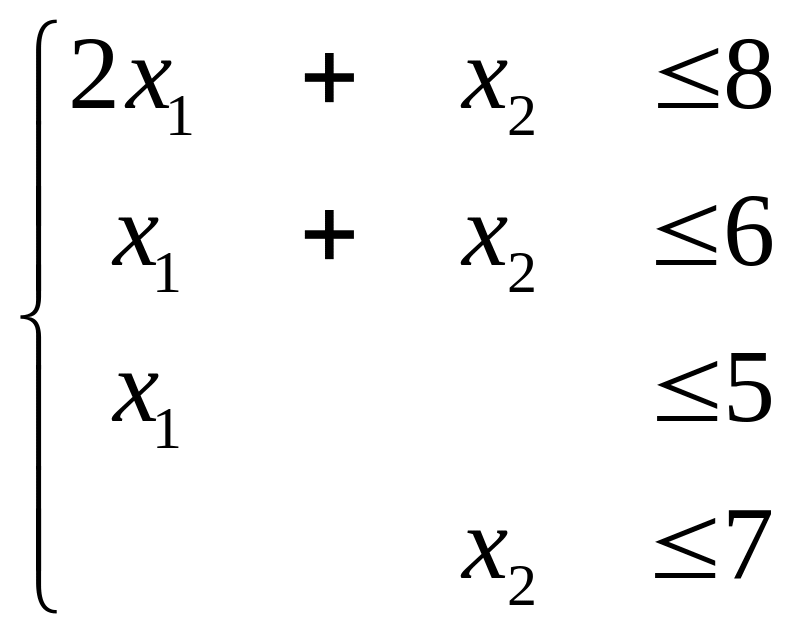, (2.1)

знайти такий, при якому цільова функція

(2.2)

матиме найбільше значення.

Розв’язання цієї задачі привело нас до висновку, що потрібно виготовити одиниць продукції виду П₁ і одиниць продукції виду П₂. При цьому прибуток від реалізації виготовленої продукції буде максимальним і становитиме y. o.

Припустимо тепер, що керівництво корпорації з певних причин приймає рішення не випускати більше продукції видів П₁ та П₂, а наявні запаси сировини продати іншим підрозділам корпорації. Виникає питання: за якими цінами має бути продана сировина? Тобто, нас цікавитиме не вартість сировини при її придбанні корпорацією (ця вартість, по суті, внесена в прибуток, який підприємство отримує при реалізації виготовленої продукції), а, так би мовити, відносна вартість сировини з точки зору прибутків, що їх отримує корпорація в результаті переробки сировини в продукцію. Отже, позначимо через ціну одиниці сировини відповідного виду. Тоді прибуток від продажу сировини, що витрачається на виготовлення одиниці продукції П₁, дорівнюватиме . Природно, що рішення продати сировину, з одного боку, не повинно торкатися інтересів тих підрозділів, що випускали цю продукцію. Отже, прибуток від продажу сировини не повинен бути меншим прибутку від реалізації виготовленої продукції, тобто повинна виконуватися нерівність

. (2.3)

Аналогічні міркування відносно одиниці продукції П₂ приводять ще до однієї нерівності

. (2.4)

З іншого боку, загальна вартість всіх запасів сировини складає І ця вартість повинна бути по можливості найменша, оскільки продаж-купівля відбуваються в межах одної корпорації, яка зацікавлена в максимальному збалансуванні інтересів продавця і покупця.

Таким чином, ми приходимо до такої задачі лінійного програмування:

знайти

(2.5)

за обмежень

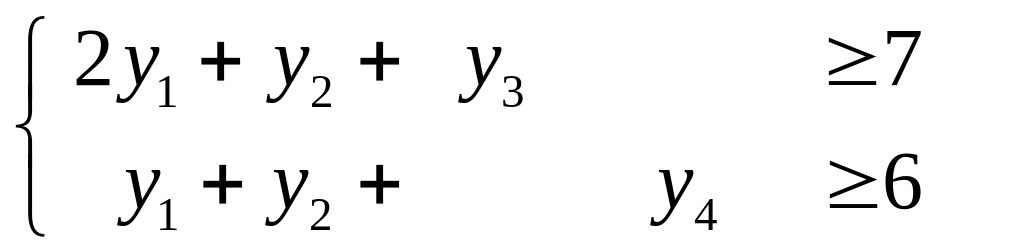, (2.6)

(2.7)

Ця задача є двоїстою до задачі використання сировини, вона має розв’язок (його можна знайти симплексним методом) За цим розв’язком Зовсім не випадково це значення виявилося таким самим, як і значення функції при і , знайдене раніше. Можна вважати, що оптимальний розв’язок двоїстої задачі визначає відносну вартість сировини з точки зору прибутків, що отримує корпорація переробкою сировини в продукцію П₁ та П₂. Найбільша ціна сировини S₂ обумовлена тим, що запаси саме цієї сировини найбільшою мірою обмежують кількість виробленої продукції, а отже, і отримуваний прибуток від її реалізації.

При уважному аналізі прямої та двоїстої задач виявляється, що вони пов’язані рядом суттєвих особливостей.

Перейдемо до загальних означень. Розглянемо спочатку випадок, коли задача лінійного програмування записана в стандартній формі.