§ 2.12. Примеры энергетического расчета оэп в режиме обнаружения Пример 1
Техническое
задание. Рассчитать диаметр входного
зрачка оптической системы прибора,
обеспечивающего максимальную дальность
обнаружения
при
и
.
Оптическая
система прибора
изображена на рис.
2.11 и имеет следующие параметры:
;
;
;
.
В качестве ПЛЭ
используется
охлаждаемое фотосопротивление
(195К)
с входным окном
- фильтром из
германия, просветленного
.
Толщина фильтра
1мм.
Размер чувствительной
площадки ПЛЭ
.
Паспортная
интегральная чувствительность
,
измеренная
по АЧТ (500К), составляет
.
Постоянная времени ПЛЭ
.
Спектр шума для площадки
приведен в [5].
Просмотр поля
обзора осуществляется за счет
строчно-кадровой
развертки. Угловая скорость поворота
оптической оси прибора в направлении
строки
.
Объект
обнаружения - плоский диффузный излучатель
с площадью
излучающей поверхности
.
Температура поверхности
,
коэффициент излучения
.
Положение объекта в пространстве
характеризуется горизонтальным
направлением нормали
к поверхности излучения.
Обнаружение должно
осуществляться в любое время года,
круглосуточно, на высотах
,
при температуре воздуха на уровне моря
,
при относительной влажности, не
превышающей 60%, и
положении линии визирования относительно
нормали к
излучающей поверхности в диапазоне
углов
.
Облачный фон - стационарный, с пространственным энергетическим спектром, описываемым выражением (1.3). В качестве модели функции рассеяния оптической системы принять симметричную двумерную экспоненту.
Электронный тракт прибора предполагается реализовать в виде оптимального фильтра.
Последовательность расчета
1. Поскольку техническим заданием заданы величины и , то правило выбора решения базируется на критерии Неймана-Пирсона. По формуле (2.32) для этого критерия находим требуемое отношение сигнал/шум на входе порогового устройства:
.
По
таблице, взятой из [5], определяем значения
аргументов функции Лапласа при значениях
самой функции, равных 0,95 и 0,05. Получаем
и
.
Следовательно,
.
2. Используя формулу (2.78), рассчитываем модуль спектра полезного сигнала на выходе ПЛЭ. Для этого предварительно следует определить значения ряда величин, входящих в формулу (2.78).
а) Определяем значение произведения . В соответствии с (1.16) для этого необходимо:
рассчитать спектры
и
,
что рекомендуется проводить по методике,
изложенной в [6];
рассчитать
спектральную характеристику пропускания
атмосферы для горизонтальной трассы
длиной
на высоте
(см. § 1.3);
задаваясь ожидаемым
значением входного зрачка оптической
системы
,
найти
и
:
(
и
),
а затем рассчитать спектральную
характеристику пропускания оптической
системы. (Такой расчет применительно к
условиям настоящего примера выполнен
в [5]).
Рассчитанные графики показаны на рис. 2.12. Там же дана относительная спектральная характеристика фотосопротивления (195К). Графическое интегрирование дает:
;
,
где
и
-
масштабы по осям координат на рис. 2.12;
и
-
заштрихованные на рис. 2.12 площади.
Тогда в соответствии с (1.16) и данными ТЗ имеем:
.
б) Входной зрачок
в нашем случае имеет кольцевую форму с
внутренним диаметром
и наружным D. Коэффициент
равен отношению площади кольца к площади
круга диаметром D:
.
в) Считая, что для зеркального объектива условие синусов выполняется, получим
.
д) Установить действительный размер аберрационного кружка рассеяния оптической системы прибора на стадии энергетического расчета невозможно, ибо неизвестен один из важнейших ее параметров - диаметр входного зрачка. Поэтому воспользуемся известным выражением [6], определяющим минимальный угловой размер аберрационного кружка для сферического зеркала-объектива:
.
Это дает возможность считать
.
Подставляя в формулу (2.78) значение всех величин, получим
.
где
-
функция, определяющая
изменение амплитуд спектральных
составляющих
сигнала в зависимости от смещения
изображения объекта
с центра площади ПЛЭ в направлении,
перпендикулярном строке.
В
ид
этой функции, представленный на рис.
2.13. показывает, что наилучшие условия
обнаружения имеет место при
.
При
т.е. при смещении изображения
не более чем на одну треть размера
площадки ПЛЭ, полезный сигнал уменьшается
незначительно:
.
Этим уменьшением можно пренебречь. При
сигнал уменьшается в два раза, что
приводит к уменьшению
отношения сигнал/шум в четыре раза.
Поскольку в задании не указано, при
каких смешениях объекта с центра строки
должны обеспечиваться требуемые значения
и
,
то будем вести расчет для
,
т.е. считать
.
3. По формуле (2.83) рассчитаем энергетический спектр помехи на выходе ПЛЭ. Для этого предварительно проведем указанные ниже вычисления.
а)
Найдем величину произведения
по формуле (1.17). Поскольку спектральный
диапазон работы проектируемого прибора
определяется (см. рис. 2.12) коротковолновой
границей пропускания
оптической системы и длинноволновой
границей чувствительности ПЛЭ, то
;
.
К этому диапазону близок диапазон
;
,
для которого в табл. 1.2 указан интервал
дисперсий яркости облачного фона
.
При вычислении
входящих в формулу (1.17) интегралов будем
считать, что спектр фона определяется
спектром излучения Солнца (
).
Тогда (см. рис. 2.14)
,
где
и
-
масштабы построения графика.
Значение интеграла
вычисляем
по методике, изложенной в [6]. Значение
третьего интеграла очень мало отличается
от площади
на рис. 2.12. Поэтому будем считать
.
Принимая
в соответствии с табл. 1.2
,
т.е. значение, которое в пять раз больше
среднего значения дисперсии фона в этом
спектральном диапазоне, получим
б) Определим значение интеграла, входящего в формулу (2.83) (см. рис. 2.15):
,
где
и
-
масштабы по осям координат на рис. 2.15.
Подставляя в (2.83) все необходимые исходные данные, получим:
.
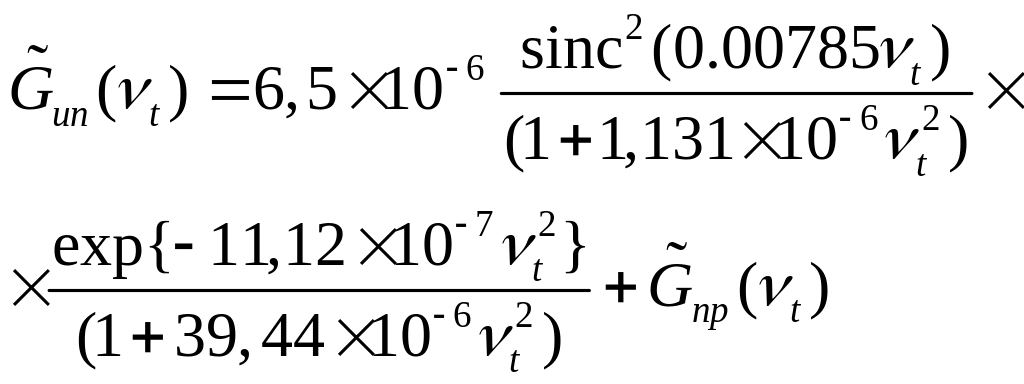4. Подставляя
полученные выражения для
и
в формулу (2.56), находим отношение
сигнал/шум на выходе оптимального
фильтра:
.
Вид
функции
,
которая представляет собой отношение
квадрата модуля спектра полезного
сигнала к энергетическому спектру
помехи на выходе ПЛЭ и является четной
функцией, показан на рис. 2.16. Графическое
интегрирование дает
.
Таким образом,
отношение сигнал/шум, реализуемое на
выходе оптимального
фильтра, оказалось практически равным
требуемому значению
,
и расчет можно считать законченным. При
значительном отклонении
от
расчет пришлось бы повторить, задаваясь
меньшим (при
)
или большим (при
)
значением диаметра зрачка входа
оптической системы.
