§ 2.11. Расчет спектров полезного сигнала и помехи в сканирующих оэп со строчно-кадровой разверткой

Для расчета спектров полезного сигнала и фоновой помехи на входе приемника излучения при линейном сканировании вдоль строки, направление которой параллельно оси X связанной системы координат прибора, могут быть использованы следующие зависимости [10]:

, (2.69)

, (2.70)

где - пространственный яркостной спектр объекта обнаружения, приведенный к плоскости анализа с учетом закона анализа (линейного сканирования);

- пространственный энергетический спектр фона, приведенный к плоскости анализа;

- нормированная некогерентная передаточная функция оптической системы при ;

- передаточная функция анализатора изображения при ;

- линейная скорость сканирования, приведенная к плоскости анализа;

- коэффициент, характеризующий уменьшение пропускания оптической системы за счет экранирования ее входного зрачка;

- апертурный угол объектива в пространстве изображений;

- линейное увеличение объектива по отношению к объекту обнаружения (фону).

Для случая, когда объект обнаружения имеет пренебрежимо малые угловые размеры (“точечный” источник излучения), его пространственный спектр можно представить в виде

,

где и - координаты объекта; - интегральная сила излучения объекта.

Пространственный спектр “точечного” источника, приведенный к плоскости анализа,

, (2.71)

где - редуцированная интегральная сила излучения объекта в направлении линии его визирования (т.е. сила излучения, приведенная к плоскости анализа с учетом спектральных характеристик пропускания атмосферы и оптической системы прибора).

В ТЗ на разработку ОЭП обычно указывается не одно направление, а целая область направлений линии визирования, закоординированная в связанной системе координат объекта обнаружения. В пределах этой области объект должен быть обнаружен с заданными вероятностными характеристиками по любому из направления. Поэтому при энергетическом расчете по индикатрисе излучения объекта выбирается такое значение (и, соответственно, ), которое является минимальным в пределах заданной области.

Для определения нормированной некогерентной передаточной функции оптической системы, которую принято называть оптической передаточной функцией (ОПФ), необходимо знать ее функцию рассеяния, т.е. форму и распределение облученности в аберрационном пятне. Как известно [8, 9, 10] , наибольшее практическое использование имеют два вида аппроксимации функции рассеяния реальных оптических систем: с помощью функции-цилиндра (равномерное распределение облученности в круглом пятне рассеяния) и двумерной экспоненты (гауссоиды) вращения. Для первого случая

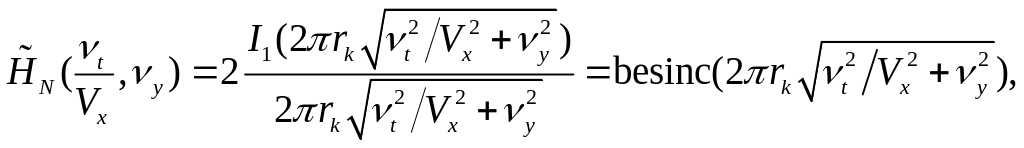(2.72)

а для второго

, (2.73)

где - радиус кружка рассеяния (для первого случая) или радиус, на котором облученность в кружке рассеяния падает в раз по сравнению с центром кружка (для второго случая).

Анализирующим растром (модулятором анализатора изображения) в сканирующих ОЭП является диафрагма, совпадающая по размерам и конфигурации с чувствительной площадкой приемника излучения. Поэтому для ПЛЭ круглой или прямоугольной имеем соответственно [10]:

, (2.74)

(2.75)

где - диаметр чувствительной площадки ПЛЭ; - размеры сторон чувствительной площадки ПЛЭ (размер b- вдоль строки, размер a- перпендикулярно строке).

Подстановка (2.71-2.75) в (2.69) позволяет получить выражения для нахождения спектра полезного сигнала на входе ПЛЭ. К сожалению, точного интегрирования полученных выражений часто выполнить не удается, и для решения задачи необходимо применять численное или графическое интегрирование. Однако при чувствительной площадке ПЛЭ прямоугольной формы и гауссоидальной модели функции рассеяния можно окончательно получить выражение для спектра полезного сигнала. Подставим (2.71), (2.73) и (2.75) в (2.69). Учтем, что

, (2.76)

где - расстояние до объекта обнаружения.

Тогда получим:

.

Поскольку

,

то интеграл в полученном выражении можно представить в виде суммы двух интегралов, второй из которых равен нулю в силу нечетности подынтегрального выражения. Поэтому помня, что

,

можно записать

.

В соответствии в формулой (3.952-7), взятой из работы [4],

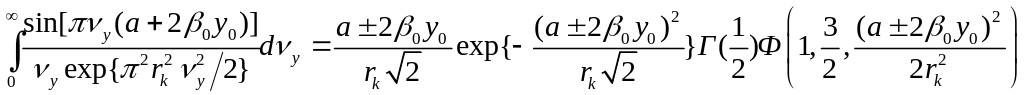
где - гамма-функция; - вырожденная гипергеометрическая функция (функция Куммера).

Известно, что (см. [11]). На основании преобразования Куммера (см. (13.1.27) в [11]).

.

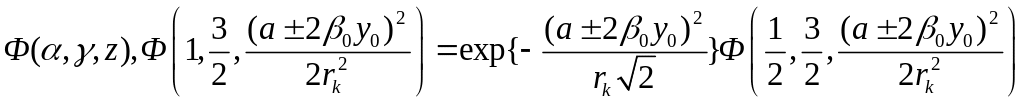Тогда, пользуясь соотношением (13.6.19) из [11] , найдем:

Отсюда получим окончательное выражение для спектра полезного сигнала на входе ПЛЭ для рассматриваемого случая:

(2.77)

где - интеграл вероятностей.

Подстановка (2.77), а также (1.14) при , в (2.53) дает возможность получить выражение для спектра полезного сигнала на выходе ПЛЭ:

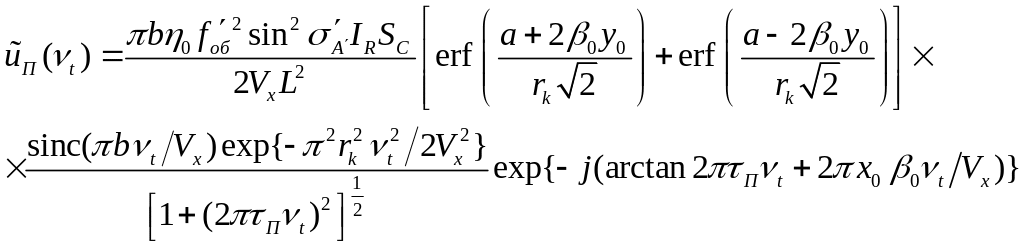(2.78)

Е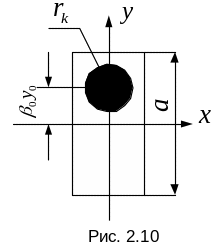 сли объект обнаружения является диффузным излучателем, то произведение рассчитывается по формуле (1.16).

Если площадка ПЛЭ прямоугольная, то окончательное выражение для спектра полезного сигнала может быть получено также для случая равномерного распределения облученности в кружке рассеяния при условии смещения объекта по оси y в плоскости анализа (рис. 2.10). В этом случае размер площадки никак не влияет на

спектр сигнала и вместо передаточной функции (2.75) можно использовать передаточную функцию анализирующего растра, имеющего форму полосы ( ):

. (2.79)

Подставляя (2.71), (2.72) и (2.79) в (2.68) и учитывая (2.76), с учетом фильтрующего свойства -функции получим:

(2.80)

Для спектра сигнала на выходе ПЛЭ имеем:

(2.81)

Для расчета спектра фоновой помехи по формуле (2.70) кроме (2.72) или (2.73), (2.74) или (2.75) должны быть использованы зависимости (1.2), (1.3) или (1.4) при и . Здесь величина определяет дисперсию яркости фона в спектральном диапазоне работы проектируемого прибора, приведенную к плоскости анализа.

К сожалению, получение окончательных выражений для не представляется возможным, и интегрирование должно быть выполнено численным или графическим методами. Найдем формулу для расчета энергетического спектра фоновой помехи на входе ПЛЭ прямоугольной формы для модели фона вида (1.3) при функции рассеяния оптической системы, имеющий вид гауссоиды. Подставим в (2.70) формулы (2.73), (2.75) и (1.3) при и с учетом того, что

,

где - угловой радиус корреляции фона; - расстояние до фона.

Тогда получим

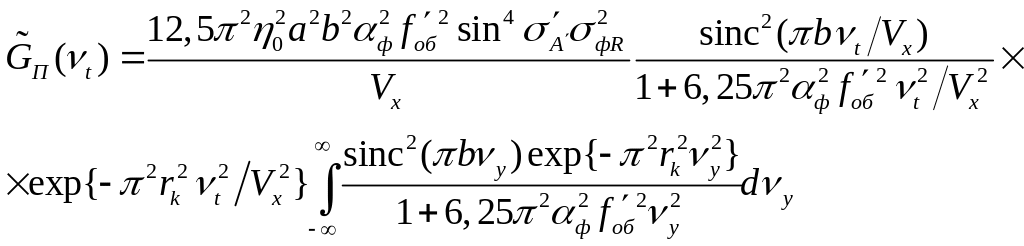(2.82)

На основании (2.54), (2.80), а также (1.14) при , для спектра помехи на выходе ПЛЭ имеем

(2.83)

Для вычисления интеграла в (2.83) необходимо использовать приближенные методы. Однако для идеальной оптической системы ( ) выражения (2.82) и (2.83) можно привести к следующему виду [5]:

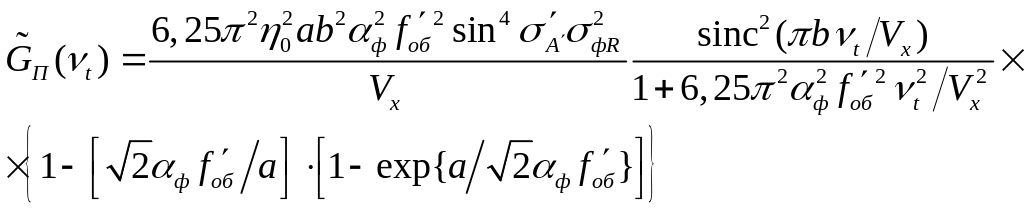(2.84)

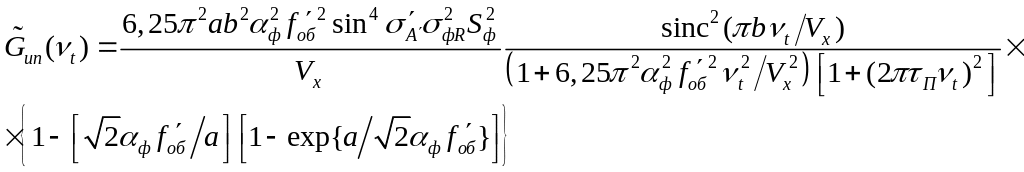(2.85)

Произведение , входящее в (2.83) в (2.80), рассчитывается по формуле (1.17).

Выражения (2.84) в (2.85) могут быть использованы при оценке влияния качества оптической системы на решение задачи обнаружения.