§ 2.9. Передаточная функция оптимального линейного фильтра, и отношение

сигнал/шум на его выходе

Ввиду важности полученных в предыдущем параграфе выражений (2.49) и (2.46), определяющих передаточную функцию оптимального линейного фильтра и отношение сигнал/шум на его выходе, остановимся на них более подробно.

При выводе формулы (2.49) мы не вводили никаких ограничений на закон распределения помехи, действующей на входе фильтра. Поэтому понятие "оптимальный линейный фильтр" следует рассматривать применительно к устройству, относящемуся к классу линейных систем и позволяющему получить на его выходе максимально возможное отношение сигнал/шум по сравнению с любыми другими устройствами этого же класса при произвольном законе распределения помехи на его входе.

Однако отличие закона распределения от помехи нормального не может не внести соответствующих изменений как в процесс расчета вероятностных характеристик ОЭП в режиме обнаружения, так и в процесс оптимизации структурной схемы прибора, рассматриваемый с позиций получения наилучших характеристик. Прежде всего, в этом случае необходимо найти закон распределения помехи на выхода линейного фильтра. Он может не соответствовать закону распределения помехи на входе, ибо из теории вероятностей известно, что такое соответствие имеет место только для нормального закона распределения. После установления закона требуется найти формулы для расчета , соответствующие этому закону. Они уже не будут иметь такой вид, как (2.24), (2.26-2.29) и (2.35), и может оказаться так, что фильтр, оптимальный по соотношению сигнал/шум, не будет оптимальным с точки зрения получения минимальных ошибок обнаружения.

Модуль передаточной функции (2.49), т.е. амплитудно-частотная характеристика (АЧХ) оптимального фильтра, пропорциональная отношению , показывает, что фильтр Можно представить в виде двух последовательно включенных звеньев. Первое звено - помехоподавляющее, с АЧХ вида , коэффициент усиления которого на частоте обратно пропорционален спектральной плотности дисперсии помехи на этой частоте. Второе звено с АЧХ вида играет роль согласованного фильтра, обеспечивающего преимущественное пропускание тех гармоник, амплитуды которых в спектре полезного сигнала на входе имеют наибольшее значение.

В дальнейшем будет показано, что при реальных входных спектрах полезного сигнала и помехи АЧХ оптимального фильтра имеет достаточно сложную форму. Поэтому обычно практическая реализация оптимального фильтра с помощью имеющихся в нашем распоряжении электронных устройств, как правило, встречает серьезные затруднения, если это вообще возможно. Однако это нисколько не умаляет фактического значения теории оптимальной фильтрации. Рассчитав АЧХ оптимального фильтра, всегда можно поставить задачу создания реального фильтра с АЧХ, в той или иной степени, близкой к оптимальной. Такой фильтр иногда называют подоптимальным.

Характеристикой качества любого линейного фильтра (в том числе и подоптимального) может служить, величина

,

показывающая, во сколько раз отношение сигнал/шум , на выходе этого фильтра меньше отношения сигнал/шум на выходе оптимального фильтра. Таким образом, величина выступает здесь в качестве своеобразного мерила потенциальной возможности выделения сигнала из шума при линейной фильтрации (потенциальной помехозащищенности линейных устройств обнаружения). Как мы убедились ранее, при нормальном законе распределения помехи на входе величина может использоваться также для оценки качества прибора как системы обнаружения.

Структура формулы (2.46), которую для удобства воспроизведем еще раз:

,

позволяет высказать несколько общих замечаний.

1. Величина отношения сигнал/шум на выходе оптимального фильтра выражается через входные спектры полезного сигнала и помехи, т.е. учитывает все признаки сигнала: амплитуду (пиковое значение), форму и длительность - и статистические характеристики помехи.

2. Если в спектре полезного сигнала пренебречь гармониками на некотором участке спектра, то значение уменьшается, несмотря на то, что на этом участке спектра сигнал может быть много слабее шума.

3. Если в какой-либо области спектра сигнала шумы отсутствуют, то . Это значит, что шум может быть полностью отфильтрован от части сигнала, лежащей в диапазоне частот, где .

4. Шумы, находящиеся в области частот, где гармонические составляющие полезного сигнала максимальны, снижают наиболее сильно.

5. Наиболее существенное значение для увеличения имеют те частотные области, в которых сигнал в наибольшей мере превосходит шум.

6. Если перед поступлением на вход оптимального фильтра реализация пропускается через любой линейный бесшумный фильтр, то это никак не повлияет на значение . Изменится лишь передаточная функция оптимального фильтра.

7. Если тракт обработки входного воздействия может быть представлен в виде N последовательных линейных бесшумных звеньев (рис. 2.8), причем последнее звено реализовано в виде оптимального фильтра по отношению к действующим на его входе полезному сигналу со спектром и помехе со спектром , то весь тракт является оптимальным фильтром по отношению к его входному воздействию.

Действительно, отношение сигнал/шум на выходе последнего звена

Иными словами, вне зависимости от вида передаточных функций всех предшествующих () звеньев последнее звено корректирует передаточную функцию всего тракта обработки, превращая его в оптимальный фильтр по отношению к входному воздействию, которое характеризуется спектрами и . Проверим это, обозначив передаточную функцию всего тракта через :

.

И поскольку в данном случае в соответствии с (2.49)

то

что соответствует передаточной функции фильтра, оптимального по отношению к спектрам и .

Совершенно очевидно, что передаточная функция последнего (корректирующего) звена при заданных входных спектрах и будет зависеть от вида передаточных функций всех предшествующих звеньев.

В том случае, когда одно звено (или несколько) тракта обработки вносит дополнительные шумы, его оптимизация по отношению к входному воздействию выполнена быть не может. Получаемое на выходе тракта отношение сигнал/шум будет меньше . Предположим, что шумы, статистически независимые от внешней помехи, вносит звено с индексом т. Обозначим энергетический спектр этого шума, приведенного ко входу звена, через . Тогда суммарный шум на входе звена

,

и

.

Отношение сигнал/шум на выходе электронного тракта при оптимизированном последнем звене

,

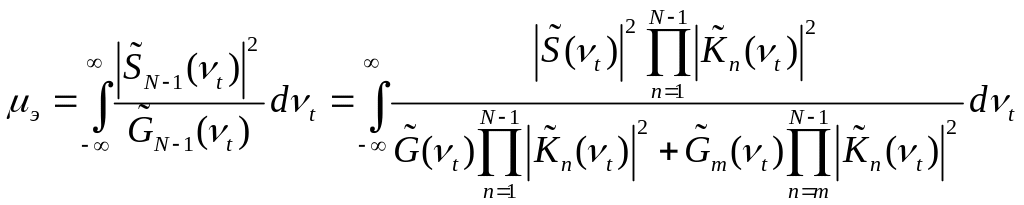откуда следует, что . Равенство имеет место только при .