§ 2.8. Обнаружение методом оптимальной фильтрации

Рассмотренный в § 2.5 метод обнаружения при однократном отсчете реализации, который в практическом исполнении использует непрерывное сравнение мгновенных значений реализации с порогом обнаружения, является наиболее простым: он не требует принципиально никакой специальной обработки входной реализации. Однако поскольку решение выносится на основании одного-единственного значения реализации и для установления порога обнаружения используется одно-единственное значение полезного сигнала, то возможности, потенциально содержащиеся во входной реализации, используются в этом методе далеко но полностью. Характеристики полезного сигнала (например, его форма, длительность и т.д.), которые известны заранее, никак не влияют на процесс принятия решения. По этой причине они не могут оказать влияния на значение, отношения сигнал/шум на входе порогового устройства, т.е. на реализуемые вероятностные характеристики обнаружения.

Поэтому вполне естественно предположить, что применение специальной обработки входной реализации, позволяющий полезно использовать априорно известные данные, т.е. переход к другим методам, обнаружения, улучшить эффективность действия прибора. К таким методам относится метод обнаружения с накоплением, корреляционный метод и метод пассивной фильтрации.

Реализация последнего в наиболее совершенном виде носит название метода оптимальной фильтрации.

Метод накопления в его дискретной форме основан на вынесении решения не по одному отсчету входной реализации, а по сумме n дискретных отсчетов, взятых через одинаковые и достаточно малые интервалы времени. Непрерывная (интегральная) форма метода накопления предусматривает принятие решения по значению интеграла от входной реализации, взятого на некотором интервале времени.

Корреляционный метод может быть использован также в двух формах - дискретной и непрерывной. В первом случае основой для принятия решения является выборка, состоящая из N дискретных отсчетов реализации (выборка объема N). Это приводит к принятию решения по величине (i=1,2,3…N), представляющей сумму N произведений мгновенных значений полезного сигнала и реализации , которые соответствуют моментам времени взятия отсчетов. Для непрерывной формы объем выборки , а решение принимается по величине , т.е. по величине интеграла от произведения , взятому на некотором интервале времени . В определенных условиях значение этого интеграла представляет собой меру взаимной корреляции между реализацией и полезным сигналом , чем и объясняется название метода. Прибор, реализующий корреляционный метод, должен иметь в своем составе специальный "активный" элемент-генератор полезного сигнала . В связи с этим корреляционный метод иногда называют методом активной фильтрации [4].

В силу ограниченного объема настоящего учебного пособия на подробном описании метода накопления и корреляционного метода, а также на достигаемых с их помощью результатах мы останавливаться не будем. Перейдем непосредственно к методу оптимальной фильтрации.

Рассмотрим схему принятия решения, изображенную на рис. 2.7. Аддитивная смесь полезного сигнала и фоновой помехи приходит на вход системы первичной обработки информации (СПОИ). Ока преобразуется этой системой в некоторую случайную реализацию , являющуюся функцией времени и представляющую собой электрический сигнал, снимаемый с ПЛЭ. В силу линейности СПОИ [10], реализация состоит из суммы полезного сигнала и шума , причем учитывает как фоновую помеху, так и собственный шум ПЛЭ. Вид реализации также изображен на рис. 2.7, где пунктиром показан полезный сигнал, пиковое значение которого соответствует времени . Поскольку момент появления цели в мгновенном поле зрения прибора неизвестен, то время является случайной величиной.

Реализация поступает на вход бесшумного линейного электронного фильтра с передаточной функцией , на выходе которого имеем реализацию . Пороговое устройство ПУ выдает решение по методу однократного отсчета, непрерывно сравнивая мгновенное значение реализации с порогом, рассчитанным в соответствии с одним из критериев качества. Таким образом, все формулы для расчета вероятностных характеристик обнаружения, полученные в § 2.5, 2.6 и 2.7, остаются в силе. Необходимо только установить получаемое на входе порогового устройства отношение сигнал/помеха в соответствии с формулой (2.25) и корреляционную функцию помехи на входе ПУ, чтобы найти среднюю частоту ложных тревог в единицу времени, в соответствии с формулой (2.35).

Обозначим спектр полезного сигнала и энергетический спектр помехи на входе фильтра соответственно через и , а аналогичные спектры, корреляционную функцию и дисперсию помехи на выходе фильтра - соответственно через и .

Сигнал запаздывает по отношению к началу входной реализации на время . Поэтому

(2.37)

где - спектр полезного сигнала, рассчитанный в его собственной шкал времени (т.е. момент принят за начало отсчета времени).

Выходные спектры определяются по формулам:

(2.38)

(2.39)

Для полезного сигнала, корреляционной функции и дисперсии помехи на выходе фильтра имеем:

(2.40)

(2.41)

(2.42)

Найдем функцию , которую можно рассматривать как зависимость мгновенного значения отношения сигнал/шум от времени. Из (2.40) и (2.42) найдем

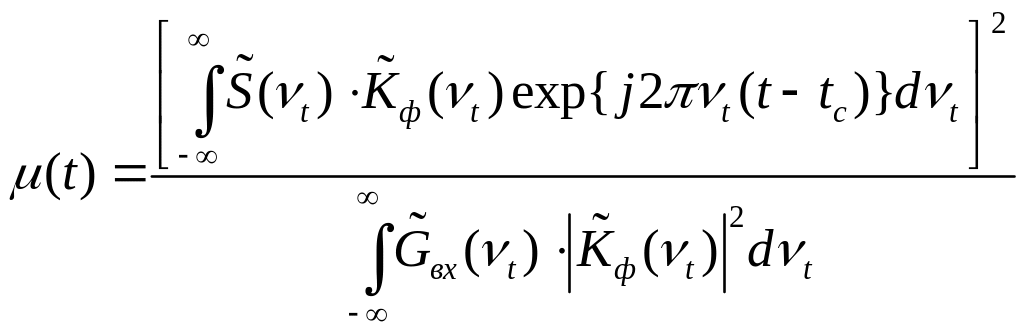. (2.43)

используем известное неравенство Шварца – Буняковского , которое можно представить в виде

,

где и - произвольные комплексные функции временной частоты .

Положим в указанном неравенстве, что

.

Получим

. (2.44)

Поскольку сигнал есть функция вещественная и его квадрат равен квадрату его модуля, то числитель в (2.43) равен левой части неравенства (2.44). Поэтому в соответствии (2.43) и (2.44) можно записать

(2.45)

На основании (2.45) можно сделать очень важный вывод: отношение сигнал/шум на выходе любого линейного фильтра в любой произвольный момент времени не может быть больше величины

(2.46)

В формуле (2.46) мы опустили построчный индекс у . Для удобства записи не будем его использовать и в дальнейшем. Поэтому следует помнить, что функции и определяют спектр полезного сигнала и энергетический спектр помехи на входе фильтра, причем спектр сигнала рассчитывается в его собственной шкале времени.

Теперь можно перейти к решению задачи оптимального синтеза структурной схемы ОЭП обнаружения с позиции максимизации отношения сигнал/шум. Иными словами, перейдем к нахождению передаточной функции такого фильтра, который обеспечивает получение на его выходе максимального значения . Положим в (2.43)

, (2.47)

____________________________

Доказательство справедливости этого неравенства можно найти, например, в [2,15].

где время запаздывания выходного сигнала фильтра по отношению к моменту действия входного сигнала; - функция, комплексно-сопряженная со спектром сигнала. Тогда получим

. (2.48)

Нетрудно видеть, что в момент времени экспоненциальный член в числителе (2.48) обращается в ноль и отношение сигнал/шум на выходе фильтра , т.е. равно максимально достижимому значению. Таким образом, передаточная функция оптимального фильтра определена:

. (2.49)

Интеграл в числителе (2.48) определяет полезный сигнал на выходе оптимального фильтра. Равенство нулю экспоненциального члена в подынтегральном выражения означает, что в момент времени все спектральные составляющие сигнала находятся в одинаковой фазе. Следовательно, в этот момент времени полезный сигнал может быть получен простым суммированием амплитуд его спектральных составляющих, т.е. достигает максимального (пикового) значения.

Из (2.40) и (2.49) при следует:

, (2.50)

т.е. на выходе оптимального фильтра максимальное (пиковое) значение полезного сигнала численно равно произведению .

Корреляционную функцию помехи на выходе оптимального фильтра найдем из (2.41) при . Учитывая, что , получим

(2.51)

Дисперсия помехи на выходе фильтра

. (2.52)

Этот же результат можно было бы получить непосредственно из (2.42).

Таким образом, дисперсия помехи на выходе оптимального фильтра численно равна произведению . Деление квадрата (2.50) на (2.52) дает

.

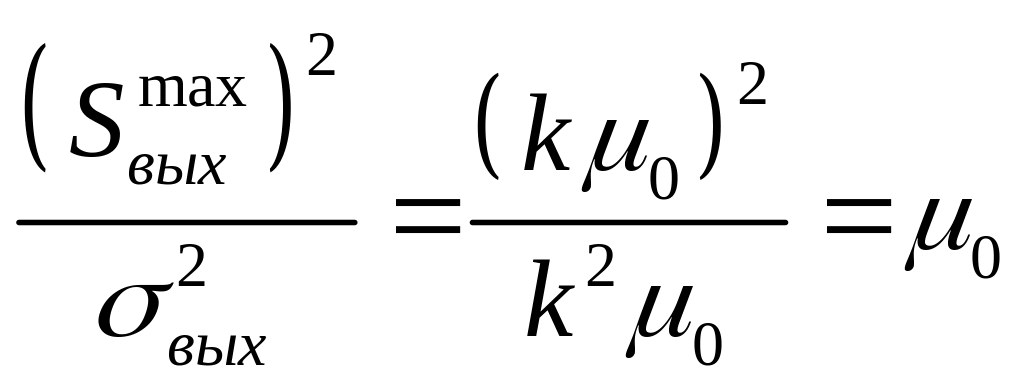Для определения вероятностных характеристик ОЭП обнаружения, использующего метод оптимальной фильтрации, следует использовать выражения (2.24) и (2.28-2.29) при . Нахождение среднего числа ложных тревог в единицу времени или среднего временного интервала между ложными тревогами требует в соответствии с (2.85) и (2.34) определения значения второй производной корреляционной функции помехи на выходе фильтра при . Расчет может быть выполнен по формуле (2.51) при заданных спектрах полезного сигнала и помехи на входе.