Проектировани пеленгационных оэс

Москва, 2007

Оглавление

Глава 1. Математические модели объектов пеленгации, фонов, атмосферы

и приемника лучистой энергии. 2

§ 1.1. Математические модели излучения объектов пеленгации 2

§ 1.2. Математические модели излучения фоновых образований 3

§ 1.3. Расчет спектральной характеристики пропускания атмосферы 6

§ 1.4. Передаточная функция приемника излучения 10

Глава 2. Основы теории энергетического расчета ОЭП в режиме

обнаружения 12

§ 2.1. Постановка задачи 12

§ 2.2. Априорная и апостериорная вероятности. Отношение правдоподобия 13

§ 2.3. Вероятностные характеристики обнаружения 15

§ 2.4. Правило выбора решения и критерии его качества 17

§ 2.5. Обнаружение методом непосредственного сравнения 20

§ 2.6. Отношение сигнал/шум. Рабочие характеристики ОЭП в режиме

обнаружения 24

§ 2.7. Расчет среднего числа ложных тревог в единицу времени 27

§ 2.8. Обнаружение методом оптимальной фильтрации 29

§ 2.9. Передаточная функция оптимального линейного фильтра, и отношение

сигнал/шум на его выходе 33

§ 2.10. Методика энергетического расчета ОЭП в режиме обнаружения 36

§ 2.11. Расчет спектров полезного сигнала и помехи в сканирующих

ОЭП со строчно-кадровой разверткой 39

§ 2.12. Примеры энергетического расчета ОЭП в режиме обнаружения 43

Литература 51

Глава 1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ ПЕЛЕНГАЦИИ, ФОНОВ, АТМОСФЕРЫ И ПРИЕМНИКА ЛУЧИСТОЙ ЭНЕРГИИ

§ 1.1. Математические модели излучения объектов пеленгации

Излучение точек пространства в рассматриваемый момент времени t в спектральном диапазоне характеризуется энергетической яркостью , которая зависит от пространственных координат излучающей точки , направления распространения излучения , метеоусловий.

При пеленгации объектов, расположенных на дистанциях, при которых угловой размер объекта как излучателя значительно меньше углового разрешения оптической системы, говорят, что решается задача пеленгации “точечного” источника с силой излучения . При пеленгации «точечного» источника, несмотря на то что объект пеленгации может иметь самое разнообразное распределение энергетической яркости по площади, оптическая система, являясь фильтром пространственных частот, оказывается неспособной различать детали формы объекта. Подробности формы объекта в этих условиях несут в себе избыточную информацию, которая не используется оптической системой с ограниченной полосой пропускания пространственных частот. Определение значения для таких “точечных” объектов основывается на использовании упрощенной схемы излучателя. Излучающая поверхность объекта пеленгации представляется совокупностью К простейших излучающих поверхностей или их участков, в пределах которых температура поверхности и ее коэффициент излучения считаются постоянными. Суммарная сила излучения

.

Как отмечалось, в общем случае функция распределения энергетической яркости в пространстве предметов многомерная. Однако с точки зрения пространственного распределения (т.е. если исключить распределение яркости по длинам волн и временные флюктуации яркости) эта функция является трехмерной: [2]. Учитывая, что оптические системы приборов пеленгации формируют изображение пространства предметов в фокальной плоскости объектива (удаление до объектов пеленгации значительно больше фокусных расстояний объективов), правомерен переход к двумерной функций распределения яркости в плоскости объекта пеленгации. При решении задачи пространственной фильтрации "точечного" источника с координатами используется математическая модель в виде двумерной функции [9]:

. (1.1)

При пеленгации объектов на дистанциях, при которых угловой размер излучающей поверхности объекта превышает угловое разрешение оптической системы, пользоваться моделью “точечного” источника нельзя. В этом случае наиболее оптимальный вариант - получение экспериментальных данных о распределении яркости по поверхности излучения. Математическое выражение, аппроксимирующее это распределение, может использоваться как математическая модель излучения объекта. При отсутствии экспериментальных данных задаются предполагаемым законом распределения яркости. Например, для объектов с равномерным распределением излучения используется математическая модель, описываемая функцией [8]

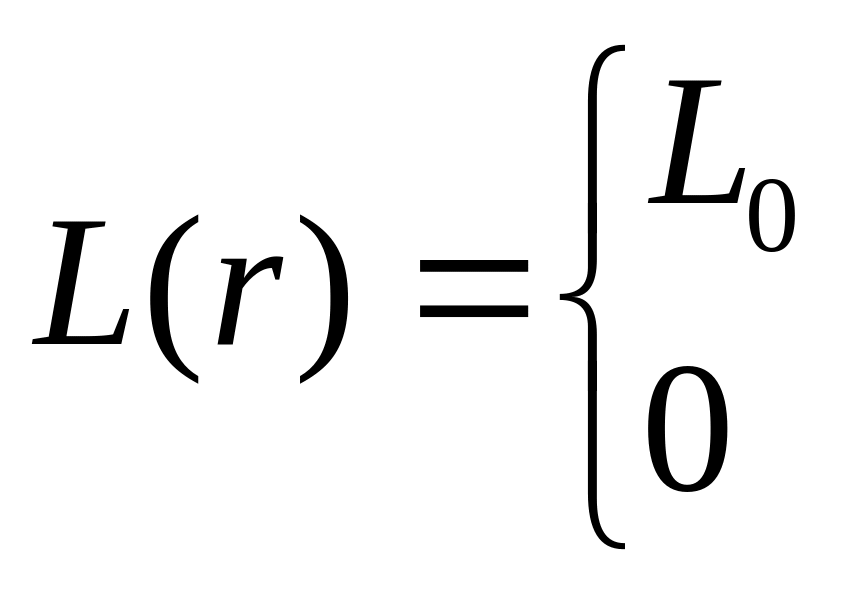
где - область, определяющая объект как излучатель. Для объектов с неравномерным распределением излучения по площади в качестве математической модели распределения энергетической яркости по поверхности используют колоколообразную функцию в полярной системе координат с различным значением “эффективного” радиуса объекта. Для таких объектов

,

где - “эффективный” радиус объекта как излучателя (внутри заключено 63% всего излучения).