2. Применение наращения, дисконтирования и учета в финансовых и коммерческих расчетах.

Предприятие имеет возможность размещать свободные денежные средства на условиях платежеспособности, возвратности и срочности. С целью: получения дохода и сохранения денежных средств от инфляционного обесценения. PV – первоначально размещаемая, исходная сумма денежных средств; r – доход в %-ом выражении; n – единичный промежуток начисления доходов, стандартный интервал; FV – возвращаемая сумма или сумма погашения.

В зависимости от того, какие заданы характеристики изменяется направление движения заданных потоков. Если мы приводим все к концу процесса – это наращение. Если к началу – это дисконтирование.Возвращаемая сумма (FV) – наращенная сумма: PV + PV∙r = FV.

Процесс инвестирования, в котором заданыFV и процентная ставка – дисконтированный процесс. Тогда инвестируемая сумма называется приведенной суммой.

Мультиплицирующий множитель (FM₁(n₁r)) показывает во сколько раз увеличится сумма, вложенная на m-лет под m-процентов годовых.

FM₁(n₁r) = (1+r)^mи FM₂(n₂r) = 1/(1+r)^m

Различают точные и обыкновенные процентные ставки. Точные проценты рассчитываются, исходя из точного количества дней. Приближенные – исходя из приближенного количества дней.

Наращение и дисконтирование может осуществляться по схеме простых и сложных процентов. По формуле простых процентов: инвестируемая сумма ежегодно изменяется на одну и ту же величину – PV∙r.Формула сложных процентов означает, что очередной годовой доход исчисляется не с исходной величины инвестируемого капитала, а с суммы, включающей также ранее начисленные и невостребованные проценты: FV = PV(1+r)^m.

Нужно иметь ввиду, что при одном и том же значении процентной ставки темпы наращения сложных процентов выше темпов наращения простых, если период наращения превышает стандартный интервал начисления дохода. Темпы наращения сложных процентов будут меньше темпов наращения простых процентов, если период наращения меньше стандартного интервала начисления доходов.

В связи с этим областью применения простых процентов являются краткосрочные операции (до 1 года) и с однократным начислением процентов. При краткосрочных операциях используется промежуточная процентная ставка. Это годовая процентная ставка, приведенная к вложению средств: f = t/T, где T – величина стандартного интервала.

Областью применения сложных процентов являются долгосрочные операции (больше 1 года), в том числе предполагающие годовое начисление процентов.Под внутригодовым начислением процентов понимается выплата процентного дохода более 1 раза в год.

Количество выплат доходов – m.

m = 2 называется полугодовым, m = 4 – поквартальным, m = 12 – ежемесячным, m = ∞ – непрерывным.В случае непрерывной выплаты:

При одинаковой величине исходной суммы, одинаковом сроке вложения денежных средств и значения процентной ставки, возвращаемая сумма будет больше в случае использования внутригодовых начислений больше, чем

Процентная ставка, отражающая фактический доход получила название эффективной.Для каждой номинальной процентной ставки нужно рассчитать эффективную процентную ставку: (1+r_e) = FV/PV, где r_e – эффективная процентная ставка.

Если использовать внутригодовые отчисления, то:

Сама эффективная ставка:

Величина r_e зависит от количества внутригодовых отчислений.

Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых составляет дробное количество лет. При этом начисление процентов может осуществляться двумя способами:

1. Начисление процентов с дробным числом лет:

2. Начисление процентов на смешанной основе:

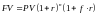
Норма доходности не является постоянной величиной и зависит от риска, связанным с вложением денежных средств.

Темпы инфляции: , где Sp – сумма денег, показательная способность с учетом инфляции равна показательной способности без учета инфляции; So – сумма денег, для которой показательная способность рассматривается без инфляции.

Sp = So(1+r_p); Ip = (1+r_p), где Ip – индекс инфляции.

1. Схема простых процентов:

Пусть r_p равен за период n-лет. Тогда возвращаемая сумма: или

, где r_m – денежная ставка:

Если m=1, то - это формула Фишера. - это инфляционная премия; - это ежемесячный уровень инфляции (темп инфляции).Можно получить r через r_m:

2. Схема сложных процентов:

Если выразить r: .
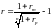