7. Отношения между понятиями

КРУГ ЭЙЛЕРА

Отношения между понятиями. Логические операции с понятиями

      Отношения между понятиями отражают в кругах Эйлера, где каждый круг обозначает объем понятия, а каждая точка – предмет, входящий в объем понятия.       1.  Равнозначныминазывают такие понятия, содержания которых соответствуют друг другу, а объемы совпадают. Например, «великая русская река» и «Волга». X – Волга; R – великая русская река. (рис. 2)

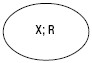
         Рис. 2        2. В отношении пересечениянаходятся понятия, объем одного из которых частично входит в объем другого понятия. Например, «юрист» и «военнослужащий». X – юрист; R – военнослужащий. (рис. 3)

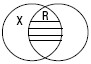
         Рис. 3        В совместившейся части круга х и R (заштрихованная часть) мыслятся те юристы, которые являются военнослужащими.       3. В отношении подчинениянаходятся понятия, объем одного из которых полностью входит в объем другого, составляя его часть. Например, «преступление» и «взятка». X – преступление; R – взятка.(рис. 4)

        Рис. 4       Понятие, имеющее больший объем и включающее объем другого понятия, называется подчиняющим. Понятие, имеющее меньший объем и составляющее часть объема другого понятия, – подчиненным. Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родом, а подчиненное – видом.       Если в отношении подчинения находятся общее и единичное понятие, то общее называют видом, а единичное – индивидом. Понятия, объемы которых не совпадают ни полностью, ни частично, называются несовместимыми.       Существуют три вида несовместимости: соподчинение, противоположность, противоречие.       1. В отношении соподчинениянаходятся два или более неперекрещивающихся понятия, подчиненных общему для них понятию.       Например, «следователь», «адвокат» и «юрист». Z – юрист; У – следователь; X – адвокат. (рис. 5)

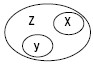
         Рис. 5        2. В отношении противоположностинаходятся понятия, одно из которых содержит некоторые признаки, а другое эти признаки отрицает, заменяя их на противоположные. Например, «черный» и «белый». Z – черный; Р – белый. (рис. 6)

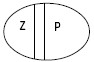
         Рис. 6        3. В отношении противоречиянаходятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает, не замещая их никакими другими признаками. В отношении противоречия находятся отрицательные и положительные понятия.

По содержанию между понятиями могут быть только два вида отношений - сравнимость и несравнимость. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (романс и кирпич). Между ними невозможны логические отношения.

Сравнимые понятия - это понятия, имеющие в своем содержании общие, существенные признаки (по которым они и сравниваются). Напр., право и мораль. Отношения между понятиями изображают с помощью схем - кругов Эйлера. Между сравнимыми понятиями возможны два вида отношений по объему: совместимость и несовместимость.

Совместимые понятия - это такие, объемы которых полностью или частично совпадают. Между совместимыми понятиями складываются следующие отношения:

1 - равнообъемность. Равнообъемными или равнозначными называются понятия, которые различаются по своему содержанию, но объемы которых совпадают. Напр., "Л.Н. Толстой" - А и "автор романа "Война и мир" - В. Объемы тождественных понятий изображаются кругами, полностью совпадающими.

2 - перекрещивание. Перекрещивающимися называются понятия, объемы которых частично совпадают, напр. "студент" и "спортсмен", "юрист" и "писатель". Они изображаются пересекающимися кругами. В перекрещивающейся части двух кругов мыслятся студенты, являющиеся спортсменами. В левой части круга мыслятся студенты, не являющиеся спортсменами, а в правой части - спортсмены, не являющиеся студентами.

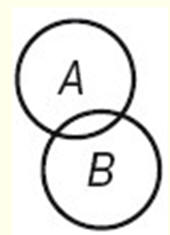
3 - подчинение. В отношении подчинения (субординации) находятся понятия, если объем одного полностью входит в объем другого, но не исчерпывает его. Это отношение вида - В и рода - А (млекопитающее и кошка).

Несовместимыми называются понятия, объемы которых не совпадают. Несовместимые понятия могут находиться между собой в следующих отношениях.

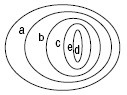
1 - соподчинение. В отношении соподчинения (координации) находятся понятия, объемы которых исключают друг друга, но принадлежат некоторому более общему родовому понятию. Напр., "ель" - B, "береза" - C принадлежат объему понятия "дерево" - А. Они изображаются неперекрещивающимися кругами внутри общего круга. Это виды одного и того же рода.

2 - противоположность. В отношении противоположности (контрарности) находятся два понятия, признаки которых противоречат друг другу, а сумма их объемов не исчерпывает родового понятия (храбрость - трусость).

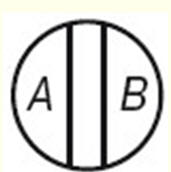
3 - противоречие. В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя никакими другими (напр., А - белая краска, тогда понятие, находящееся с ним в отношениях противоречия, следует обозначить не-А (не белая краска). Круг Эйлера в этом случае делится пополам и между ними нет никакого третьего понятия.