5. Эллипсоид.

Поверхность, определяемая уравнением

. (15)

Называется эллипсоидом. Числа а, b и с называются полуосями эллип­соида. Так как в уравнение (15) текущие координаты входят в чет­ных степенях, то эллипсоид симметричен относительно координатных плоскостей. Чтобы установить форму эллипсоида, будем пересекать его плоскостями, параллельными координатным плоскостям. Покажем, что если пересечь эллипсоид плоскостью z = h (| h | < с), то в сечении получится эллипс L. В самом деле, исключая из уравнений

аппликату z, получим уравнение цилиндрической поверхности, проектирующей сечение L на пло­скость Оху:

, или

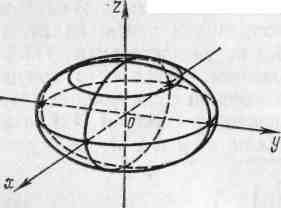
Рис..7.

Из этого уравнения видно, что кривая L есть эллипс с полуосями

, . (16)

Из формул (16) видно, что с возрастанием |h| полуоси эллипса а и b уменьшаются. При |h|=c имеем , и сечение вырождается в точку. При |h|>с эллипсоид с плоскостью z = h, очевидно, не пересекается. Аналогично можно показать, что при пересечении эллипсоида плоскостями х = h (| h | < а и y = h (| h | < b ) также получатся эллипсы. Эллипсоид имеет вид, изображенный на рис. 7. В частном случае при а = b получаем эллипсоид вращения

. (17)

Если все три полуоси равны между собой, с = b = а, то получится сфера + y² + z² = а².

6. Гиперболоиды.

Поверхность, определяемая уравнением

. (18)

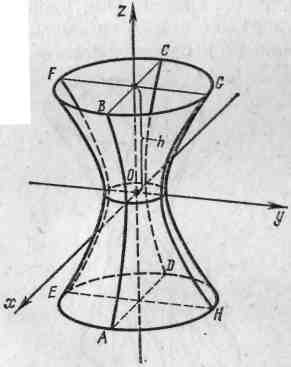
называется однополостным гиперболоидом. Эта поверхность имеет три плоскости симметрии - координатные плоскости, так как текущие координаты х, у и z входят в уравнение (18) в четных степенях. Пересекая однополостный гиперболоид плоскостью у = 0, получим лежащую в плоскости Oxz гиперболу ABCD (рис. 8)

Аналогично, в сечении однополостного гиперболоида плоскостью х = 0 получится гипербола EFGH

лежащая в плоскости Oyz.

При пересечении однополостного гиперболоида плоскостью z = h получится эллипс BFCG, уравнения которого имеют вид: или

.

Рис. 8

Полуоси этого эллипса и возрастают с возрастанием абсолютной величины h . При h = 0 получится эллипс, лежащий в плоскости Оху и имеющий наименьшие полуоси а и b.

При а = b получим однополостный гиперболоид

. (19)

При пересечении его плоскостями z = h получаются окружности

В п. 2 и 3 рассматривались цилиндрические и конические поверхности каждая из которых составлена из прямых. Оказывается, однополостный гиперболоид можно также рассматривать как поверхность, составленную из прямых линий. Рассмотрим прямую, определяемую уравнениями:

(20)

в которых а, b и с - полуоси однополостного гиперболоида, а - произвольно выбранное число ( ).

Перемножив левые и правые части этих уравнений, получим :

, или ,

т. е. получим уравнение однополостного гиперболоида.

Таким образом, уравнение однополостного гиперболоида является следствием системы уравнений (20). Поэтому координаты любой точки М (х; у; z), удовлетворяющие системе (20), удовлетворяют также и уравнению (18) однополостного гиперболоида. Иными словами, все точки прямой (20) принадлежат гиперболоиду (18). Меняя значения k, мы получим целое семейство прямых, лежащих на поверхности (18). Аналогично можно показать, что однополостному гиперболоиду принадлежат все прямые семейства:

(21)

Где l — произвольный параметр.

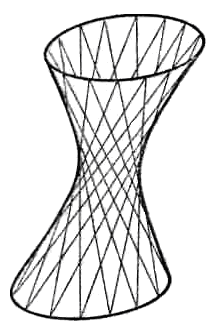
Рис. 9

Можно также показать, что через каждую точку однополостного гиперболоида проходит по одной прямой каждого из указанных семейств. Таким образом, однополостный гиперболоид можно рассматривать как поверхность, составленную из прямых линий (рис. 9). Эти прямые называются прямолинейными образующими однополостного гиперболоида.

Возможность составления поверхности однополостного гиперболоида из прямых линий используется в строительной технике. Так, например, по конструкции, предложенной инженером Шуховым , в Москве была сооружена радиомачта с помощью балок, расположенных по прямолинейным образующим однополостного гиперболоида.

Поверхность, определяемая уравнением

, (22)

называется двуполостным гиперболоидом.

Координатные плоскости являются плоскостями симметрии для двуполостного гиперболоида. Пересекая эту поверхность координатными плоскостями Oxz и Оуz, получим соответственно гиперболы

и 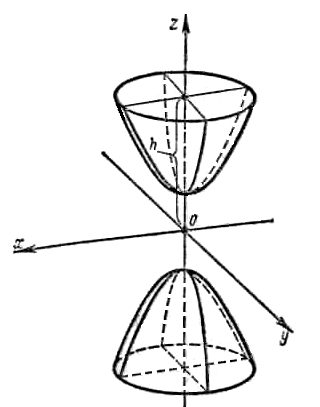Рис.10

Если двуполостный гиперболоид пересечь плоскостью

z = h (при | h |>c ), то в сечении получится эллипс

с полуосями

и ,

возрастающими при возрастании | h |. При | h |<с поверхность (22) с плоскостью z = h, очевидно, не пересекается. Двуполостный гиперболоид состоит из двух отдельных частей (полостей), чем и объясняется его название. При а = b уравнение (22) имеет вид

или . (23)

и является уравнением двуполостного гиперболоида вращения. В сечении последнего с плоскостью z = h (| h |>c) получится окружность

радиуса R= .