§ 7 Полярная система координат.

Полярная система координат на плоскости определяется за- данием некоторой точки , называемой полюсом; исходящего из этой точки луча , называемого полярной осью и мас -штабной единицей для измерения длин.

Для произвольной точки плоскости координатами в дан- ной системе координат называют полярный радиус , вычисленный в масштабных единицах, и полярный угол между осью и радиус – вектором , т.е. ,

1

Чаще всего предполагают, что или Иногда допускаются отрицательные значения для , но при этом соответствующие значения откладываются на продолжении луча.

Установим связь между полярными координатами точки и её декартовыми координатами. Для этого совместим начало декартовой системы координат с полюсом полярной системы координат, а ось - с полярной осью:

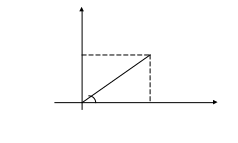
Используя тригонометрические формуды легко получаются формулы перехода от декартовых координат к полярным:

(1)

и формулы обратного перехода от полярных координат к де- картовым:

(2)

Чаще всего эти формулы используются комбминированно.

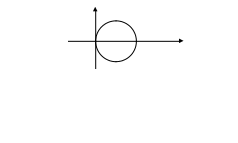
Окружность в полярной системе координат имеет уравнение , или , тогда дпнная линия имеет вид:

Аналогичным образом, окружность имеет в полярных координатах уравнение и соответству- ющий рисунок линии выглядит следующим образои:

Окружность с центром в начале координат в полярных координатах имеет уравнение или .

Если задано уравнение линии в полярных координатах , то чтобы построить данную линию в полярной сис- теме координат, заполняют таблицу значений этой функции в точках, вычисленных для значений аргумента , причём, чем больше , тем точнее будет построение линии.

Пример 1. Построить линию: .

Заполнить таблицу значений данной функции:

	0
	2	3	2	1	2	3	2	1	2

	3	2	1	2	3	2	1	2

Построим данную линию

При построении линии в полярных координатах можно по -ступать и иначе, а именно, используя свойства соответствую- щих функций.

Пример 2. Пусть дано уравнеие . Так как , то максимальное значение данная функция принимает при - ; мини –мальное значение будет в точке - .

Так как чётная функция, то также чётная функция и поэтому соответствующая линия симме- трична отностьельно полярной оси. Таким образом, получаем линию:

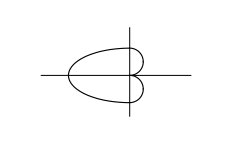
Эту линию называют кардиоидой, имея ввиду её форму.

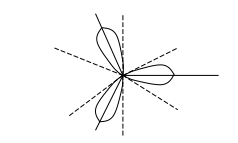
Пример 3. Построить линию .

Достаточно построить данную линию на промежутке , так как период данной функции равен . Учитывая, что в промежутке , следовательно . После этого, учитывая периодичность функции, можно построить ещё две части этой линии, которые получаются при .

0

В заключение параграфа напишем уравнение эллипса, ги - перболы и параболы в полярных координатах.

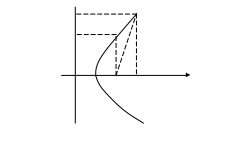Пусть - дуга эллипса, гиперболы или параболы:

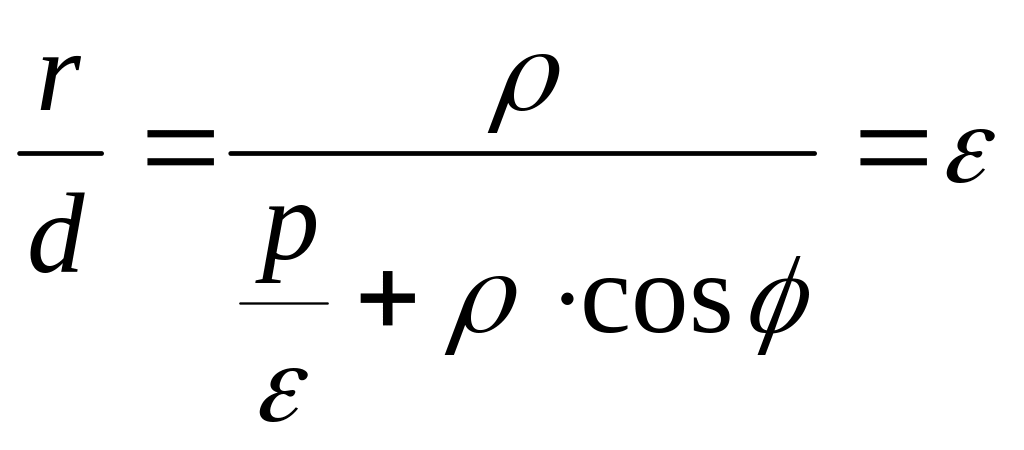Совместим фокус с полюсом, а ось симметрии - с по- лярной осью. Точка выбрана так, что . По свойству директрисы: . Пусть , или . Для точки имеем . Тогда, . Обозначив , получим . Сле- довательно, , отсюда: , или . Окончательно получаем уравнение:

. (3)

При - это уравнение эллипса; при - это уравнение одной ветки гиперболы; при - это урав – нение параболы.

Пример 4. Построить линию и записать её уравнение в декартовой системе координат.

Можно произвести построение данной линии непосред- ственно в полярной системе координат, как в примере 1. Но в данном случае, учитывая формулу (3), это уравне -ние эллипса с . Поэтому более удобно сначала перейти к декартовым координатам и только после этого построить линию (менее трудоёмкий вариант решения). Преобразуем уравнение линии: . Исполь –зуя формулы (1) и (2), получаем:

(4) обе части полученного равенства возведём в квадрат:

Получено каноническое кравнение эллипса:

Его центр симметрии , полуоси

П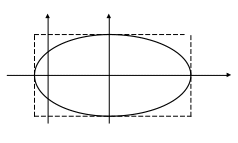 остроим данную линию:

3

4 5

Уравнение вида такжа определяет линию 2 – го порядка, но в этом случае сдвиг точки происходит вле- во, а уравнение приводит к смещению линии по оси .