МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Г.И. НОСОВА

Л.А. ИЗОСОВА

А.В.ИЗОСОВ

Л.А. ГРАЧЁВА

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ, ВЕКТОРНОЙ

АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Утверждено Редакционно – издательским советом университета

в качестве учебного пособия

МАГНИТОГОРСК

2008

УДК 519.6

Рецензенты

Изосова Л.А., Изосов А.В., Л.А. Грачёва

Элементы линейной алгебры, векторной алгебры и аналити ческой геометрии: Учеб. пособие. - Магнитогорск: МГТУ, 2008

Глава 1. Элементы линейной алгебры

§ 1. Матрицы и алгебраические действия с ними.

Определение. Матрицей называется прямоугольная табли –ца состоящая из строк и столбцов, заполненная либо числами, либо некоторыми символами, при этом говорят, что она имеет размерность . Общий вид матрицы можем представить следующим образом:

,

или, в более компактном виде:

Если , т.е. матрица размерности , то матрицу на- зывают вектор – столбцом, если , т.е. матрица размер -ности , то её называют вектор – строкой. Матрица, у ко- торой все элементы равны нулю, называется нулевой. Матри -ца, у которой число строк равно числу столбцов назы – ется квадратной матрицей порядка .

Элементы образуют главную диагональ квад- ратной матрицы. Если равны нулю все элементы квадратной матрицы, кроме элементов главной диагонали, которые не все равны нулю, то матрица называется диагональной порядка . Если все элементы главной диагонали диагональной матрицы равны между собой, то она называется скалярной. Диагональ- ная матрица, все диагональные элементы которой равны 1, называпется единичной. Если все элементы квадратной матри- цы, расположенные выше (или ниже) главной диагонали равны нулю, то матрица называется треугольной. Приведём приме -ры перечисленных матриц:

1. Вектор – столбец размерности :

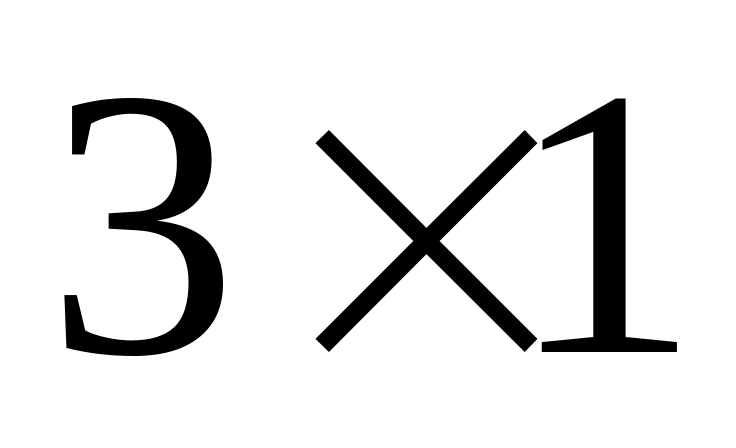2. Вектор – строка размерности : :

3. Нулевая матрица размерности

4. Квадратная матрица порядка 3:

5. Диагональная матрица четвёртого порядка:

5. Скалярная матрица второго порядка :

5. Единичная матрица третьего порядка:

5. Треугольные матрицы:

Две матрицы и называют- ся равными, если они имеют одинаковые размерности и совпадают элементы с одинаковыми индексами (т.е. совпа- дают элементы, расположенные на одинаковых местах):

В этом случае пишут .

АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С МАТРИЦАМИ

1. Умножение матрицы на число.: возможно для матриц лю-

бой размерности. При умножении матрицы на число каждый элемент матрицы умножается на это число, т.е.

,

Например, если , то .

2. Алгебраическое сложение матриц (т.е. сложение и вычи- тание) можно выполнять только для матриц одинаковой раз –мерности и производится поэлементно, т.е., если даны две матрицы и , то

Например, если , , то

;

.

3. Умножение матриц возможно только в том случае, ес- ли число столбцов первой матрицы равно числу строк вто- рой матрицы. В результате умножения получается матрица, у которой число строк равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.

Замечание. Согласно этому правилу, умножение матриц возможно далеко не всегда. Кроме того, даже если умножение матриц возможно, нельзя менять их местами при умножении, так как это может привести к совершенно различным резуль- татам.

Таким образом, если , а , т.е. в матрице столбцов, а в матрице строк, то после умножения получится матрица , где элемент равен сумме произведений соответствующих элементов -й строки матрицы и -го столбца матрицы , т.е.

,

где .

Чтобы понятнее был способ умножения матриц, рассмотрим следующий пример 1:

.

Ещё один пример 2 умножения числовых матриц:

Перемножим эти же матрицы в другом порядке:

Умножение этих матриц также было возможно, но в резуль- тате умножения получили совершенно другую матрицу, более того, даже матрицу другой размерности.

Матрицы же, рассмотренные в примере 1, вообще нельзя перемножить в другом порядке, так как у второй матрицы 2 столбца, а у первой матрицы 3 строки и, согласно правилу умножения, умножение таких матриц невозможно. Поэтому ум- ножение матриц антикоммутативно, т.е., в общем случае,

Деление для матриц не определяется, но можно для неко- торых матриц ввести понятие обратной матрицы (только для квадратных невырожденных матриц).

Определение. Матрица называется обратной к матри- це , если выполняется равенство:

,

где - единичная матрица.

В завершение параграфа отметим следующие свойства алгебраических действий с матрицами.

Пусть - некоторые матрицы, - числа. Тогда можно легко убедиться в справедливости следующих равенств:

1) (коммутативность сложения);

2) (ассоциативность сложения);

3) Для любой матрицы размерности существует нулевая матрица той же размерности, такая что выполнено:

4) Для любой матрицы существует противоположная мат- рица , такая что

5) для любой матрицы

6)

7)

8)

9) , если умножение возможно (ассо -циативность умножения);

10) , если все эти операции воз -можны (дистрибутивность умножения);

11) (антикоммутативность);

12) Для любой невырожденной квадратной матрицы су -ществует обратная матрица, такая что .