1. Экономико-математические модели.

Математическое программирование - это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.

Прежде чем применять математические методы для решения задач экономики, необходимо выразить экономическое содержание задачи через определенные математические зависимости, т.е. составить экономико-математическую модель задачи.

Рассмотрим задачу об использовании ресурсов.

Предположим, что предприятие выпускает

n различных изделий. Для их производства требуется m различных видов ресурсов (разных видов сырья, вспомогательных материалов, запасов машинного времени, людских ресурсов и т.д.). Эти ресурсы ограничены и составляют в планируемый период соответственно b₁, b₂ b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы j-го вида изделий (i = 1, 2, ..., m; j = 1, 2, ..., n) . Пусть прибыль, получаемая предприятием при реализации единицы изделия j-гo вида равна C_j. В планируемый период все показатели а_ij, с_j, b_i предполагаются постоянными.

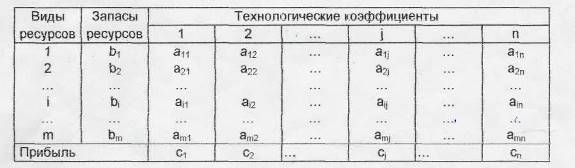
Допустим, что предприятие будет выпускать x₁ единиц

изделий 1-го вида, х₂ единиц изделий 2-го вида, ...,

х_n единиц изделий n—го вида. Должны выполняться ограничения:

Т ребуется составить такой план выпуска продукции, при котором прибыль предприятия от реализации ее была бы наибольшей.

причем х₁, х_2, ..., х_n должны быть неотрицательны.

Система линейных неравенств вместе с условием неотрицательности переменных составляют систему ограничений данной задачи по объему соответствующего ресурса, т.к. в ходе выполнения плана можно использовать либо весь запас этого ресурса, либо часть его.

Требуется составить оптимальный план работы предприятия х = (x₁; х₂; . . . ; х_n), т.е. найти такие неотрицательные значения xl, х2, ..., хn, которые бы удовлетворяли системе ограничений и при которых прибыль от реализации всей продукции

F = была бы максимальной.

Определение:

Функцию F, которая выражает конечную цель оптимального планирования, называют целевой.

В данном случае функция выражает получение наибольшей прибыли.

Эта функция является линейной.

Общая задача линейного программирования

В общем случае задача линейного программирования сводится к отысканию такого решения х = (x₁; х₂; ...; х_n) системы m линейных уравнений с n переменными

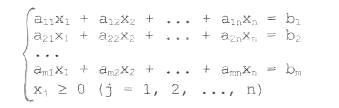
при котором целевая функция F = + с₂х₂ + ... + с_nх_n принимает оптимальное (максимальное или минимальное) значение.

Решение х = (х₁; х₂; ...; х_n) при котором функция F обращается в оптимум, называется оптимальным решением.

В задачах линейного программирования коэффициенты - заданные постоянные величины, а число уравнений меньше числа переменных, т.е. m<n.

Все правые части системы неотрицательны, т.е. b_j (i = 1, 2, ..., m). Если в некоторых уравнениях системы это условие нарушено, то можно умножить обе части таких уравнений на -1.

Задача линейного программирования, система ограничений которой задана в виде системы уравнений, носит название канонической.

Задачу можно записать в более короткой форме; найти решение

х = (х₁, х₂, ..., х_n) системы ограничений

(i = 1, 2, ..., m) приводящее к оптимуму линейную функцию , при

условии, что хj ≥ 0 (j = 1, 2, . . ., n) .

Для записи системы часто употребляется векторно-матричная форма:

AX = В матрица А - матрица условий задачи.

В = (b₁, b₂, ..., b_m) - вектор ограничений.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, причем возможны различные формы таких систем:

(i = 1, m) или

или смешанные ограничения (≥; ≤).

Но любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (отнять) какое-либо неотрицательное число - добавочную переменную, с тем, чтобы каждое неравенство обратилось в уравнение.

Таким образом как бы не были первоначально заданы ограничения задачи линейного программирования, их всегда можно привести к системе линейных уравнений, т.е. свести задачу к канонической.

Система m-линейных уравнений с n-переменными может быть совместной и несовместной; уравнения системы - зависимы и независимы,

Несовместность системы означает, что ее уравнения противоречивы. Система не имеет решения => не имеет решения задача линейного программирования.

Будем считать, что все m-уравнений системы линейно-независимы. В противном случае можно исключить часть уравнений так, чтобы уравнения системы стали линейно независимыми.

Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и (n-m) неосновных (свободных) переменных. Неосновные переменные в базисном решении равны нулю.

Если хотя бы одна из основных переменных принимает нулевое значение, то соответствующее базисное решение называется вырожденным.

Т.к. компоненты оптимального решения задачи линейного программирования не могут быть отрицательными, то поиски этого решения нужно ограничить только допустимыми решениями системы ограничений.