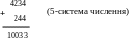5. Переведення 16-чисел 2-числа і навпаки

Нехай задане S-число

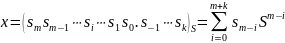
і основа системи числення є ступенем 2:

,

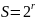де 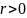 – ціле число. Тоді

і, враховуючи що

,

( ),

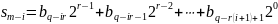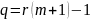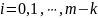а числа 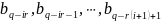дорівнюють 0 або 1, маємо

=

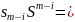
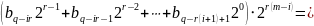
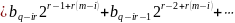
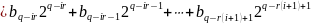
і число

.

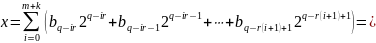
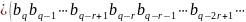
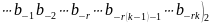Порівнявши результати з

.

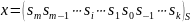зробимо висновок, що для переведення S-числа у 2-число досить зробити заміну кожної цифри її -розрядним двійковим еквівалентом:

.

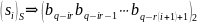У випадку 16-системи числення і кожну 16-цифру необхідно замінити 4-розрядним двійковим еквівалентом (табл. 2.1).

Приклад 1.

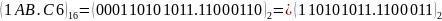
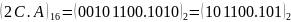
Для переведення 2-числа в 16-число необхідно розбити його на четвірки справа наліво і кожну таку четвірку замінити 16-цифрою (застосовуючи табл. 2.1). Якщо не вистачає цифр, то необхідно додати нулі зліва в цілій частині й справа – у дробовій.

Приклад 2.

.

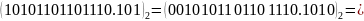
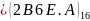
Просте правило переведення 2-чисел у 16-числа, і навпаки можна застосувати для переведення великих 10-чисел у двійкові. Необхідно 10-число спочатку перетворити на 16-число, а потім 16-число –  у 2-число. Це значно скорочує кількість необхідних операцій ділення і множення.

Приклад 3. .

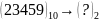Розв’язання.

.

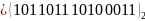Вправа 1. Перевести:

• ;

• ;

• ;

• 

• ;

• .

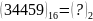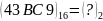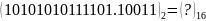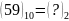
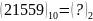Вправа 2. Перевести:

• ;

• ;

• ;

• ;

• ;

• .

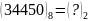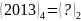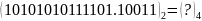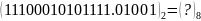6. Додавання і віднімання в s-системі числення

Додавання і віднімання чисел у S-системі числення здійснюється за правилами 10-системи числення. При цьому можна скористатися відповідними таблицями додавання. Вони легко складаються самостійно.

Приклад 1. Для 6-системи числення ця таблиця має вигляд

+	1	2	3	4	5
1	2	3	4	5	10
2	3	4	5	10	11
3	4	5	10	11	12
4	5	10	11	12	13
5	10	11	12	13	14

Приклад 2. Застосовуючи таблицю з прикладу 1, додати 6-числа _.

Розв’язання. Дія додавання виконується в “стовпчик”:

Додаємо в 0-розряді 5+4=13, 3 пишемо в 0-розряді, 1 переносимо в 1-розряд. Додаємо в 1-розряді 1+4=5, 5+3=12, 2 пишемо в 1-розряді, 1 переносимо в 2-розряд. Додаємо у 2-розряді 1+3=4, 4+2=10, 0 пишемо, 1 переносимо в 3-розряд. Додаємо в 3-розряді 1+1=2.

Отже,

Приклад 3. Необхідно додати два числа .

Розв’язання.

Приклад 4. Необхідно відняти два числа .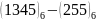

Розв’язання. Дія віднімання виконується в “стовпчик”:

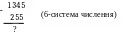
Віднімаємо в 0-розряді 5-5=0. Віднімати в 1-розряді не можна, необхідно “позичити” одну одиницю. Маємо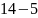 . У рядку таблиці, яка відповідає 5, знаходимо 14 і за номером стовпчика з 14 робимо висновок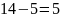 . Віднімаємо у 2-розряді 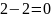і, нарешті, зносимо 1 в 3-розряді. Отже,

Приклад 5. _.

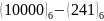У цьому прикладі “позичати” одиницю довелося в 4-розряді: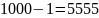 . Тому в 3,2,1-розрядах “розсипалися” 5.

Приклад 6. _.

Розв’язання.

Виконувати дії додавання і віднімання за таблицями не зовсім зручно. Зручніше виконувати ці дії методом порозрядного переведення в 10-систему числення, суть якого має бути зрозуміла із прикладів.

Приклад 7.

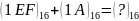
Розв’язання. Додаємо в 0-розряді:

,

9 пишемо в 0-розряді, а 1 переносимо в 1-розряд.

Додаємо в 1-розряді:

1+Е=F, F+1=10,

(тут дії виконалися без переведення в 10-систему), 0 пишемо, 1 переносимо в 2-розряд.

Додаємо у 2-розряді:

1+1=2.

Отже,

11

(16-система числення)

1EF

+

1A

209

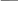
Приклад 8. .

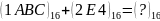Розв’язання.

0-розряд:

,

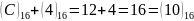0 пишемо, а 1 переносимо.

1-розряд:

,

,

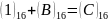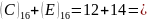
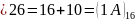А пишемо, 1 переносимо.

2-розряд:

, .

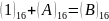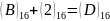3- розряд: 1 зносимо.

Отже,

11

1ABC

(16-система числення)

+

2E4

1DA0

Приклад 9. .

Розв’язання.

0-розряд:

.

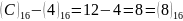1-розряд: позичаємо 1 у 2-розряді,

.

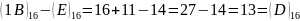2-розряд:

, .

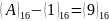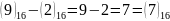3-розряд: 1 зносимо.

-

1ABC

(16-система числення)

2E4

17D8

Приклад 10. .

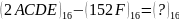Розв’язання

0-розряд: позичаємо 1 в 1-розряді,

.

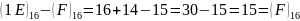1-розряд:

, .

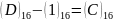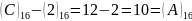2-розряд:

.

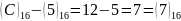3-розряд:

.

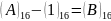4-розряд: 2 зносимо.

Отже,

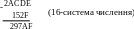
Приклад 11. .

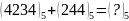Розв’язання

0-розряд:

,

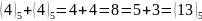3 пишемо, 1 переносимо.

1-розряд:

, ,

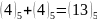3 пишемо, 1 переносимо.

2-розряд:

, ,

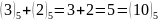0 пишемо, 1 переносимо.

3-розряд:

,

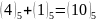0 – пишемо, 1 – переносимо.

4-розряд: зносимо 1.