1. Системи числення

Система числення визначається як система множини символів, що називаються цифрами, та множини правил запису чисел із використанням цих цифр.

Системи числення поділяються на непозиційні, позиційні, змішані.

У непозиційних системах числення значення кожної цифри не залежить від місця, яке вона займає в зображенні числа, у позиційних – залежить. У змішаних системах числення поєднуються характерні властивості позиційних та непозиційних систем числення.

Приклад 1. Прикладом непозиційної системи числення може бути римська нумерація. Так, у числах XIV (чотирнадцять) та XVI (шістнадцять) цифра V позначає п’ять одиниць, незважаючи на те, що займає різні місця в зображенні чисел.

Приклад 2. Прикладом позиційної системи числення є звична десяткова система, яка застосовується у повсякденному житті. Так, у числі 555 цифра 5 має різне значення: перша цифра позначає п’ять сотень, друга –п’ять десятків, третя – п’ять одиниць.

Нагадаємо, що в 10-системі числення запис

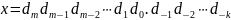
є скорочене позначення числа

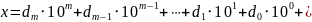
. (1)

Показники степені десятки називаються розрядами числа, а самі степені 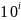визначають вагу i-розряду.

В інформатиці в основному застосовуються позиційні системи числення (змішані системи числення застосовуються в теорії інформації та кодування, при передачі даних тощо, які тут не розглядаються). Тому надалі позиційні системи числення будемо називати просто системами числення.

Кількість цифр системи числення називається основою системи числення. За основою системи числення поділяються: на 2-систему числення із цифрами 0, 1; 3-систему числення із цифрами 0, 1,2; ...; 8-систему числення із цифрами 0, 1, 2, 3, 4, 5, 6, 7; ...; 12-систему числення із цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В; 16-систему числення із цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F і т.д.

В інформатиці застосовуються 2, 8, 10, 16-системи числення. Двійкова система числення застосовується для двійкового кодування даних та команд процесора, 16-система –для скороченого запису двійкових кодів, 8-система для зображення даних у деяких алгоритмічних мовах.

Вправа 1. За допомогою арабських цифр та великих букв латинського алфавіту записати цифри 20, 30-систем числення.

2. Запис цілих чисел із діапазону у різних системах числення

Записи цілих чисел із діапазону у 10,2,8,16-системах числення наведені в таблиці 1. У подальшому запис числа в системі числення з основою S називатимемо S-числом Надалі S-числа записуватимуться в круглих дужках із індексом S: , , 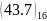. Десяткові числа записуватимуться без круглих дужок та індексу: 45.6, 235, 356.

Таблицю 1 можна застосувати для переведення чисел із однієї системи числення в іншу.

Приклад 1. , , .

.

.

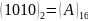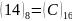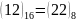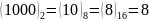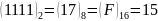Таблиця 1

10 с.ч.	2 с.ч.	16 с.ч.	8 с.ч.	216
0	0	0	0	0000
1	1	1	1	0001
2	10	2	2	0010
3	11	3	3	0011
4	100	4	4	0100
5	101	5	5	0101
6	110	6	6	0110
7	111	7	7	0111
8	1000	8	10	1000
9	1001	9	11	1001
10	1010	А	12	1010
11	1011	В	13	1011
12	1100	С	14	1100
13	1101	D	15	1101
14	1110	Е	16	1110
15	1111	F	17	1111
16	10000	10	20	-
17	10001	11	21	-
18	10010	12	22	-
19	10011	13	23	-
20	10100	14	24	-