Пример на закрепление Графический метод решения задач линейного программирования

Графическим методом можно решать, в основном, задачи линейного программирования, имеющие две переменные.

Решим графическим методом задачу линейного программирования с двумя переменными, изложенную и рассмотренную выше.

Начнём решение задачи с построения области её допустимых решений (рисунок 1). В первую очередь отобразим в прямоугольной системе координат условия неотрицательности переменных (3). В двумерном пространстве уравнению соответствует прямая, а неравенству - полуплоскость, лежащая по одну сторону от прямой. Построим прямые х₁=0, и х₂=0, которые лежат на границах полуплоскостей и совпадают с осями координат. Полуплоскости х1>0, х2>0 лежат соответственно справа от оси Ох₂ и выше оси Ох₁. Множество точек, удовлетворяющих одновременно неравенствам х₁0 и х₂0, представляет собой пересечение построенных полуплоскостей вместе с граничными прямыми и совпадает с точками первой четверти.

Рассмотрим ограничения задачи ,построим по порядку прямые:

6х₁+6х₂=36

4х₁+2х₂=20

4х₁+8х₂=40

и определим, с какой стороны от этих прямых лежат полуплоскости, точки которых удовлетворяют соответственно строгим неравенствам:

6х₁+6х₂≤36

4х₁+2х₂≤20

4х₁+8х₂≤40

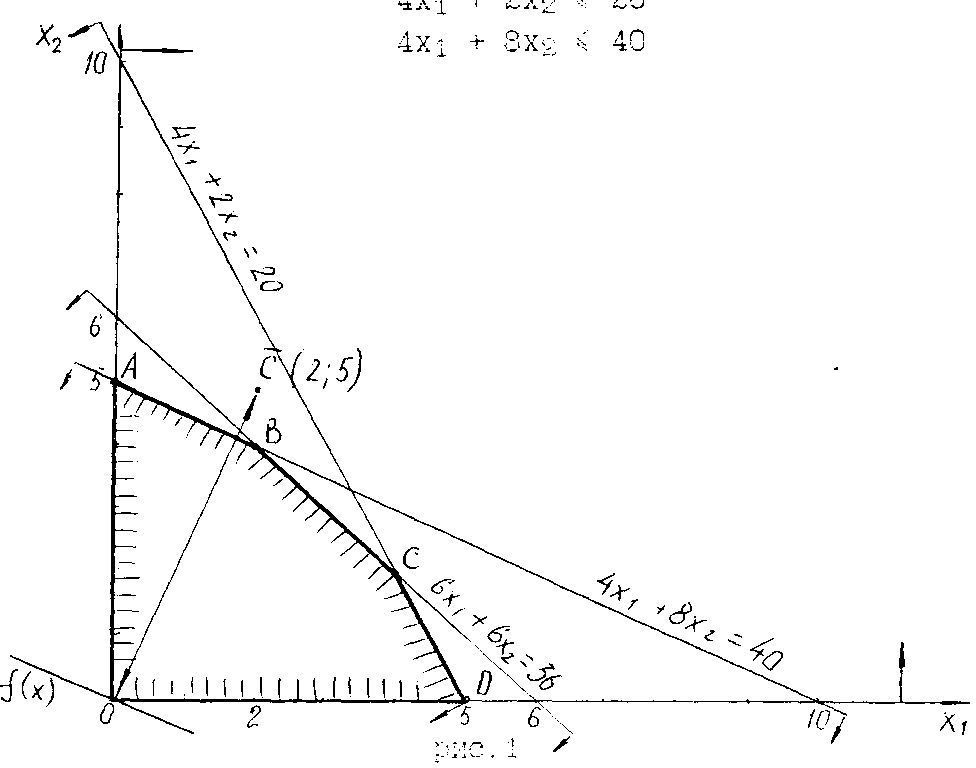
Рисунок 1

Сторона, в которой располагается полуплоскость от прямой, указывается стрелками. Существует следующий способ определения полуплоскости: если коэффициент при х₂ в ограничении положительный, то неравенству «>» соответствует полуплоскость, лежащая выше граничной прямой, а неравенству «<» - полуплоскость, лежащая ниже граничной прямой. Если коэффициент при х₂ в ограничении отрицательный, то наоборот.

Область определения задачи (1)-(3) будет представлять собой пересечение всех построенных полуплоскостей. В данном случае это многоугольник ABCDO, каждая точка которого, включая и точки, лежащие на его границах, будет удовлетворять ограничениям (2) – (3).

Следующим этапом присвоим функции f значение нуль и построим прямую

2х₁+5х₂=0 (9)

Эта прямая проходит через начало координат. В левой части уравнения (4) стоит скалярное произведение двух векторов

= (С₁;С₂) = (2;5) и = (х₁;х₂) (10).

Если скалярное произведение векторов равно нулю, то векторы перпендикулярны.

Построим вектор [он проходит через начало координат и точку (2;5)] и перпендикулярно ему через начало координат проведём прямую (4).

Вектор всегда показывает направление возрастания значения целевой функции, а противоположный ему вектор (- ) – направление убывания значения целевой функции. Передвигая прямую (4) по области определения параллельно самой себе в направлении вектора , значение целевой функции будет возрастать, и наоборот, передвижение в направлении вектора (- ) даёт убывание значения целевой функции.

Как видно из рис1, целевая функция f в задаче (1)-(3) достигает своего максимального значения в точке А многоугольника, а минимального – в точке 0.

Оптимальному решению задачи (1) – (3) соответствует точка А, которая лежит на пересечении прямых

X₂=0 (11)

4х₁+8х₂=40

Для определения координат точки А решим систему (7). В результате получим: х₁=0, х₂=5, f_max=2*0+5*5=25.

15