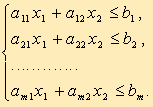Технологическая карта (план) занятия № 7

Дисциплина Математические методы

Тема Использование графического метода решения злп с двумя переменными. Решение злп графическим методом.

Тип занятия Изучение и закрепление нового материала

Вид, форма занятия Комбинированный урок

Цели урока:

• внести вклад в математическое воспитание;

• алгоритмическую культуру;

• развивать умение рационально выбирать решение специальных задач;

• развивать умение применять на уроках знания полученные при изучении другой дисциплины;

• сформировать связь между теорией и практикой;

• закрепить знания, умения, навыки, новый материал;

• обращать внимание учащихся на записи и рациональные приемы решения в тетради, на оформление решения в математических приложениях;

• формирование умений и навыков самообразования

Литература:

• Патыка Т.Л., Попов И.И. Математические методы: Учебник, 2005.

• http://matmetod-popova.narod.ru

• http://ru.wikipedia.org

• Агальцов В.П., Волдайская И.В. Математические методы в программировании: Учебник, 2006

• Данко П.Е. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1997, 1 часть

Требования к урокам:

Студент должен:

Знать:

• алгоритм графического решения ЗЛП;

• понятие целевой функции и системы ограничений;

Уметь:

• находить область допустимых значений системы неравенств графическим способом

Содержание урока:

1. Организационный момент проверка посещаемости, постановка целей урока

2. Повторение материала - проверочная письменная работа по домашнему заданию - приведение к канонической форме задач линейного программирования (10 вариантов).

3. Изучение нового материала

3.1 Геометрическое истолкование задачи в стандартной форме в случае двух переменных.

3.2 Алгоритм графического метода решения задач ЛП

3.3 Решение задач (3 примера)

4. Закрепление изученного материала

5. Домашнее задание Решение задач № 1732 – 1736 [2], стр.65-75 [4] прочитать

1 Геометрическое истолкование задачи в стандартной форме в случае двух переменных

Задача линейного программирования в стандартной форме с двумя переменными имеет вид:

	(2.13)
	(2.14)
	(2.15)

Эти задачи допускают простое геометрическое истолкование.

Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных x₁, x₂ можно изобразить точкой на плоскости, если ввести систему координат и по одной оси откладывать x₁, а по другой - x₂. Выясним, что геометрически означает совокупность решений одного отдельно взятого неравенства:

a₁x₁ + a₂x₂ ≤ b.

Рассмотрим прямую на плоскости с уравнением a₁x₁ + a₂x₂ = b.

Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой - противоположное. Для того, чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находится во всех соответствующих полуплоскостях, т.е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных x₁ ≥ 0 и x₂ ≥ 0 приводят к тому, что эта область находится в первой координатной четверти.

При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР - область допустимых решений):

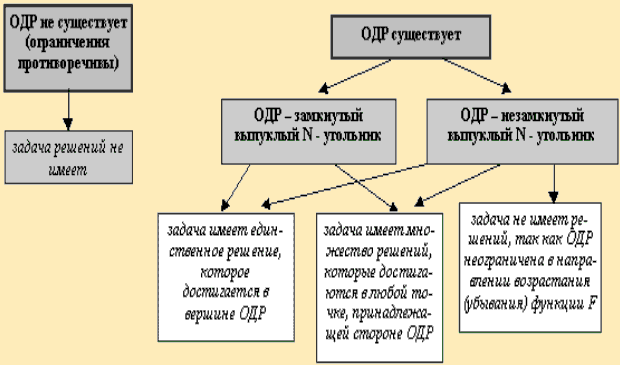
Рис. 2.3

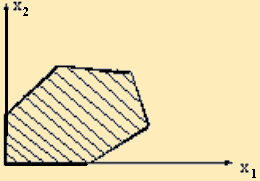
1. Основной случай - получающаяся область имеет вид ограниченного (замкнутого) выпуклого многоугольника (см. рис. 2.4).

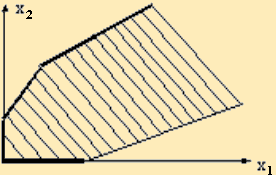
2. Неосновной случай - получается неограниченный (незамкнутый) выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 2.5.

рис. 2.4	рис. 2.5

3. Наконец, возможен случай, когда неравенства противоречат друг другу, и допустимая область вообще пуста.