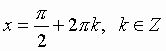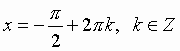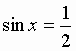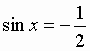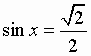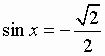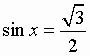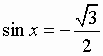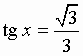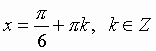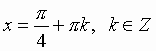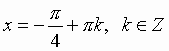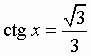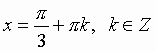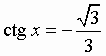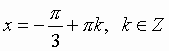Уравнения, содержащие синус - sin X.
Уравнение: |
РЕШЕНИЯ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий вид решения уравнения sin x = a, где | a | 1, определяется формулой:
x = (- 1)k · arcsin(a) + pk, k Z (целые числа),
при | a | > 1 уравнение sin x = a не имеет решений среди вещественных чисел.
Уравнения, содержащие тангенс и котангенс - tg X и сtg X
Уравнение: |
Уравнение: |
РЕШЕНИЯ: |
|
*** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*** |
|
|
Общий вид решения уравнения tg x = a определяется формулой:
x = arctg(a) + pk, k Z (целые числа).
Общий вид решения уравнения ctg x = a определяется формулой:
x = arcctg(a) + pk, k Z (целые числа).
§11. Способы решения тригонометрических уравнений
§12. История названий
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математикомТомасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Добавить список литературы!!!