Математика, 1 курс. Преподаватель Кувшинова Е.Г.

Тема: «тригонометрические функции»

§1. Градусное и радианное измерение угловых величин

Фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости, называется углом.

Если стороны угла, образуют прямую, то такой угол называется развёрнутым. Величина развёрнутого угла равна 180°.

О тметим на оси Ох справа от начала координат точку А и проведём через неё окружность с центром в точке О. Радиус ОА называется начальным радиусом.

Условились: если повернуть начальный радиус около точки О по часовой стрелке, то угол поворота считать отрицательным; если повернуть начальный радиус около точки О против часовой стрелки, то угол поворота считать положительным

За единицу измерения углов и дуг принимают соответственно угол в 1 градус и дугу в 1 градус (обозначают 1°). Угол в 1 градус – угол, который опишет начальный радиус, совершив часть полного оборота вокруг своей начальной точки против часовой стрелки. Минутой обозначают часть градуса (обозначают 1′). Секундой называется часть минуты (обозначают 1′′).

П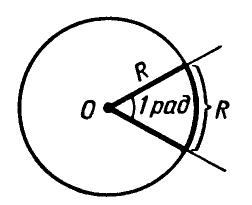 ри радианном измерении дуг за единицу измерения принимается дуга, длина которой равна радиусу этой дуги. Эта дуга называется радианом.

При радианном измерении углов за единицу измерения принимается центральный угол, опирающийся на дугу в 1 радиан.

Если начальный радиус совершит один полный оборот, то получится угол, равный 360° или 2π радианам.

Радианная мера 1° равна .

Отношение длины дуги окружности (L) к длине её радиуса (R) называется радианной мерой этой дуги:

Формула перехода от градусного измерения к радианному имеет вид:

Формула перехода от радианного измерения к градусному имеет вид:

§2. Числовая окружность

Окружность с центром в начале координат и радиусом, равным 1, называется единичной окружностью.

На числовой окружности, как и на числовой прямой, каждому действительному числу соответствует одна точка.

Если точка М числовой окружности соответствует числу t, то она соответствует и числу вида t+2πk, где k – любое целое число ( ), т.е. 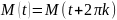. Число |k| можно рассматривать как количество полных обходов окружности в ту или иную сторону.

Расположим числовую окружность в декартовой прямоугольной системе координат xOy так, что центр совмещён с началом координат, а её радиус принимается за масштабный отрезок. Начальная точка А числовой окружности совмещена с точкой (1; 0) на оси х. При этом В=В(0; 1), С=С(-1; 0), D=D(0; -1). Каждая точка числовой окружности имеет в системе xOy свои координаты, причём для точек:

п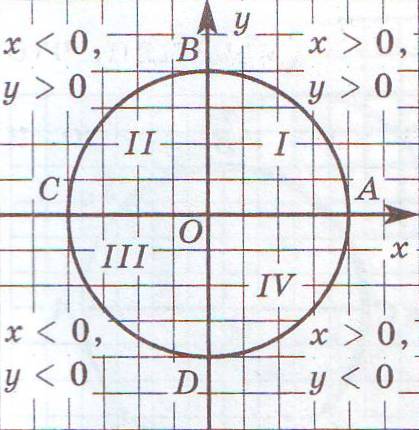 ервой четверти: ;

второй четверти: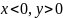

третьей четверти: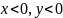

четвёртой четверти: .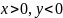

Для любой точки M(x; y) числовой окружности выполняются неравенства:

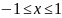и .

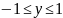Для отыскания точек на числовой окружности, удобно использовать макет числовой окружности или тригонометрический круг.

§3. Тригонометрические функции числового аргумента

Рассмотрим единичную окружность.

Е сли точка M числовой окружности соответствует числу t, то абсциссу точки M называют косинусом числа t и обозначают , а ординату точки M называют синусом числа t и обозначают .

Итак,

если M(t)=M(x; y),

то , y .

Отсюда следует, что

;

.

Отношение синуса числа t к его косинусу называется тангенсом числа t:

Область определения тангенса – множество всех действительных чисел, кроме чисел вида , .

Отношение косинуса числа t к его синусу называется котангенсом числа t:

О бласть определения котангенса – множество всех действительных чисел, кроме чисел вида , .

Знаки тригонометрических функций по четвертям:

Свойства чётности и нечётности тригонометрических функций выражается формулами:

(нечётная функция);

;

.
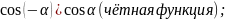
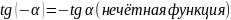