3. Экспоненциальная модель

Предположение о том, что рост интенсивности движения будет проходить по экспоненциальной модели имеет следующее математическое выражение

, (3.11)

которое для интенсивности движения в последний год срока службы (Т_сл) принимает вид

, (3.12)

где - среднесуточная интенсивность движения в году t (при t≤Т_сл), авт/сут;

- наблюдаемая среднесуточная интенсивность движения в последний год перед реконструкцией дорожной одежды (авт/сут) или прогнозируемая интенсивность движения в последнем году строительства перед пуском дороги в эксплуатацию (авт/сут): =N₁/e^P;

Р- прирост интенсивности движения (в долях единицы), который можно принимать как постоянной, так и переменной величиной за срок службы (Т_сл) дорожной одежды;

е – основание натурального логарифма;

- среднесуточная интенсивность движения в последний год срока службы дорожной одежды, авт/сут.

Коэффициент суммирования для экспоненциальной модели равен

, (3.13)

а суммарное количество приложения нагрузки за период Т_сл составит

. (3.14)

Контроль вычислений можно выполнить по формуле (3.5) при условии, что интенсивности устанавливают по зависимости (3.11).

3.4. Степенная модель

В ОДН 218.046-01 использована степенная модель прогнозирования интенсивности движения вида

, (3.15)

которая при t=1

, (3.16)

где - среднесуточная интенсивность движения в последний год срока службы дорожной одежды, авт/сут;

N₁ - среднесуточная интенсивность движения в первый год срока службы дорожной одежды, авт/сут;

q – показатель прироста интенсивности движения, определяемый по зависимости

, (3.17)

где Р – прирост интенсивности движения ( ), доли единицы.

Учитывая, что интенсивность N₁ определяется по зависимости

, (3.18)

получаем по выражению (3.16), что

, (3.19)

где N_o – наблюдаемая среднесуточная интенсивность движения в последний год перед реконструкцией дорожной одежды (авт/сут) или прогнозируемая интенсивность движения в последнем году строительства перед пуском дороги в эксплуатацию (авт/сут): =N₁/(1+P);

Среднесуточную интенсивность движения в году t (при t≤Т_сл) определяют по формуле

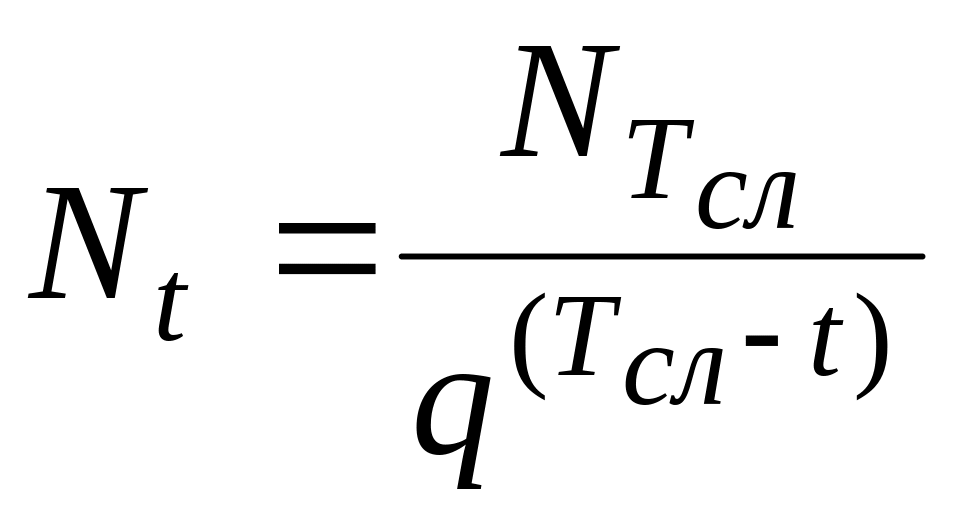(3.20)

после вычисления параметра по зависимости (3.16) или (3.19).

Коэффициент суммирования степенной функции (3.15) устанавливают по выражению

. (3.21)

Если q=1, то К_С=Т_сл

Так как в структуру формулы (3.15) не входит интенсивность No, то суммарное количество приложений нагрузки за период Т_сл устанавливают не по формуле (3.4), а по зависимости

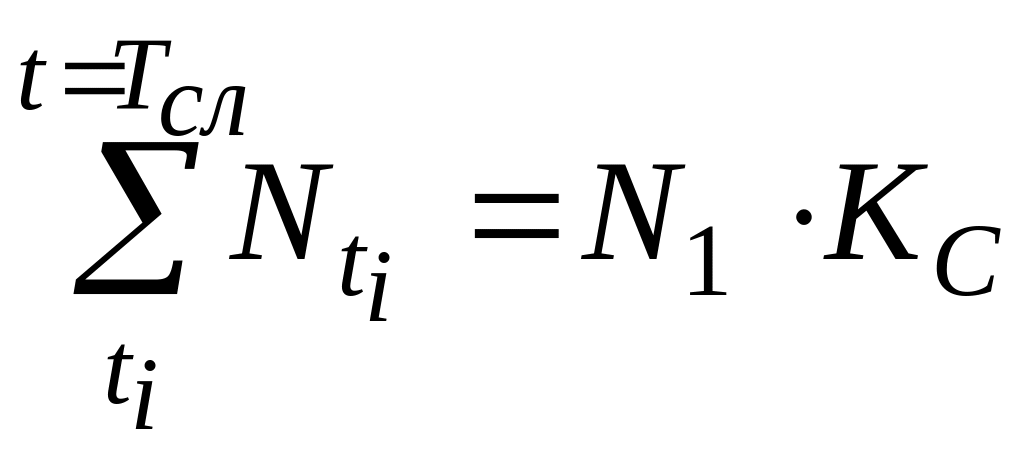. (3.22)

Контроль вычисления суммарной нагрузки выполняют по формуле (3.5) при условии, что интенсивность движения в любой промежуточный год t определяют по формуле (3.20).

Степенная модель, реализованная по формуле (3.15), работает аналогично модели роста интенсивности движения по сложным процентам [см. формулу (3.6)] в том случае, когда в формуле (3.6) используется постоянная величина прироста (Р) интенсивности, то есть при Р=const. Это объясняется тем, что формула сложных процентов то же является степенной функцией, однако имеет больше возможностей по сравнению с формулой (3.15), так как применима при P≠const.