4. Электромагнитные колебания

4.1. Основные формулы и соотношения

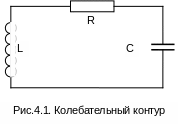
 Колебательным контуром (рис. 4.1) называется электрическая цепь содержащая индуктивность , емкость и омическое сопротивление . Сопротивление определяется в омах, индуктивность в генри. Если

= 0, то контур называется идеальным. При отсутствии емкости в цепи принимается что .

 Дифференциальное уравнение затухающих электромагнитных колебаний имеет вид:

, (4.1)

где

 здесь – заряд на конденсаторе; – собственная циклическая частота; и – соответственно индуктивность и емкость контура; – коэффициент затухания контура; – омическое сопротивление контура.

Если то уравнение (3.1) переходит в дифференциальное уравнение не затухающих электромагнитных колебаний:

. (4.2)

 При условии или уравнение (3.1) имеет решение:

, (4.3)

где

,

или

, (4.4)

– циклическая частота затухающих колебаний. Если , то .

 Разделив выражение (3.3 ) на емкость , получим:

. (4.5)

 Величина тока в контуре определяется выражением:

, (4.6)

причем .

 Затухание колебаний в контуре принято описывать логарифмическим декрементом затухания

. (4.7)

 Колебательный контур часто характеризуют его добротностью Q, которая определяется так:

, (4.8)

где – число колебаний в контуре. По прохождении колебаний амплитуда уменьшилась в раз.

 При слабом затухании

. (4.9)

 Установившиеся вынужденные колебания тока при последовательном включении в контур напряжения :

, (410)

где

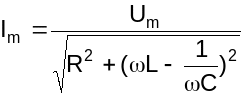. (3.10а)

 Сдвиг фаз между током и напряжением определяется выражением:

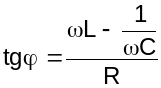. (3.11)

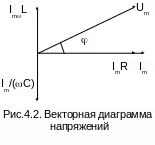
Векторная диаграмма напряжений показана на рис.4.2.

Мощность, выделяемая в цепи переменного тока:

, (4.12)

где

, (4.12a)

(4.12б)

- действующие (эффективные) значения напряже­ния и тока.

 Резонансная частота для заряда и напряжения на конденсаторе имеет вид:

. (4.12в)

При малом затухании, т.е. при резонансную частоту для напряжения можно полагать равной :

. (4.12г)

4.2. Примеры решения задач

Задача 1. Два конденсатора емкостью 0,4 мкФ и 0,5 мкФ включены последовательно в цепь переменного тока напряжением 220 В и частотой 50 Гц . Найти: 1) силу тока в цепи ; 2) падение потенциала на первом и втором конденсаторах.

Решение: Величина тока в такой цепи определяется по закону Ома:

. (4.13)

Так как и , то

, (4.14)

где – суммарная емкость обоих конденсаторов; она определяется выражением

или . (4.15)

Величина циклической частоты определяется выражением:

(4.16)

и тогда

. (4.17)

Подставив числовые данные в системе СИ, получим:

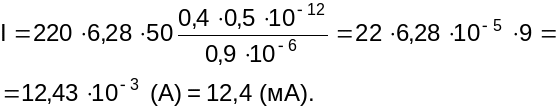
Так как цепь последовательная, то

(4.18)

Но (Это следует из (3.14)). Подставив , и _, получим:

,

Ответ : = 12,4 мА; = 98,7 B; = 121,3 B.

Задача 2. Колебательный контур содержит емкость 0,1 мкФ, индуктивность 0,2 мГн и активное сопротивление 10 0м. Вычислить: а) логарифмический декремент затухания ; б) добротность контура .

Решение: Величина логарифмического декремента затухания описывается выражением

(4.19)

Подставив числовые данные в системе СИ, получим:

Величина определяется соотношением:

. (4.20)

Подставив числовые данные в (3.20), получим:

.

Ответ : 0,70 ; 4,45.

Задача 3. Колебательный контур содержит конденсатор емкостью 0,4 мкФ, активное сопротивление 100 Ом и индуктивность катушки 100 мГн. Найти: а) частоту затухающих колебаний , б) его добротность.

Решение: Частота затухающих колебаний определяется выражением:

, (4.21)

где и – параметры контура.

Подставив числовые данные, получим:

Величина добротности вычисляется так:

. (4.22)

Подставив в (3.22) числовые данные, получим:

Ответ : 15 кГц, 1,58.