6.2. Примеры решения задач

Задача 1. Напряжение меняется с периодом мс (0,02 с) и при , где В/с. Найти амплитуды и фазы первых трех гармоник , , , .

Решение: Поскольку функция нечетная, то в силу формулы (5.4) все коэффициенты , а начальная фаза в уравнении (5.3) для всех . Тогда на основании формул (5.6) и (5.5)

. (6.27)

После подстановки данных получим: = 0,318 В; 0,159 В; 0,106 В.

Задача 2. Построить фазовую траекторию сигнала , ограниченного сверху и снизу на уровне 0,5 В; если 1 В; 0,1 с.

Решение: 1. Взяв производную от , найдем :

.

2. Исключим из уравнений для напряжения и его производной время, для чего выразим из них синус и косинус аргумента, возведем их в квадрат и сложим:

(6.28)

При значениях , для которых , уравнение (5.28) является уравнением в общем виде части фазовой траектории. При остальных значениях наступает ограничение: и . Фазовая траектория после подстановки данных будет описываться уравнением

п ри В, а при В переходит в вертикальные отрезки, как показано на рис.6.3.

Задача 3. Найти отношение амплитуды третьей гармоники к амплитуде первой гармоники для синусоидального сигнала, ограниченного на уровне :

(6.29)

Определить коэффициент нелинейных искажений этого сигнала.

Решение: 1. Поскольку преобразованный сигнал задан кусочно, найдем значение моментов времени в точках излома:

, ,

где меньший индекс относится к отрицательному моменту времени.

Таким образом функция в интервалах времени , и описывается верхней ветвью формулы (6.29), а в интервалах времени и ее нижней ветвью. Здесь .

2. Найдем коэффициенты преобразования Фурье:

-

; (6.30)

- . (6.31)

3. После интегрирования, обозначив , получим, что

и

. (6.32)

4. Найдем коэффициент нелинейных искажений, используя формулу (5.18), результаты интегрирования (6.31) и формулу (6.32).

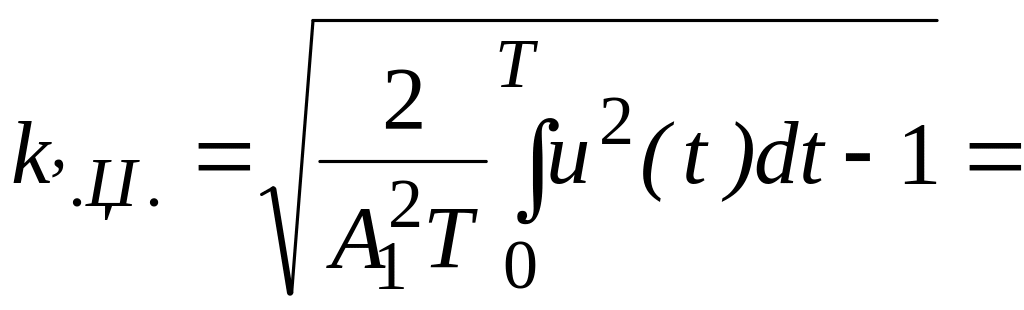
. (6.33)

В целях проверки найдем коэффициент нелинейных искажений для . В этом случае , и после подстановки их в формулу (6.33) получим .

Задача 4. Нелинейный осциллятор совершает колебания согласно дифференциальному уравнению при 100 В²/с². Определить методом гармонического баланса приближенный период колебаний при значениях амплитуды колебаний от 1 В до 10 В через 1 В.

Решение: 1. Поскольку восстанавливающая функция в ряд Маклорена не разлагается, метод малых колебаний не применим. Нечетность восстанавливающей функции и необходимость определения зависимости периода колебаний от их амплитуды делают возможность применения метода гармонического баланса.

На основании формулы (5.26) определим квадрат циклической частоты основной гармоники колебаний:

^,

где – амплитуда колебаний. Отсюда период колебаний

. (6.34)

2. Вычислим период колебаний и составим таблицу его зависимости от амплитуды .

Таблица 6.1

A, В	1	2	3	4	5	6	7	8	9	10
T, с	0,444	0,889	1,332	1,777	2,221	2,666	3,110	3,554	3,999	4,443