Порядок выполнения задания 2

1. На листе формата 12(A3) начертить рамку, отступив от левого края листа 20 мм и по 5 мм от других краев.

2. В нижнем правом углу начертить и заполнить штамп размером 185х55 мм.

3. В верхнем правом углу начертить прямоугольник для размещения таблиц размером 150х80мм.

4. В верхнем правом углу чертежа указать координаты вершин пирамиды в соответствии с заданием.

5. Нанести оси координат. Для определения местонахождения на чертеже начала координат (т. 0) следует проанализировать задание: определить вершину с наибольшей координатой Х (первая - координата в скобках: в рассматриваемом примере 115 мм). Прибавить к этой координате 15 мм и полученный размер отложить от левой линии рамки. На этом расстоянии провести вертикальную линию. Затем выбрать вершину с наибольшей' координатой Z (последняя цифра в скобках: в рассматриваемом примере 100 мм), прибавить к этой координате 15 мм и полученное расстояние отложить от верхней линии рамки. Через полученную точку провести горизонтальную линию. На пересечении линий поставить точку О - начало координат.

6. Обозначить оси, при чем ось, отходящую от точки О влево, обозначить OX₁₂, т.к. эта ось пересечения горизонтальной П₁, и фронтальной П₂ плоскостей проекций; ось, отходящую вверх, обозначить OZ₂₃- т.к. она является пересечением фронтальной П₂ и профильной П₃ плоскостями проекций. Ось, отходящую вниз от точки О, обозначить OY₁, поскольку она образована пересечением горизонтальной П₁, и профильной П₃ плоскостями проекций, но при "разрыве" осталась на плоскости П₁. Ось, отходящую влево от начала координат, обозначить Y₃, т.к. она после "разрыва" осталась на плоскости П_з.

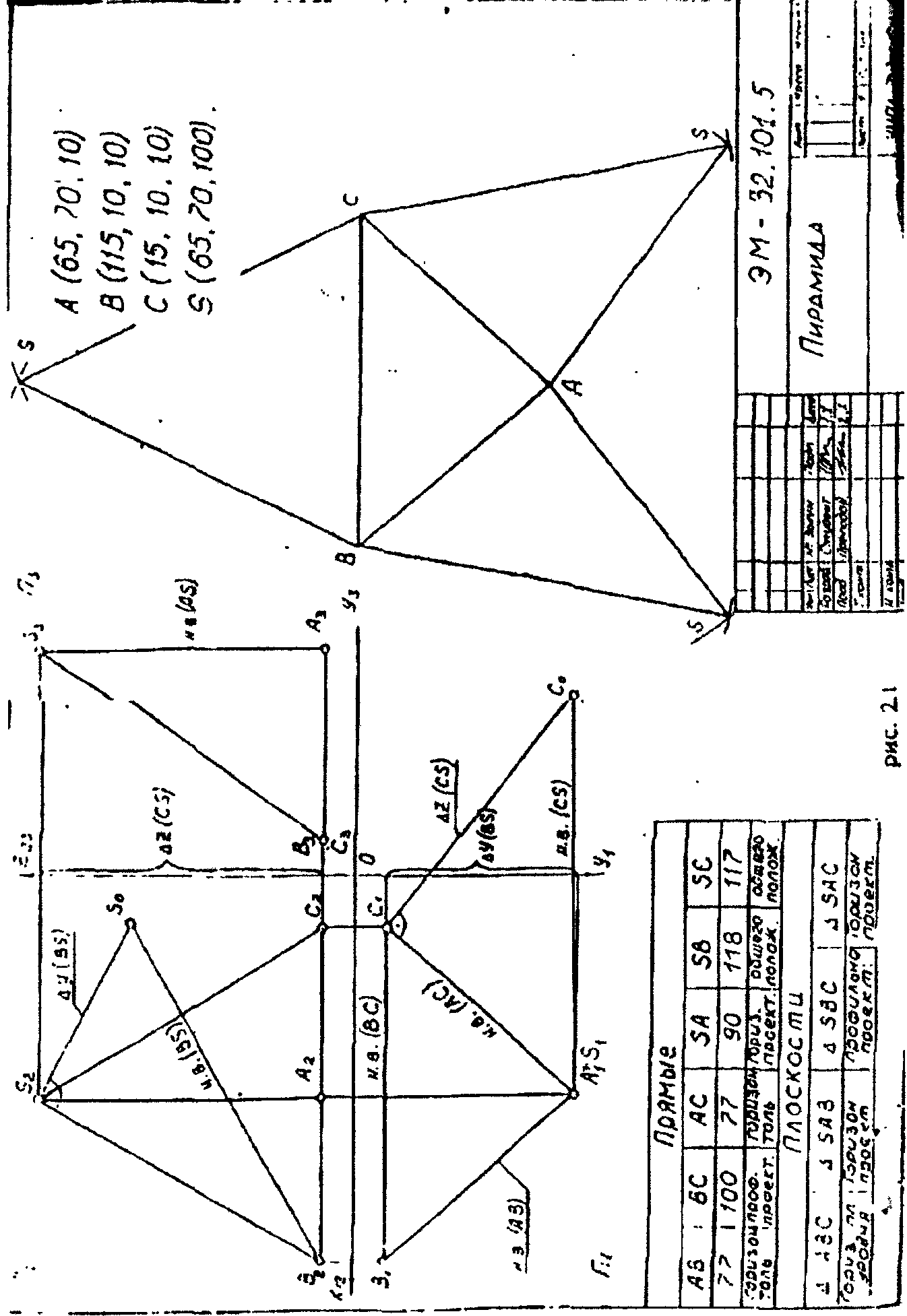
7. Построить проекции вершин А, В, С, S пирамиды. Для построения горизонтальной проекции точки, т.е. проекции точки на плоскость П₁ представляющей на чертеже координатную систему X₁₂OY₁, следует отложить вдоль осей отрезки, соответствующие координатам Х и Y точки. Проекция точки будет найдена как точка пересечения прямой, проходящей через точку с координатой (Х,0) параллельно оси OY₁, и прямой, проходящей через точку с координатой (0,Y) параллельно оси Х₁₂.

В рассматриваемом примере для построения горизонтальной проекции точки А(65,70,10) необходимо провести от осей через концы соответствующих, отрезков (рисунок2.2) перпендикулярные прямые, точка пересечения которых будет проекцией точки А на горизонтальную плоскость проекции П₁ -точкой A₁.

Для построения фронтальной проекции точки А следует провести линию связи, проходящую через горизонтальную проекцию - точку A₁, перпендикулярно оси 0X₁₂. Затем на этой линии отложить отрезок, длина которого равна координате Z точки А(в рассматриваемом примере Z= 10). Полученная точка А₂ -фронтальная проекция точки А (см. рисунок 2.2). Для построения профильной проекции точки А следует провести линию проекционной связи через проекцию точки А на плоскость П₃, - точку А₂ перпендикулярно оси 0Z₂₃. Точка пересечения этой прямой и прямой, перпендикулярной оси 0Y₃, проходящей через точку на этой оси от стоящей от центра координат на расстоянии Y (в рассматриваемом примере Y=70), будет точкой A₃ - профильной проекции точки А. Есть другие способы построения профильной проекции точки А. Аналогично следует построить проекции трех других вершин пирамиды.

8. Построить проекции ребер пирамиды следует, соединив проекции вершин на одну плоскость прямыми, т.е. А₁ с В₁, А₂ с В₂, А_З с В_З и т.д. Ребра, которые на данной проекции не видны, необходимо показать пунктирной линией.

9. Для того, чтобы определить натуральную величину ребер пирамиды и заполнить первую часть таблицы, необходимо проанализировать расположение ребер по отношению к плоскостям проекций на предмет выявления особых прямых, проекции отрезков которых проецируются на соответствующие плоскости проекций в натуральную величину. Название особых прямых и их признаки приведены в таблице 2.3.

Р исунок 2.2

ПРИМЕЧАНИЕ к таблице 2.3:

П₁ - горизонтальная плоскость проекции;

П₂- фронтальная плоскость проекции;

П₃- профильная плоскость проекции;

|| - знак параллельности;

- знак перпендикулярности.

В рассматриваемом примере отрезок АВ в натуральную величину проектируется на плоскость П₁, т.е. длина отрезка A₁B₁ -натуральная величина отрезка АВ. т.к. прямая АВ - линия уровня, а именно - горизонтальная прямая, не имеющая свойств, указанных в таблице 2.3, называемая прямой общего положения. Найти натуральную величину отрезка общего положения можно несколькими методами.

Рассмотрим метод прямоугольного треугольника. На одной из плоскостей проекции необходимо построить прямоугольный треугольник, один катет которого - проекция отрезка на эту плоскость, а другой - разность расстояний от конца данного отрезка до этой же плоскости проекции или, что то же самое, разность координат концов отрезка на другой проекции.

В рассматриваемом примере для определения истинной величины отрезка SC на проекции П₁ из точки C₁, восстановлен перпендикуляр, на котором отражен отрезок, длина которого равна разности координат Z = Z_S2 - Z_C2, после чего точка С₀ соединена отрезком с точкой S₁. Длина отрезка C₀S₁ - истинная величина отрезка SC.

Необходимо измерить натуральные величины отрезков и занести их в таблицу.

10. Определить, какие из граней пирамиды лежат в особых плоскостях. Признаки и названия особых плоскостей приведены в таблице 2.4. В рассматриваемом примере плоскость, в которой лежит грань SAB - горизонтально-проектирующая, т.к. ее проекция на П₁, - прямая линия A₁B₁(точки A_l и S_l - совпали).

11. Рассмотрим построение развертки пирамиды методом треугольника. С помощью циркуля из произвольно выбранной точки (в рассматриваемом примере точка А) отложить отрезок, равный натуральной величине отрезка АВ, затем начертить дуги радиусами АС и ВС. Их пересечение -точка С. Начертить отрезки АС и ВС. Аналогично построить другие ребра.

12. Перед составлением программы ознакомиться с необходимыми теоретическими положениями [12] и методикой составления программ на языке MATLAB, рассмотренной в приложении 1. Пример составления программы приводится ниже.

clc; clear; more off; echo on; clf;

% Задание 2. Создание изображения пирамиды и ее

% ортогональных проекций.

% Курс "Инженерная и машинная графика"

% Выполнил ст. гр. ДРЭ-Сх-х Иванов И.И.

% (с) 2001 р. УИПА, кафедра СУ и АПУ

% Версия 8.7.2001 г.

% file exerc2.m

date

echo off;

% Формируем массивы координат опорных точек вершин пирамиды

х=[65, 65, 65,65;

115,65,115,65;

15,115, 15, 15];

у=[70,70,70,70;

10,70,10,70;

10,10,10,10];

z=[10,100,100,100;

10, 10, 10, 10;

10, 10, 10, 10];

% Задаем окраску граней пирамиды

c(1:3,1)=ones(3,1);

c(1:3,2)=ones(3,1)*2;

c(1:3,3)=ones(3,1)*3;

c(1:3,4)=ones(3,1)*4;

% Прорисовываем грани

fill3(x,y,z,c);

% Маркируем оси и даем название рисунку

set(gca, 'FontName', 'Times New Roman Cyr');

set(gca, 'FontSize', 12);

хlаbеl('Ось X'); уlаbеl('Ось У); zlabel('Ocь Z');

title('Аксонометрическая проекция');

% Включаем режим "сетки"

grid on

% Маркируем вершины пирамиды

text(65,70,10,'A'); text(115,10,10,'В'); text(15,10,10,'С');

text(65,70,100,'S'); view([150,150,150]);

pause

% Переходим к просмотру проекций в ортогональной проекции

title('Фронтальная проекция'');

view([0,-150,0]);

pause

title('Профильная проекция');

view([150,0,0]);

pause

title(‘Горизонтальная проекция');

view([0,0,150]);

Обратите внимание, что при формировании массивов опорных точек пирамиды необходимо в каждом столбце матриц X, Y и Z соблюдать строгое соответствие координат выбранному порядку плоскостей, например в указанном примере для матрицы по координате Х порядок следующий:

Пл. АВС SAB SBC SAC

Также учитывайте, что коэффициент выбора цветовой гаммы для оператора fill3, ограничен диапазоном 17.

ЗАДАНИЕ 3. Выполнить чертеж, на котором:

• создать «скелетную» модель трехмерного объекта, на основе чертежа платы (задание 5);

• создать в прямоугольной ортогональной системе проецирования три проекции трехмерного объекта;

• создать в прямоугольной ортогональной системе проецирования аксонометрическую проекцию трехмерного объекта;

Составить программу на языке MATLAB выполняющую следующие действия:

• формирование массивов опорных точек ребер трехмерного объекта;

• построение изображения аксонометрической проекции трехмерного объекта;

• построение изображение ортогональных проекций трехмерного объекта;