2.4. Методические рекомендации по выполнению лабораторных работ.

Перед проведением лабораторной работы необходимо получить инструктаж по технике безопасности и расписаться в журнале ТБ и журнале проведения лабораторных работ.

Необходимо ознакомиться с описанием лабораторной работы, выписать расчетные зависимости, приведенные в теоретической части описания лабораторной работы. Выполнить лабораторную работу, с записью измеряемых величин на специальные бланки. При возникновении нештатной ситуации (обрыва питающего электрокабеля, разрыва резиновой трубки и т. п., прекратить выполнение работы и ничего не трогая, обратиться к преподавателю). Используя расчетные зависимости, провести обработку результатов измерений, внеся результаты вычислений в специальные бланки. Оформить контрольную работу в виде единого документа (тетрадь и т. п.).

При сдаче лабораторной работы следует знать теоретическую часть лабораторной работы, порядок выполнения работы, иметь представления о физических причинах расхождения теоретических и опытных значениях рассчитываемых величин, источниках систематических и случайных погрешностях.

Лабораторная работа № 1. Относительный покой жидкости. Определение формы свободной поверхности жидкости во вращающемся цилиндрическом сосуде.

Жидкость в цилиндрическом сосуде, вращающемся с постоянной угловой скоростью находится в состоянии покоя относительно сосуда.

Теоретической основой этого явления служит уравнение равновесия Эйлера, в котором, в данном случае, входят сила тяжести и центробежная сила.

Исследования показывают, что в этом случае свободная поверхность жидкости получает вид параболоида вращения с вертикальной осью, совпадающей с осью сосуда. Отметки точек параболической свободной поверхности относительно горизонтальной плоскости, проходящей через наинизшую точку свободной поверхности параболоида находятся по теоретической зависимости вида:

где - угловая скорость вращения цилиндра

- кратчайшее расстояние от данной точки свободной поверхности до оси вращения, см,

,

n – частота вращения.

Схема установки

Установка состоит из литого корпуса, на котором вращается цилиндрический сосуд, в котором залито трансформаторное масло. Система электропривода позволяет менять частоту вращения сосуда.

Над цилиндром установлена рама, по которой движется каретка с измерительной иглой. При ручном вращении ручки каретка и игла перемещаются в горизонтальном направлении. Вертикальные перемещения иглы производятся с помощью специальной рукоятки. При этом на поверхности штока иглы нанесена шкала, по которой регистрируются вертикальные координаты свободной поверхности по нониусу.

Регулирование частоты вращения цилиндра от до позволяет получить семейство параболических кривых свободной поверхности.

Задачи работы

1. Поставить измерительную иглу на отметку «0» по горизонтальной шкале, при этом ось иглы совпадает с осью сосуда.

2. Опустить вращением рукоятки измерительную иглу до соприкосновения с поверхностью жидкости и взять отсчет по нониусу.

3. Поднять иглу вверх и перемещать в горизонтальном направлении на 1 – 2 см и каждый раз опускать ее до соприкосновения с поверхностью масла.

Всего взять 7 – 8 точек по радиусу.

4. Найти отметки точек свободной поверхности как разность отметок точек свободной поверхности и отметки наинизшей точки параболоида (отметки по вертикали точки в центре сосуда при ).

5. Вычислить теоретические значения отметок свободной поверхности по формуле .

6. Сопоставить отметки с величиной и подсчитать расхождение в процентах между этими величинами:

7. Произвести построение теоретической и экспериментальной кривых свободной поверхности.

Лабораторная работа № 2. Демонстрация уравнения Бернулли. Построение пьезометрической и напорной линий при движении жидкости в трубопроводе

Уравнение Бернулли для потока реальной жидкости при установившемся движении (рис. 1) имеет вид:

Рис.1

Уравнение Бернулли можно рассматривать с двух точек зрения: геометрической и энергетической.

С геометрической точке зрения:

(геометрическая высота) – расстояние от произвольно выбранной горизонтальной плоскости сравнения 0 – 0 до центра тяжести рассматриваемого сечения.

Линия, соединяющая центры тяжести сечений, называется осью потока.

- геометрический уклон, который может быть как положительным, так и отрицательным;

- пьезометрическая высота, измеряемая пьезометром;

- гидростатический напор.

Линия, соединяющая уровни жидкости в пьезометрах, называется пьезометрической линией.

- пьезометрический уклон, который может быть как положительным, так и отрицательным;

- скоростной напор;

- коэффициент кинетической энергии, учитывающий неравномерность распределения скоростей в поперечном сечении потока;

- полный гидродинамический напор.

Линия, соединяющая значение полного напора в каждом сечении, называется напорной линией или линией полной удельной энергии.

- гидравлический уклон, который может быть только положительным;

- потеря напора между рассматриваемыми сечениями;

- удельная потенциальная энергия положения;

- удельная потенциальная энергия давления;

- суммарная удельная потенциальная энергия;

- удельная кинетическая энергия;

- полная удельная энергия.

Из бака 1 (рис. 2) вода поступает в горизонтальный трубопровод переменного сечения 2 диаметрами и . На этом трубопроводе шесть сечений, расстояния между которыми Для измерения пьезометрических высот в этих сечениях установлены пьезометры 3, показания которых определяются по миллиметровой шкале. Расход воды определяется по ротаметру 4.

Ротаметр представляет собой вертикально установленную коническую стеклянную градуированную трубку, где помещен поплавок, удельный вес которого больше удельного веса протекающей жидкости. При движении жидкости по трубке снизу вверх поплавок поднимается вверх до тех пор, пока не займет такое положение, когда перепад давления, обусловленный сопротивлением кольцевого сечения, образованного поплавком и трубкой (перепад давления вызывает гидродинамическую силу), уравновесит разницу в весе самого поплавка и жидкости в объеме поплавка. Схема установки

Рис. 2

Таким образом, определенному расходу жидкости соответствует определенная высота подъема поплавка. Чтобы определить расход, надо вначале зафиксировать по ротаметру высоту поднятия поплавка h, а затем, найти расход Q по тарировочной кривой, которая строится при предварительных тарировочных испытаниях.

Клапаны 6 служат для выпуска воздуха при заполнении системы водой.

Задачи работы

В условиях установившегося неравномерного движения жидкости в трубе переменного сечения (рис. 2) следует:

1. определить значение удельной потенциальной энергии в заданных сечениях потока, проведя плоскость сравнения через ось трубы;

2. вычислить для тех же сечений значения удельной кинетической энергии , а также полной удельной энергии и потерь напора ;

3. по полученным результатам построить линии: пьезометрическую и напорную (линию полной удельной энергии).

Лабораторная работа № 3. Определение коэффициента гидравлического трения в трубопроводе круглого сечения

В этой работе рассматриваются только потери по длине (рис. 3), которые принято определять по формуле Дарси – Вейсбаха:

,

где - коэффициент гидравлического трения;

- длина трубопровода;

- диаметр трубопровода.

Р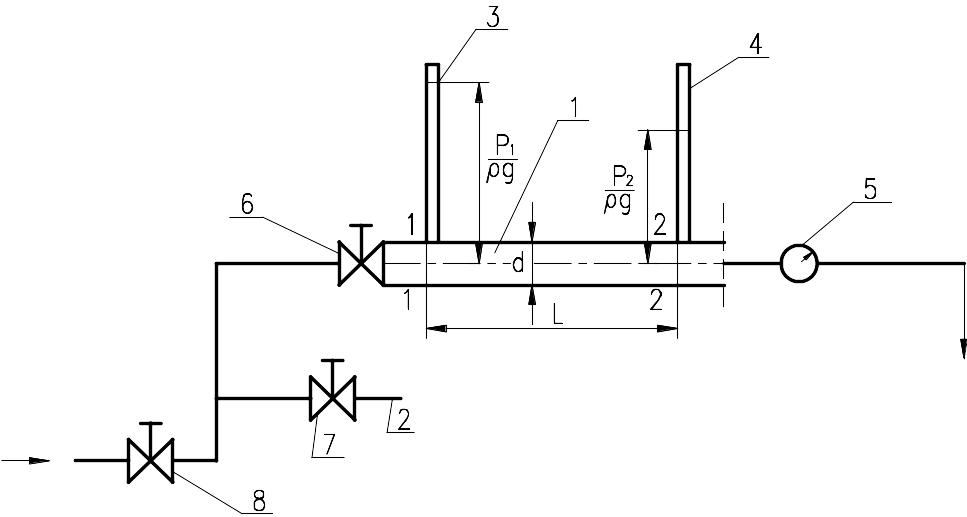 ис. 3

Из формулы коэффициент гидравлического трения равен:

Для определения надо знать среднюю скорость и потерю напора по длине . Средняя скорость может быть определена после измерения расхода Q крыльчатым водомером 5. Потеря напора по длине определяется разностью показаний пьезометров, установленных в начале и в конце опытного участка трубопровода длиной . Применяя уравнение Бернулли для сечений 1 – 1 и 2 – 2 получим:

Плоскость сравнения проводим по оси трубы, тогда

,

так как .

Потеря по длине из уравнения Бернулли будет равна:

В итоге определены все величины для нахождения по формуле .

Схема установки

Имеется горизонтальный трубопровод 1 постоянного диаметра . На этом трубопроводе в сечениях 1 – 1 и 2 – 2 установлены пьезометры 3 и 4, расстояние между которыми . Расход определяется по крыльчатому водомеру 5.

Задачи работы

В условиях установившегося движения жидкости в круглом напорном трубопроводе необходимо:

1. определить значение коэффициента гидравлического трения для трех значений расходов;

2. по результатам опытов построить график .

Лабораторная работа № 4. Определение коэффициента сжатия , скорости , сопротивления и расхода при истечении через малое отверстие в тонкой стенке (напор Н постоянный, сжатие совершенное)

На рисунке 4 показана схема истечения из малого круглого отверстия в тонкой стенке. Размер диаметра отверстия меньше 0,1Н, такие отверстия называются малыми.

При истечении жидкости из отверстия в тонкой стенке на расстояние 0,5d от плоскости входного отверстия происходит сжатие струи (сечение С – С). Отношение площади сжатого сечения к площади входного отверстия называется коэффициентом сжатия:

Скорость в сжатом сечении струи определяется по формуле:

,

где - коэффициент скорости;

Н – напор над центром отверстия.

Расход при истечении равен:

или ,

где - площадь входного отверстия;

- коэффициент расхода, равный произведению коэффициента сжатия и коэффициента скорости:

.

Отсюда коэффициент сжатия определяется как:

Из формулы коэффициент расхода равен:

Коэффициент скорости определяется по формуле:

Таким образом, если замерить абсциссу х и ординату у какой-либо точки струи, то можно определить коэффициент скорости .

Коэффициент сопротивления отверстия определяется по формуле:

Для малых круглых отверстий в тонкой стенке при (число Рейнольдса ), , , , .

Схема установки

Имеется цилиндрический бак 1 (рис. 4), в котором сделано круглое отверстие 2 диаметром . Напор в баке постоянный и измеряется при помощи пьезометра 3.

Р асход измеряется крыльчатым водомером 4. Координаты х, у измеряются по линейки.

Рис. 4

Краник 5 служит для выпуска воздуха. Вентиль 6 предназначен для регулировки расхода.

Задачи работы

В условиях установившегося истечения через малое круглое отверстие необходимо:

1. Вычислить значение коэффициента расхода по формуле ;

2. Замерить в любой точке струи координаты х и у, определить коэффициент скорости по зависимости ;

3. Зная и , определить коэффициенты сжатия и сопротивления и по формулам и ;

4. Сопоставить результаты со справочными данными.

Лабораторная работа № 5. Определение времени опорожнения сосуда с жидкостью при переменном напоре.

Задача истечения жидкости при переменном напоре обычно сводится к определению времени опорожнения или заполнения всего сосуда или некоторой его части в зависимости от начального наполнения, формы и размеров сосуда и отверстия. Такие задачи решают при наполнении и опорожнении резервуаров, цистерн, водохранилищ, шлюзовых камер и т.п.

Необходимо иметь в виду, что в этих случаях вследствие непрерывного изменения напора, а, следовательно, и непрерывного изменения скоростей и давлений, всегда наблюдается неустановившееся движение жидкости, поэтому при подсчетах нельзя использовать обычное уравнение Бернулли.

Теория дает следующую формулу для расчета времени опорожнения прямоугольного бака от уровня до уровня через круглое отверстие (рис. 5):

,

где - площадь сечения бака;

- коэффициент расхода (определяется экспериментально);

- площадь сечения отверстия.

Схема установки

Установка состоит (рис. 5) из бака 1 со сторонами, равными в. Истечение происходит через патрубок 3 диаметром d. Уровень жидкости регистрируется с помощью мерной трубки 2, установленной на лицевой панели бака.

Рис. 5

Задачи работы

Определение времени опорожнения прямоугольного бака с жидкостью от уровня до уровня и сравнение его с расчетами.

Лабораторная работа № 6. Измерение потери напора при внезапном расширении трубопровода.

Как известно, кроме потерь энергии по длине потока, существуют местные потери, вызванные изменением величины или направления скорости. Местные потери принято определять по формуле:

,

где - коэффициент местного сопротивления;

- средняя скорость.

Только для определения местной потери, вызванной внезапным расширением потока (рис. 6), имеется теоретическая формула, которая была получена французским ученым Борда:

,

г де - средняя скорость в трубопроводе до расширения (в сечении 1 – 1);

- средняя скорость в трубопроводе после расширения (в сечении 2 – 2).

Рис. 6

С другой стороны, величину потерь напора при внезапном расширении можно получить опытным путем из уравнения Бернулли для сечений 1 – 1 и 2 – 2 (плоскость сравнения совпадает с осью трубы):

, следовательно:

,

откуда

.

Схема установки

Имеется горизонтальный трубопровод, состоящий из трех отрезков труб 1, 2, 3 диаметрами соответственно ; ; , в которые жидкость поступает из бака 6 в бак 7, далее на слив через ротационный водомер 10.

Задачи работы

1. Определить опытным путем величину потерь напора по формуле .

2. Сопоставить между собой вычисленные величины.