5. Рівнодіюча система сил.Приклади.

Якщо на дане тіло діє одночасно декілька сил, то їх дію на рух тіла можна замінити дією однієї сіли. Таку заміну називають складанням сил. Дані сили називають складовими, а замінюючу їх силу - рівнодіючою(або їх сумою).

Рівнодіюча сил - це сила, яка замінює дію кількох сил. Рівнодіюча сила дорівнює геометричній сумі всіх сил системи . Рівнодіюча сила - теж сила і підкоряється всім їхніми правилами..

Система сил має рівнодіючу тільки в тому випадку, якщо для неї існує точка, відносно якої ,головний момент сил системи, дорівнює нулю.

1) Правило трикутника. Для складання двох векторів U та V (поставити зверху вектори) за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника , причому його початок збігається з початком першого вектора, а кінець з кінцем другого вектора. (мал.1) 2) Правило паралелограма. Для складання двох векторів U та V (поставити зверху вектори) за правилом паралелограма обидва ці вектора переносяться паралельно самим собі так, щоб їх початку збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка з їх загального початку. (мал.1)

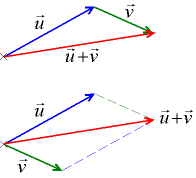(мал.1)

Рівнодіюча системи сил, наприклад двох сил, рівних за величиною і протилежних за напрямком, дорівнює нулю. Якщо вектори знаходяться на одній прямій і спрямовані в один бік, то їх сили додаються, якщо ж в різні боки – віднімаються.Для рішення використовуються геометричні формули та побудови. Як правило, вирішується прямокутний трикутник з використанням знаменитого співвідношення:

6. Поняття про матеріальну точку,абсолютно тверде тіло.Приклади

Матеріальна точка - найпростіша фізична модель в механіці - тіло, розміри якого припустимо вважати нескінченно малими по відношенню до решти об'єктів. Практично під матеріальною точкою розуміють тіло, розмірами і формою якого можна знехтувати при вирішенні даного завдання При прямолінійному русі тіла достатньо однієї координатної осі для визначення його положення. Наприклад1, Земля — велике небесне тіло, але у вивченні механічної взаємодії із Сонцем, вона може бути прийнятою за матеріальну точку, адже її радіус ~ 6400 км, а відстань до Сонця ~ 150 мільйонів км, що набагато перевищує радіус Землі.

Наприклад2, при розрахунку шляху, пройденого поїздом, можна знехтувати його розмірами, навіть якщо шлях вимірюється сантиметрами. Маса і положення матеріальної точки в кожен конкретний момент часу повністю визначають її поведінку і фізичні властивості Знехтувати розмірами об'єкта можна тільки тоді, коли він описується моделлю механічної системи, яка має тільки поступальні, але не внутрішні ступені свободи. Обмеженість застосування поняття про матеріальну точці видно з такого прикладу: в розрідженому газі при високій температурі розмір кожної молекули дуже малий у порівнянні з типовим відстанню між молекулами. Здавалося б, їм можна знехтувати і вважати молекулу матеріальною точкою. Однак це не завжди так: коливання і обертання молекули - важливий резервуар «внутрішньої енергії» молекули, «ємність» якого визначається розмірами молекули, її структурою і хімічними властивостями.

Абсолютно тверде тіло - другий опорний об'єкт механіки поряд з матеріальною точкою. Механіка абсолютно твердого тіла повністю зводиться до механіки матеріальних точок, але має власне утримання (корисні поняття і співвідношення, які можуть бути сформульовані в рамках моделі абсолютно твердого тіла), що представляє великий теоретичний і практичний інтерес. Існує кілька визначень:    1. Абсолютно тверде тіло - модельне поняття класичної механіки, що означає сукупність матеріальних точок, відстані між якими зберігаються в процесі будь-яких рухів, що здійснюються цим тілом. Інакше кажучи, абсолютно тверде тіло не тільки не змінює свою форму, але і зберігає незмінним розподіл маси всередині.    2. Абсолютно тверде тіло - механічна система, що володіє тільки поступальними і обертальними ступенями свободи. «Твердість» означає, що тіло не може бути деформоване, тобто тілу не можна передати ніякої іншої енергії, крім кінетичної енергії

   3. Абсолютно тверде тіло - тіло (система), взаємне положення будь-яких точок якого не змінюється, в яких би процесах воно не брало участь.

Абсолютно твердих тіл в природі не існує, проте в дуже багатьох випадках, коли деформація тіла мала і їй можна знехтувати, реальне тіло може (наближено) розглядатися як абсолютно тверде тіло без шкоди для завдання.