37. Предмет кінематики. Основні поняття. Приклади.
Кінематикою називають розділ теоретичної механіки, в якому вивчаються загальні властивості і якості різних механічних рухів з геометричної точки зору без урахування причин, що викликають і змінюють ці рухи.
Кінематику можна розглядати як перехідну ступінь від геометрії до механіки – вона є геометрією чотирьох вимірів, бо крім трьох вимірів, прийнятих в геометрії, запроваджується четвертий – час. Кінематика для свого викладання не потребує ніяких нових аксіом, і спирається на аксіоми евклідової геометрії.
В задачах кінематики час приймається за незалежну змінну (аргумент). Відлік часу ведеться від певного початкового моменту, котрий обирають відповідно до конкретних умов задачі.
Кінематично задати рух матеріального об’єкту (тіла, точки) – означає задати положення цього об’єкту відносно обраної системи відліку в будь-який момент часу. Якщо положення об’єкта визначається певними параметрами, то необхідно задати залежність параметрів від часу. Така залежність називається кінематичними рівняннями руху або законом руху.
Основними питаннями кінематики є виявлення математичних способів задання руху і методів визначення всіх кінематичних величин, що характеризують даний рух.
38Природний спосіб подання точки в кінематиці.
Природний спосіб задання руху використовують у випадках, коли траєкторія наперед відома. Тоді положення точки в просторі визначається (рис.2.2)
просторовою кривою
(траєкторією точки);криволінійною (дуговою) координатою
на траекторії;початком відліку дугової координати;
напрямом додатного відліку дугової координати.
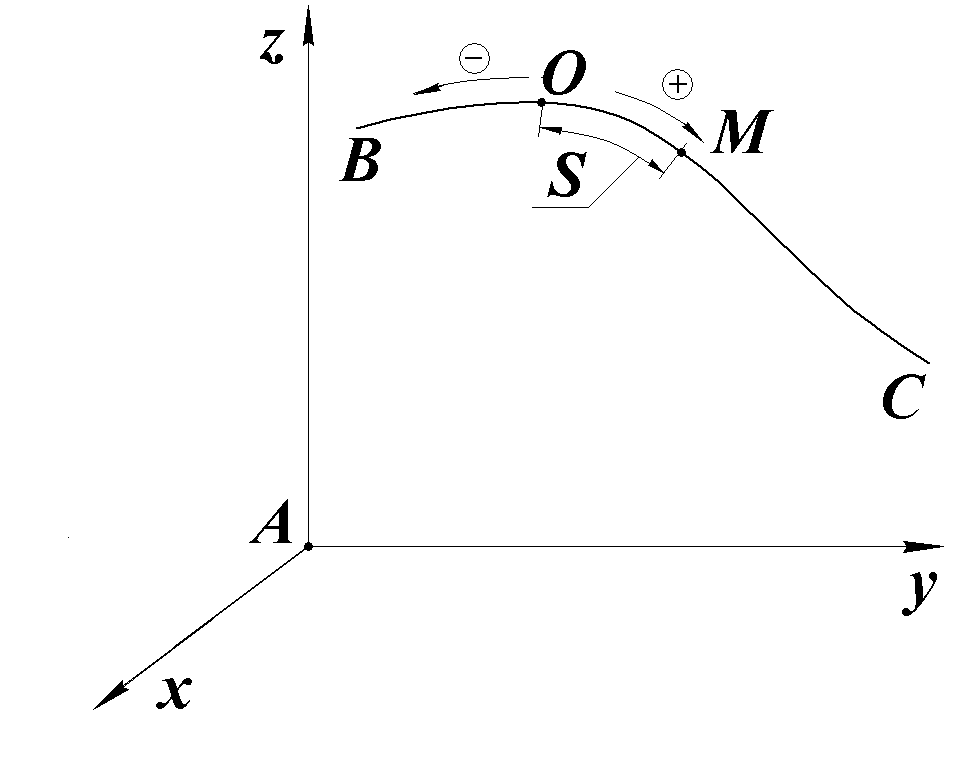
Рис. 2.2
При русі точки по
траєкторії дугова координата змінюється
з часом, тобто
.(2.4)
Залежність (2.4) називають законом руху точки вздовж заданої траєкторії.
Дугову координату не можна плутати з довжиною шляху, який пройшла точка.
Шлях точки – це відстань, що пройдена нею за певний проміжок часу, яка вимірюється вздовж траєкторії в напрямку руху точки.
Дугова координата – положення точки на траєкторії в даний момент часу.
39Визначення швидкості та прискорення при природному поданні руху точки.
- закон
руху точки по траєкторії. Функція
має бути однозначною, неперервною і
диференційованою.
Модуль
швидкості визначається за формулою:
(вектор
спрямований за дотичною
до траєкторії у бік руху точки, а
прискорення розкладається на два
взаємно-перпендикулярних вектори
і
,
модулі яких дорівнюють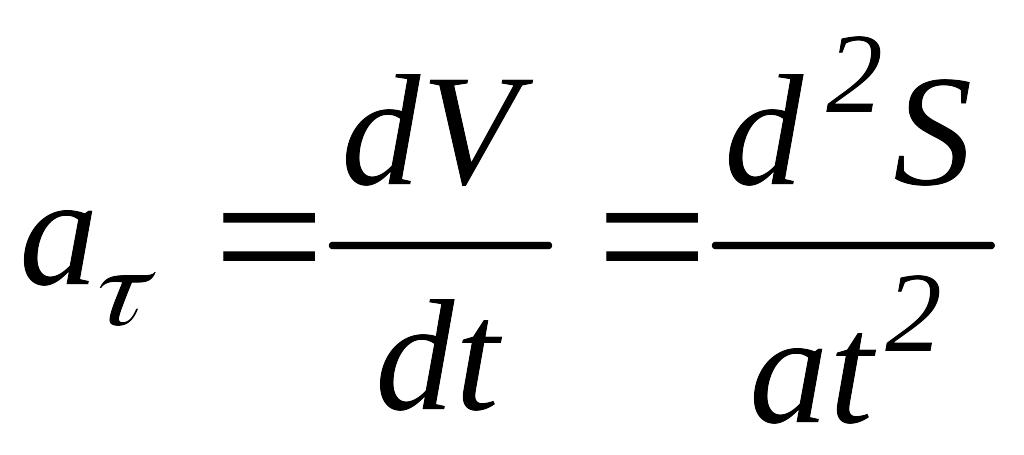
,
,
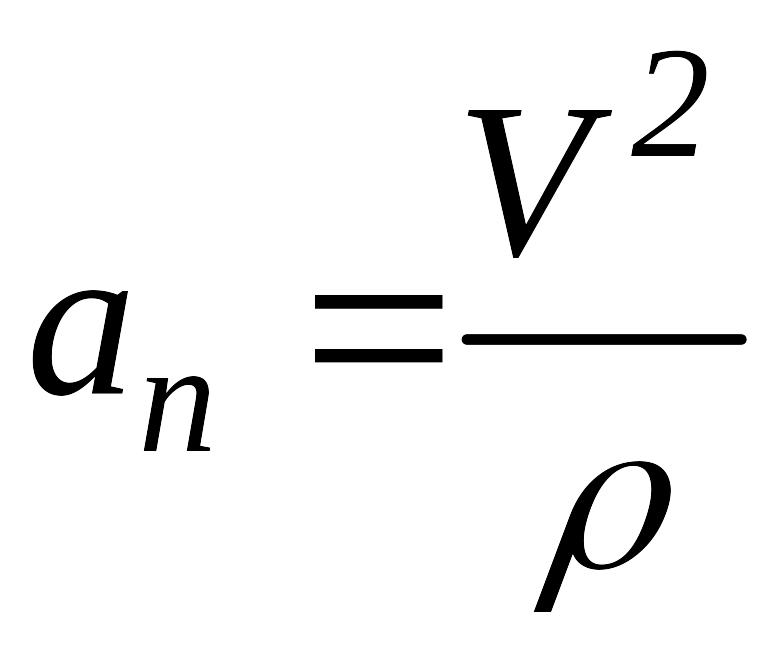де
‑
- радіус кривизни траєкторії в точці.
Якщо
,
то вектор
співпадає з напрямом вектора швидкості
або спрямований у бік, протилежний
швидкості, якщо
.
Вектор
- завжди спрямований по головній нормалі
до траєкторії точки у бік угнутості
кривої, тобто по
(рис. 4.4):
,
де
‑ орт дотичної;
‑
орт нормалі.
Модуль
прискорення
.
40Нормальне та тангенційне прискорення точки.
При
визначенні прискорення при природному
поданні руху точки, ми отримаємо рівняння
прискорення:
.
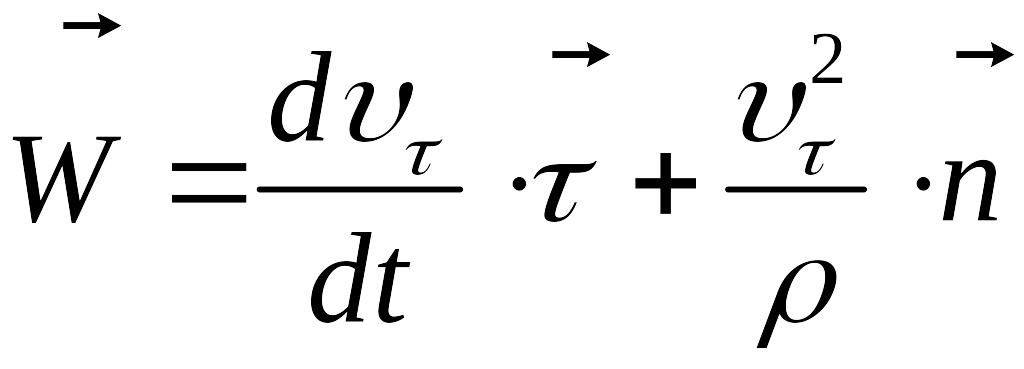Перший доданок
цього рівняння називають тангенціальним
(дотичним) прискоренням
,
а другий – нормальним
або доцентровим прискоренням
:
.
Так як орти
і
лежать в стичній площині, то і вектор
також буде лежати в цій площині. Таким
чином, повне прискорення точки в
загальному випадку криволінійного
руху:
.
Потрібно чітко
уявляти особливості кожної складової
повного прискорення. Вектор тангенціального
прискорення
напрямлений по дотичній до траєкторії
точки і характеризує зміну модуля
швидкості точки. Величина
може бути додатною, від’ємною або рівною
нулю. Вектор нормального прискорення
завжди напрямлений в бік угнутості
траєкторії і характеризує зміну вектора
швидкості точки за напрямом. Величина
завжди додатна.
Кут
відхилення вектора
від нормалі
знаходять зі співвідношення:
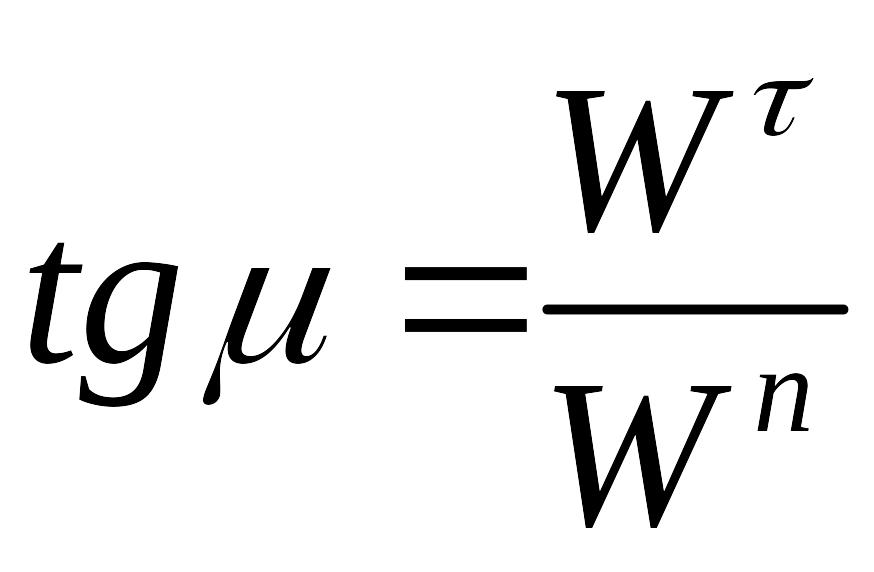
причому
.
Частинні випадки руху точки.
1.
– прямолінійний рівномірний рух.
2.
=const,
– прямолінійний рівнозмінний рух.
3.
– рівномірний рух точки вздовж
криволінійної траєкторії будь-якої
форми, або момент екстремального значення
швидкості.
4.
– рівнозмінний криволінійний рух.
5.
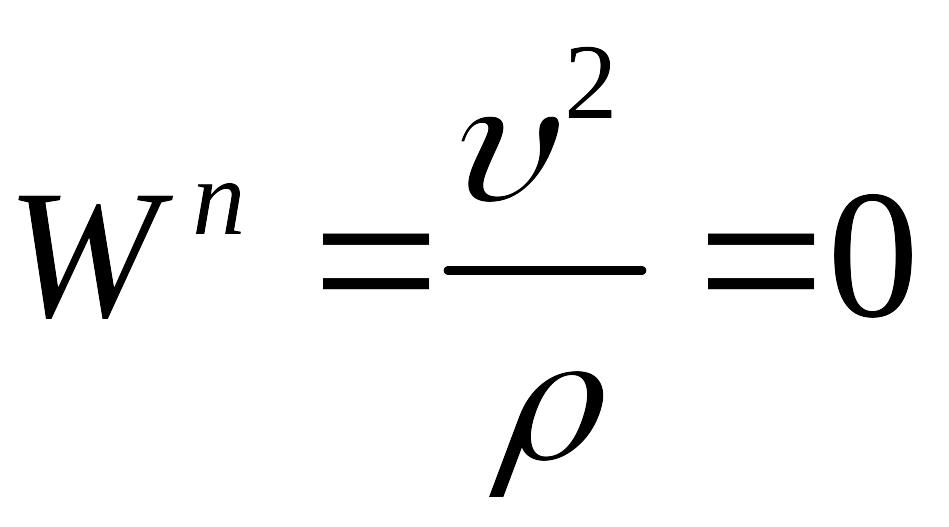– прямолінійний рух точки; момент часу,
коли рухома точка знаходиться в точці
перегину траєкторії, або моменти часу
зміни напряму руху точки вздовж
траєкторії.